Pythonで有限要素法（FEM）解析

有限要素法(FEM)を用いて1次元熱伝導方程式の近似解を求めます。FEMの計算にはpythonを使用しました。

対象とする境界値問題は、以下の定常熱伝導問題です。

【問題】
1次元の棒部材に対して、棒の左端では温度T_0が与えられ、右端ではQ_lの熱交換が行われています。また、棒の周辺では大気(温度はT_a)との熱交換が生じているとします。

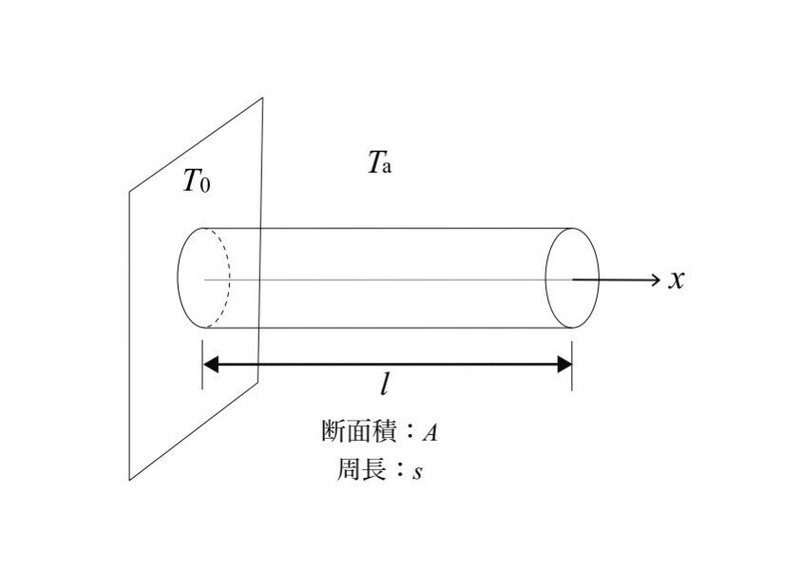
このとき、平衡方程式と境界条件は次のように書くことができます。

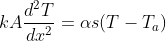
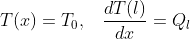
ここで、kは棒部材の熱伝導率、αは大気と棒部材間の熱伝導率です(その他の値は図の通り)。

上式について、

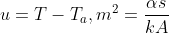
という置換を行うと方程式を単純化できます。具体的には下記のようになります。

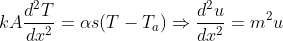
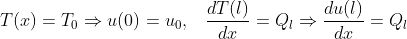
【解析解】
右端の自由端では熱交換が行われないとすると(つまりQ_l = 0)、解析解が次のように求められます。

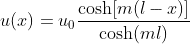
【近似解】
pythonを使って、ガラーキン有限要素法での近似解を求めます。
部材(領域)の長さはl = 1、左端のディリクレ境界条件はu_0 = 10、右端のノイマン境界条件は上記と同じくQ_l = 0とします。

例として要素数3（1次元問題なので節点数は4）での計算結果を示します。各節点の温度は、左端をu_1＠x＝0として
　[u_1  u_2  u_3  u_4] =  [10. 　7.96085048 　6.82292932 　6.45741525]
となりました。参考として、解析解を使って各節点の温度を計算すると
   [u_1  u_2  u_3  u_4] =  [10.     7.97479764      6.84391887     6.48054274]
となり、それらしい近似計算ができている？ように見えます。

【最後に】
参考文献は、森北出版の竹内則雄、樫山和男、寺田賢二郎共著「計算力学(第2版)　有限要素法の基礎」日本計算工学会編です（上記の境界値問題も文献から引用しました）。一応、計算に使用したpythonのコードも載せておきます（python初心者なので、あまり参考にならないかも。。）

【pythonサンプルコード】

""" 1次元熱伝導方程式の有限要素法 """
# 参考：計算力学-有限要素法の基礎_§5.3

import math
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

""" 計算条件の設定 """
# 計算領域
X_max = 1.0  # 最大値
X_min = 0  # 最小値
# 接点数
node_total = 4
# 境界条件
Dirichlet_U0 = 10
Neumann_xl = 0

""" 要素の準備 """
def preparation(X_min, X_max, node_total):
   # 要素数の計算
   ele_total = node_total - 1
   # 計算領域を等分割
   node_x_glo = np.linspace(X_min, X_max, node_total)
   # 各要素のGlobal節点番号
   node_num = np.empty((ele_total, 2), np.int)
   for e in range(ele_total):
       node_num[e, 0] = e
       node_num[e, 1] = e + 1
   # 各要素のLocal節点座標
   node_x_ele = np.empty((ele_total, 2), np.float)  # 各要素のLocal節点のx座標
   for e in range(ele_total):
       for j in range(2):
           node_x_ele[e, j] = node_x_glo[node_num[e, j]]
   # 各要素長さの計算
   length = np.empty((ele_total, 1), np.float)  # 各要素長さ
   for e in range(ele_total):
       length[e] = np.absolute(node_x_ele[e, 1] - node_x_ele[e, 0])

   return node_num, ele_total, length


""" 要素行列の計算 """
def Ke(ele_total, length):
   matrix_Ke1 = np.zeros((ele_total, 2, 2), np.float)
   matrix_Ke2 = np.zeros((ele_total, 2, 2), np.float)
   # 要素行列の成分計算
   for e in range(ele_total):
       for i in range(2):
           for j in range(2):
               matrix_Ke1[e, i, j] = ((-1) ** j * (-1) ** i) / length[e]
       matrix_Ke2[e, 0, 0] = length[e] / 3
       matrix_Ke2[e, 0, 1] = length[e] / 6
       matrix_Ke2[e, 1, 0] = length[e] / 6
       matrix_Ke2[e, 1, 1] = length[e] / 3

   matrix_Ke = matrix_Ke1 + matrix_Ke2
   print("要素係数行列\n", matrix_Ke)

   return matrix_Ke


""" 全体行列への組み立て """
def assemble(node_num, ele_total, matrix_Ke):
   matrix_K = np.zeros((node_total, node_total), np.float)  # 全体係数行列(ゼロで初期化)
   vector_Q = np.zeros(node_total, np.float)  # 全体係数ベクトル(ゼロで初期化)

   for e in range(ele_total):
       for i in range(2):
           for j in range(2):
               matrix_K[node_num[e, i], node_num[e, j]] += matrix_Ke[e, i, j]

   # 任意の節点に境界条件を実装する
   def boundary(node, Dirichlet, Neumann):
       # ディリクレ境界条件
       if (Dirichlet != "inf"):  # Dirichlet=無限大の時は処理しない
           vector_Q[:] -= Dirichlet * matrix_K[:, node]  # 定数ベクトルに行の値を移項
           vector_Q[node] = Dirichlet_U0  # 関数を任意の値で固定
           matrix_K[node, :] = 0.0  # 行を全て0にする
           matrix_K[:, node] = 0.0  # 列を全て0にする

       # ノイマン境界条件
       if (Neumann != "inf"):  # Neumann=無限大の時は処理しない
           vector_Q[node] = Neumann

   # 境界条件の処理
   boundary(0, Dirichlet_U0, "inf")
   boundary(node_total - 1, "inf", Neumann_xl)

   print("全体係数行列:\n", matrix_K)
   print("全体係数ベクトル\n", vector_Q)

   return matrix_K, vector_Q


""" 解を求める """
def solve(matrix_K, vector_Q, length):
   matrix_K_solve = np.zeros((node_total - 1, node_total - 1), np.float)  # 全体係数行列(ゼロで初期化)
   vector_Q_solve = np.zeros(node_total - 1, np.float)  # 全体係数ベクトル(ゼロで初期化)
   for i in range(node_total - 1):
       for j in range(node_total - 1):
           matrix_K_solve[i][j] = matrix_K[i + 1][j + 1]
       vector_Q_solve[i] = vector_Q[i + 1]

   vector_U = np.linalg.solve(matrix_K_solve, vector_Q_solve)
   vector_U_solve = np.insert(vector_U, 0, Dirichlet_U0)
   print("数値解\n", vector_U_solve)

   U = np.zeros(node_total, np.float)  # 解ベクトル(ゼロで初期化)
   for i in range(node_total):
       U[i] = Dirichlet_U0 * math.cosh((X_max - X_min) - i * length[i - 1]) / math.cosh(X_max - X_min)
   print("厳密解\n", U)

   return vector_U_solve


""" グラフの描画 """
def draw(vector_U_solve):
   array = np.array([vector_U_solve])
   plt.figure(figsize=(10, 2))
   sns.heatmap(array, cmap="Reds", vmax=10, vmin=0, yticklabels=False)
   plt.show()


def main():
   # 計算要素の準備
   node_num, ele_total, length = preparation(X_min, X_max, node_total)
   # 要素行列の作成
   matrix_Ke = Ke(ele_total, length)
   # 要素行列から全体行列への組み立て
   matrix_K, vector_Q = assemble(node_num, ele_total, matrix_Ke)
   # 求解
   vector_U_solve = solve(matrix_K, vector_Q, length)
   # 解の描画
   draw(vector_U_solve)

main()