
[ 中学の数学 ] 整数nの約数を全部足し合わせる方法
[サイトマップを見る ]
目的
2017 年,東海大学医学部の入試で次の問題が出題されました。
1680 のすべての正の約数の和を求めよ。
整数の約数の総和を求める式はあります。その式を知っておれば,この問題は確実に得点できます。なぜこうなるのか理解していないと実際の試験で公式を思い出せないということはよくあることです。この記事では,整数の約数の総和を求める方法について確実に理解できるよう説明を試みます。
準備
整数が以下のように素因数分解されるとき,
$$
n = p^a \times q^b \cdots
$$
約数の総和は次の式で計算できることを説明します。
$$
(1 + p + p^2 + p^3 + \cdots + p^a) (1 +q + q^2 + q^3 + \cdots + q^b) \cdots
$$
素因数分解 整数は素数の積で表現できます。
素因数が1つの場合
次に、数が1つの素数の積で表される場合を考えてみましょう。
$$
n = p^a
$$
n の約数の総和は次の式で求めることができます。
$$
(1 + p^1 + p^2 + p^3 + \cdots + p^a)
$$
$${8 = 2^3}$$ の場合を考えてみましょう。8 の約数の次のとおりです。
$$
1, 2^1, 2^2, 2^3
$$
全部足すと,$${1+ 2^1+ 2^2+ 2^3=15}$$ となります。
素因数が2つの場合
次に、数が2つの素数の積で表される場合を考えてみましょう。例えば、12は、12 = 2^2 × 3^1 と素因数分解できます。12の約数は、2と3の累乗を組み合わせて作ることができますね。
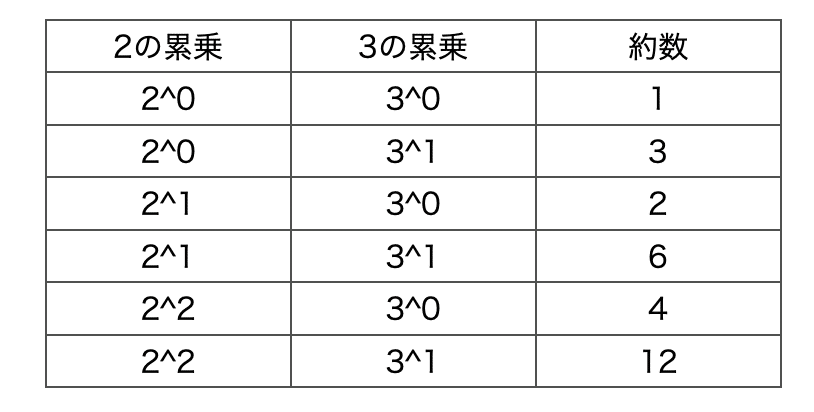
この表からわかるように、12の約数は、(2の累乗) × (3の累乗) の形で表せます。これらの約数をすべて足し合わせると、
$$
(1 + 2^1 + 2^2) \times (1 + 3^1)
$$
となります。
このように、2つの素数の積で表される数の約数の総和は、それぞれの素数の累乗の和を掛け合わせたものになることがわかります。
一般に、$${n = p^a × q^b}$$ と素因数分解されるとき、nの約数の総和は、
$${(1 + p^1 + p^2 + \cdots + p^a) \times(1 + q^1 + q^2 + \cdots + q^b)}$$と表せることが分かります。
では,具体的に$${100 = 2^2 5^2}$$ で考えてみましょう。
$$
(1 + 2^1 +2^2)(1 + 5^1 + 5^2)
$$
$$
7 \times 31 = 217
$$
簡単に求めることができます。
なぜ,このような式になるのか
なぜ,このような式になるのか考えてみましょう。続けて 100 で考えてみましょう。素因数分解すると,$${100 = 2^2 5^2}$$ です。約数は,$${1, 2^1, 2^2}$$ と $${1, 5^1, 5^2}$$の組み合わせになります。例えば,$${1 \times 1, 1\times 5^1, 1\times 5^2, 2 \times 1, 2\times 5^1, \cdots}$$ ですね。
整理すると次のように書くことができます。
$$
1 \times (1 + 5^1 + 5^2)
$$
$$
2^1 \times (1 + 5^1 + 5^2)
$$
$$
2^2 \times (1 + 5^1 + 5^2)
$$
これを足すと,次のようになります。
$$
(1 + 2^1 + 2^2)\times (1 + 5^1 + 5^2)
$$
素因数の数が3以上の場合も,同様に求めることができます。
$$
(1 + p + p^2 + p^3 + \cdots + p^a) (1 +q + q^2 + q^3 + \cdots + q^b) \cdots
$$
ところで,累乗が増えると計算する項の数も増えます。計算ミスをしやすくなりますね。今回のように累乗したものを足し合わせないで,ぱっと計算する方法もあります。それは別の記事で説明します。
より学びたい方
わたしが好きな先生です。
中学2年生くらいから読むことができます。
遠山啓「数の不思議」(SB Creative)
小学校6年生の算数の知識があれば,読み始められます。
吉田 信夫 (著)「ガウスとオイラーの整数論の世界」(技術評論社)
[ サイトマップを見る ]
この記事が気に入ったらサポートをしてみませんか?
