誕生日のパラドックス ：誕生日が一致する確率

　このパラドックスは、「何人の人を集めれば、その中に誕生日が一致する人がいる確率が50%以上になるるか?」
　という確率の問題で、その答が普通に予想されるよりも遙かに少ない、というパラドックスである（パラドックスというが論理的な矛盾があるというものではなく、単に直感に反しているというもの）。これについて紹介する。

　よく似た次の問題も考えて欲しい。「人間の髪の毛はせいぜい10～15万本と言われている。何人の人を集めれば、その中に髪の毛の本数が同じ人のいる確率が50％以上になるだろうか？」

誕生日問題の答

　この最初の問題を「誕生日問題」というが、初めて聞いた多くの人は100～200人程度の答を予想する。しかし、正しい答は「23人」である。予想と実際が大きく異なるためにパラドックスと言われ、おそらく「サンクトペテルブルグのパラドックス」や「モンティ・ホール問題」と並ぶ、確率に関する「パラドックス」である。

　実際に計算してみる。まず誕生日が同じにならない確率を求める。計算を簡単にするために、うるう年は考えないことにし、もちろん全ての誕生日は同じ確率とする。二人の場合、片方の誕生日以外の日がもう一人の誕生日であれば良いので、確率は1-1/365=364/365。3人ならば、3人目がさらに別の誕生日なら良いわけだから、(1-1/365)×(1-2/365)=(364/365)×(363/365)。以下同様にしてn人ならば、

　これを1から引けば、確率が求められる。実際真面目に計算すると、n=23のとき、

よって、

となり、確かに50%を超えている。
　（なお、うるう年で366日を考えても、50%以上になるのは同じ23人である）

　この結果はたいていの人が驚くので、確率の話のネタとして、話に興味をもってもらう導入に有用である。しかし、次のような失敗談もあるので、注意が必要である。

　数学教師；（今日から確率の章か～。学生に興味を持ってもらうように面白いネタでも話そう…）
　数学教師：さて皆、今日から確率について学んでもらおうと思うが、どうだろう、このクラスに誕生日が同じ人がいる確率はどれぐらいかと思うかな？
　学生A：う～ん、あ、いますね。
　学生B：ああ、そうだそうだ100%だよ。
　数学教師：え、なんで…
　学生C：先生、鈴木D男とE女は双子だよ。
　数学教師：ああ…orz。
　（実話らしい）

近似計算

　さて、この計算は簡単な繰り返し計算なので、表計算ソフト等で簡単に計算できるが、nを求めるのに実質的に1～nまでの全てを求めなくてはならない。nを代入しただけで、簡単に計算できるような式はないだろうか。
　というわけで次の近似式を使ってみよう。

　または、

　この近似式は、

という級数展開の最初の方の項を取り、logを外した（指数を取った）ものである。これより、

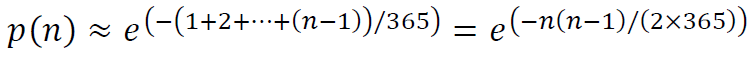
　または、

　これらを元に計算してみると、

n 　　　1-p(n)　　　  近似式(1) 　　　近似式(2)
5 　　0.027136 　　　0.027025 　　　0.027135
10  　0.116948 　　　0.115991 　　　0.116936
15  　0.252901 　　　0.249992 　　　0.252843
20  　0.411438 　　　0.405805 　　　0.411288
22  　0.475695 　　　0.468938 　　　0.475496
23  　0.507297 　　　0.500002 　　　0.507073
25  　0.568700 　　　0.560412 　　　0.568422
30  　0.706316 　　　0.696320 　　　0.705916
35  　0.814383　　　 0.804097 　　　0.813905
40  　0.891232 　　　0.881990 　　　0.890745
45  　0.940976 　　　0.933618 　　　0.940546
50  　0.970374 　　　0.965131 　　　0.970040
55  　0.986262 　　　0.982897 　　　0.986032
60  　0.994123 　　　0.992166　　　 0.993981

となる。ちなみにより大きなnで計算してみると、

70  　0.999160
80  　0.999914
90  　0.999994
100　 0.9999997
200 　0.999999999999999999999999999999998

一応グラフにしてみた。

　この「23人」という答がなぜ多くの人の感覚に合わないのかというと、恐らく無意識のうちに、「自分と同じ誕生日」をイメージし、「他人同士が同じ誕生日である可能性」を考えないからだろう。実際、「（自分を含めた）n人の部屋に自分と同じ誕生日の人がいる確率」は、

と考えられるので、n=23では約6%に過ぎない。50%以上になるのは、n=253である。

応用

　こんなパズルが何かの役に立つのか？いや、役に立つので色々研究がされている。一つの大きな応用は、コンピュータ科学に関係するものだ。

　ハッシュ関数、ハッシュ値というものがある。細かい話は省略するが、あるデータを与えたときに、そのデータ固有の値を「ラベル」として返すものだ（データをハッシュ関数に渡すと固有のハッシュ値を返す）。例えば、コンピュータプログラムを組むときに変数を定義すると、コンピュータの中でその変数に固有の番号がラベリングされる。コンピュータは数しか扱えないので、変数xに例えば”20”という数値をラベルとして与える。色々なハッシュ関数があるが、出来るだけ「固有」のラベル値を与えられなければならない。次に定義された変数yに、xと同じ”20”が与えられたら困る（こういうことが起こることを「衝突」という）。さて、ハッシュ関数の返すラベル値（ハッシュ値）をどれだけ用意すれば、衝突が起こらないか、というのが問題だ。
　おわかりだろう。「誕生日の問題」は、
・人を区別しようとラベルを365枚用意して、ランダムにラベルを貼り付けた。
・365枚も用意したら200人ぐらいはうまく区別できるだろうと考えた。
・ところが実際は10人でもラベルが重なってしまう確率が10%、23人で50％以上になってしまう。
という話なのだ。詳しくは「ハッシュ関数」等を調べて欲しい（結局説明は他人任せ）。

　最後に、冒頭に出した「人間の髪の毛はせいぜい10～15万本と言われている。何人の人を集めれば、その中に髪の毛の本数が同じ人のいる確率が50％以上になるだろうか？」という問題について。

　よくある話としては、髪の毛の本数以上の人口（10～15万人）のある市には、同じ本数の髪の毛を持った人が必ずいるはずである、というのがある（鳩の巣原理）。しかし、ここまで読んでこられた方は、50%以上になる人数はずっと少ないことが理解できるだろう。そう、500人もいれば十分なのだ。

　これは、誕生日よりずっと信じられないのではないだろうか。

(2020.8.1)