142857：巡回数のある法則について

「ある数の末尾はmである。この数にnを掛けると、結果は末尾のmを頭に移動したものになるという。この数を求めよ」　―よくある数学パズルの問題

　142857に代表される巡回数は、その性質も含めよく知られている。ここでは、よく知られていることの他に、（おそらく殆ど知られていないであろう）以下の法則を紹介する。
　ある数の末尾はmである。この数にnを掛けると、結果は末尾のmを頭に移動したものになるという。このときこの数は、分数m/(10n-1)の循環節で表される。

142857と巡回数

　まず、巡回数についてまとめておこう。142857はよく知られている巡回数の一つである。巡回数というのは、その数に別の数を掛けた結果が、元の数の並びを巡回させた数になるような数をいう。言葉だけでは分かりにくいので、142857の場合で実際の計算を示すと、

142857×1 = 142857
142857×5 = 714285
142857×4 = 571428
142857×6 = 857142
142857×2 = 285714
142857×3 = 428571

となる。
　さらに、7を掛けると999999になることや、そもそもこれは1/7=0.142857 142857…から来ていることもよく知られている。

1/7などの分数が無限循環小数になる理由

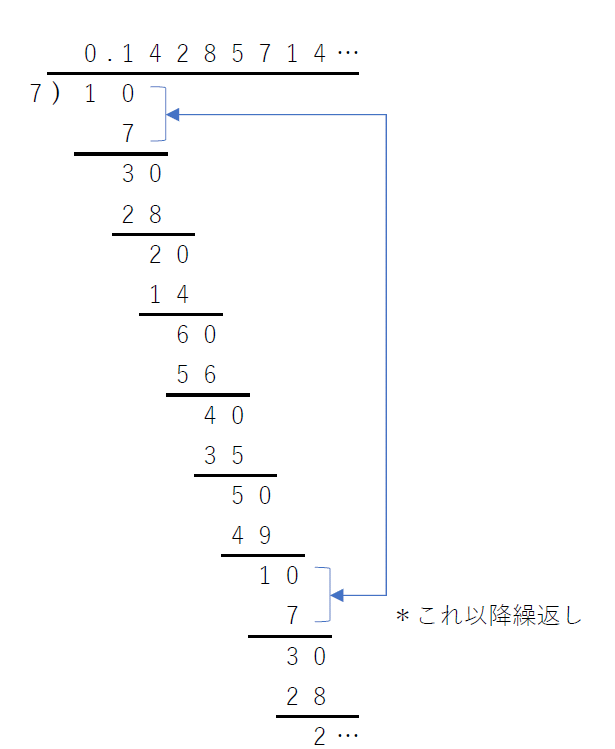
　1/7=0.142857 142857…のように、割り切れない分数を小数で表すと、結果の数字が循環する、「無限循環小数」となる。これは、下のように、筆算をしてみると明らかである。要するに、割り算をして同じ余りが出たら、後は繰り返しになる。nで割った余りはn-1種類しかない（7で割った余りは1,2,3,4,5,6の6種類しかない）ので、循環する部分（これを「循環節」という）はn-1以下の長さになる。

1/7,2/7,3/7,…などの循環節が巡回する理由

　1/7=0.142857 142857… と2/7=0.285714 285714…のように、142857と285714が巡回する（142857が巡回数である）のも、下のように筆算した結果を比べれば明らかである。要するに、同じ余りが出たら後は同じ計算となるので、当然巡回する。

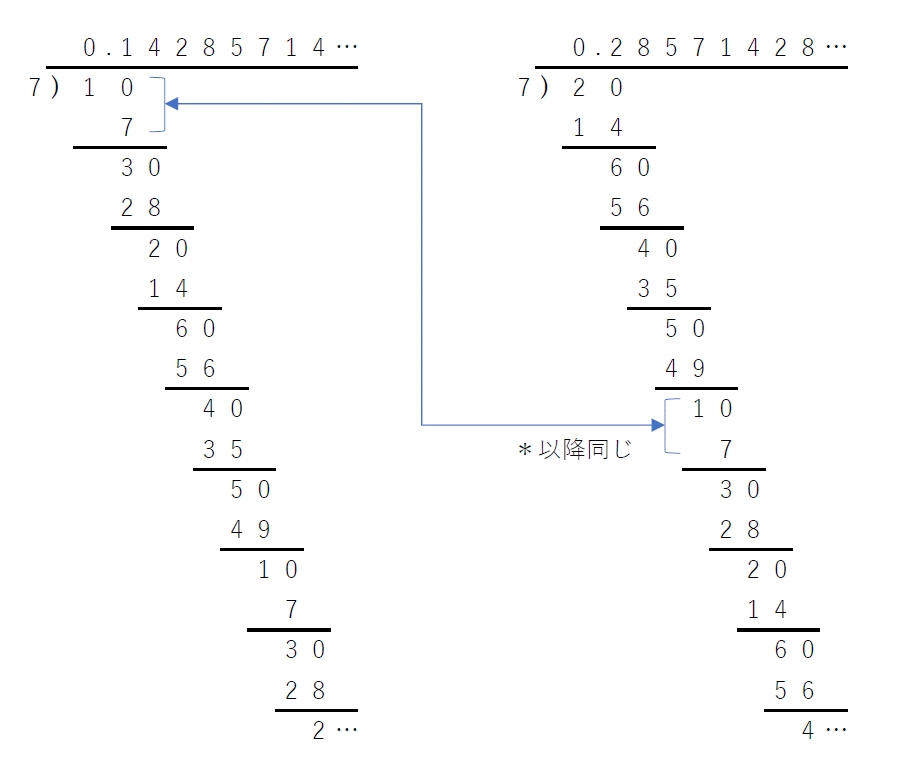
142857以外の巡回数を求める

　以上の話より、142857以外の巡回数を求めるのは簡単である。つまり、分数を計算して小数表示を求め、その循環節を取ればよい。例えば、1/17=0.0588235294117647 0588235294117647…であるので、これより、

0588235294117647× 1=0588235294117647
0588235294117647×12=7058823529411764
0588235294117647× 8=4705882352941176
0588235294117647×11=6470588235294117
0588235294117647×13=7647058823529411
0588235294117647× 3=1764705882352941
0588235294117647× 2=1176470588235294
0588235294117647× 7=4117647058823529
0588235294117647×16=9411764705882352
0588235294117647× 5=2941176470588235
0588235294117647× 9=5294117647058823
0588235294117647× 6=3529411764705882
0588235294117647× 4=2352941176470588
0588235294117647×14=8235294117647058
0588235294117647×15=8823529411764705
0588235294117647×10=5882352941176470

が求まる。

最初の数学パズルの答を求める

　実際に数学パズルを集めた本に、以下のような問題があった。

　問1：ある数の末尾は7である。この数に5を掛けると、結果は末尾の7を頭に移動したものになるという。この数を求めよ。

　今、この文章の最初の方を読めば、答は142857であることが分かる。では、以下のような問題の答をどうやって求めたらよいか。

　問2：ある数の末尾は8である。この数に4を掛けると、結果は末尾の8を頭に移動したものになるという。この数を求めよ。
　問3：ある数の末尾は9である。この数に6を掛けると、結果は末尾の9を頭に移動したものになるという。この数を求めよ。

　一つの方法は、片っ端から分数を計算して小数表示を求め、当てはまる循環節を探す方法だ。しかし、これはあまりにも効率が悪い。もし、当てはまる循環節を持つ分数が5963/9973とかであったらどうするのか。そこまでの全ての分数を計算しなければならない。
　もう一つの方法がある。問1を例に説明しよう。

　求める数は、…fedcba7である。つまり、…fedcba7×5=7…fedcba
　7×5=35であるから、a=5である。つまり、…fedcb57×5=7…fedcb5
　57×5=285であるから、b=8である。つまり、…fedc857×5=7…fedc85
　857×5=4285であるから、c=2である。つまり、…fed2857×5=7…fed285
　2857×5=14285であるから、d=4である。つまり、…fe42857×5=7…fe4285
　42857×5=214285であるから、e=1である。つまり、…f142857×5=7…f14285
　142857×5=714285であるから、f=…いやいや、既に答は求まっているじゃないか。

　途中の過程で、数字は全て一意的に決まったことに注意。要するに、問1の答になる数は本質的に142857しかない（本質的に、とわざわざ述べたのは、142857142857や142857142857142857…も答になるからだ）。
　それでは、実際に問2,3の答を求めてほしい。

最初の数学パズルの答を全て求める

　実際に計算すれば明らかであるが、一応答合わせをすると、問2の答は205128である。これは、分数では8/39= 0.205128 205128…の循環節であり、32/39= 0.820512 820512…と確かに4倍になっている。問3の答は、
1525423728813559322033898305084745762711864406779661016949であり、9/59と54/59の循環節に対応する。
　ここまで来ると、全ての場合について求めたくなる。すなわち、最初のパズルで、任意のm,n全ての答を求めたい。
　数字の末尾mは1～9の9通りしかないし、掛ける数nも2～9の8通りに限られる。10以上の数を掛けると、桁が増えてしまうからだ。さらに良く考えると、nはmより大きくはなれない。例えばm=3であれば、nを掛けて先頭が3になるのだから、元々の先頭の数字が1であっても、4以上の数を掛けたら先頭の数字が3にはならないからだ。
　さて、色々計算すると、以下のような表を作る事が出来る。

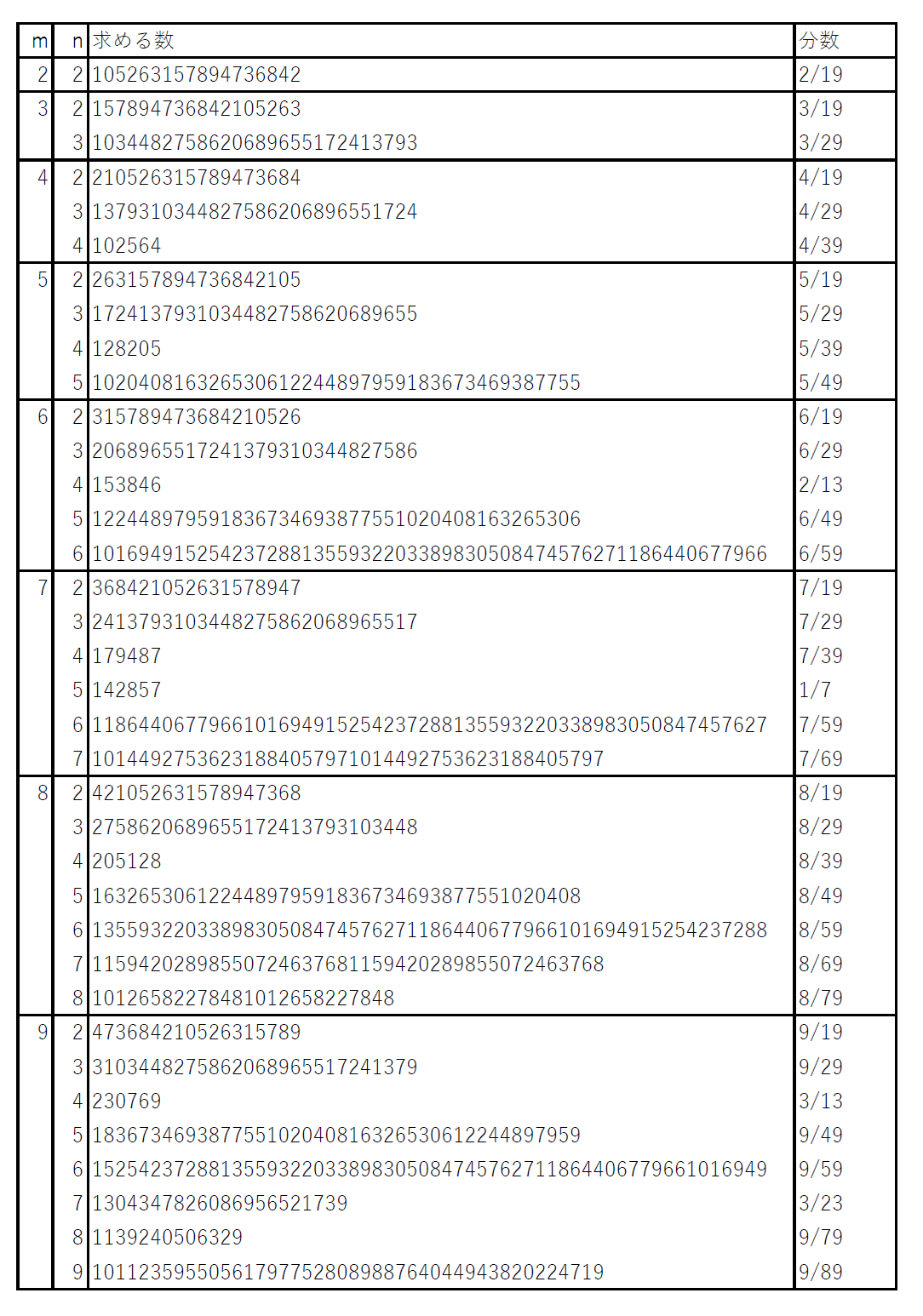
　右側の分数は、対応する循環節を持つ分数である。これをよく見てみると、あることに気が付く。例えばm=8のところの分数を見ると、8/19,8/29,8/39,…,8/79と規則的に並んでいる。mの他の場合も同様である（約分されている分数に注意）。
　これをまとめると、最初に述べた

　ある数の末尾はmである。この数にnを掛けると、結果は末尾のmを頭に移動したものになるという。このときこの数は、分数m/(10n-1)の循環節で表される。

という結果になる。

　綺麗な結果であるので既に知られていると思われるが、それに自分で気が付くか誰かに指摘されるまでは、「yoshik-yの法則」だと思っておくことにする。

(2020.2.15)