πを表す積分 ：円周率πは22/7より小さい

　定積分でπを表す式はたくさん知られている。それを元に、πの近似値を求めることや、面白い式を導くことが出来る。これについて紹介する。

よく知られている定積分

　一番よく知られているのは、次のものだろう。

　これは、

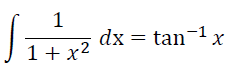
であることから明らかであるが、逆三角関数を習っていない高校数学の範囲で定積分だけは求めることが出来、練習問題として有名である。

円周率πは22/7より小さい

　この有名な積分を使った、これまた有名な話に、πが22/7より小さいことを証明できるというものがある。

　ここで、左辺の積分の値は、積分区間内で分母も分子も0以上なので0より大きい。従って右辺も0以上であるから、22/7がπより大きいことが示される。

　これを実際に計算するには、普通に左辺を展開すれば良く、

　であるから、これを分母で割って、

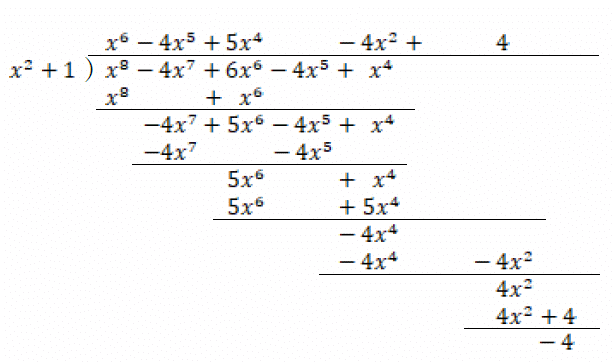
なので、

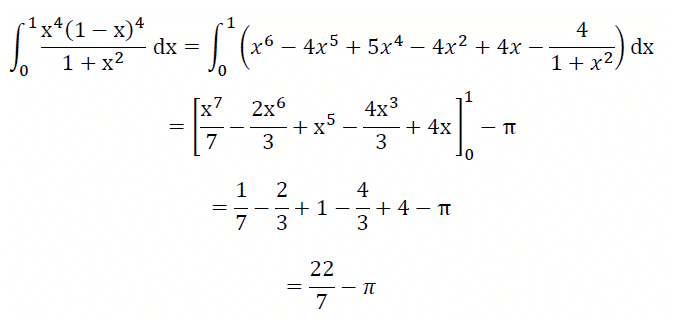
はすぐに計算できる。

分子を変えた場合

　こうなると、分子を変えるとどうなるか試してみたくなるのは当然である。試しにxの4乗ではなく3乗にしてみると、

となってしまい、πが出てこない。もちろん、

なので、πの代わりにlog 2を表す積分の話が出来る訳であるが、殆どの人はπに興味があってもlog 2に興味はないだろう。
　それでは、単純にxの2乗ではどうか。計算してみると、

となり、これから分かるのは、「πは4より小さい」ということで、あまり面白くない。

ここまでをまとめると

　まとめると、以下のようになる。

　適当なxの多項式f(x)で、以下のような定積分を計算する。

　ここで、次の場合にπの近似値を求めることが出来る。
　①左辺の定積分の値が、正か負か簡単に判断できること（これで求めた値とπの大小が分かる）
　②A=0であること
　③（より良い近似のためには）定積分の値が0に近いこと

　こう考えると、πが22/7より小さいことを証明するために使ったf(x)は良く出来ている。①,②を満たすだけでなく、xが0→1に動くとき、xの4乗の項と(1-x)の4乗の項は、それぞれ0→1と1→0のように反対向きに動き、掛け合わせた結果が0に近いことから、結果として定積分の値を0に近くするからである。

4乗以外の場合

　乗数を上げていけば、定積分の値が0に近づいていくのは明らかなので、より良い近似値が得られるはずである。以下に0乗から10乗までの計算結果を載せる（途中までは手計算で確かめたが、後はwxMaximaに頼った）。m,nの値が飛び飛びなのは、例によってlog 2が出てくるからだ。殆どの人はπに興味があってもlog 2に興味は…（以下略）。これで、例えば「πが3.05より大きいことを証明せよ」という有名な問題には、m=5,n=2について、前述の22/7のように証明すれば良いことが言える。

xのn乗からライプニッツの公式が得られる

　手計算でないと見落とすこともある。xの2乗を分子にし、あまり良い結果が得られないことを前述した。表を見ても、10乗でもπ<3.339683…としか言えない。だがちまちまと手計算してみると、

　以下同様にして、有名なライプニッツの公式

が得られる。ちなみに、分子をxの奇数乗にすると、これまた有名な式

が得られるが、殆どの人はπに興味があってもlog 2に興味は…（以下略）。

　家に籠もって暇なときは、分子f(x)に色々な式を入れて計算してみると、色々な発見があるかも知れない。

（2020.7.27）