円周率πを内接(外接)する正多角形から求める

　あまりにも有名なネタであるが、数ネタとして一度は取り上げておいた方が良いとの考えから一応まとめておく。
　なお、正方形または正六角形を元に角を二等分することを繰り返す、というこの方法で、三角関数の所謂「半角公式」を使うのが正解のように言われている。「円周率πを内接(外接)する正多角形の辺の長さより求めよ」という問題なら、三角関数でも何でも自由に使えば良いと思うが、「円周率πを求めよ」というような方法が指定されていない問題の場合、もし三角関数の半角公式を使うのなら、内接(外接)多角形を持ち出す必要はないことに注意すべきである。
　このことは、後述する。今回、基本的には初等幾何を使う。

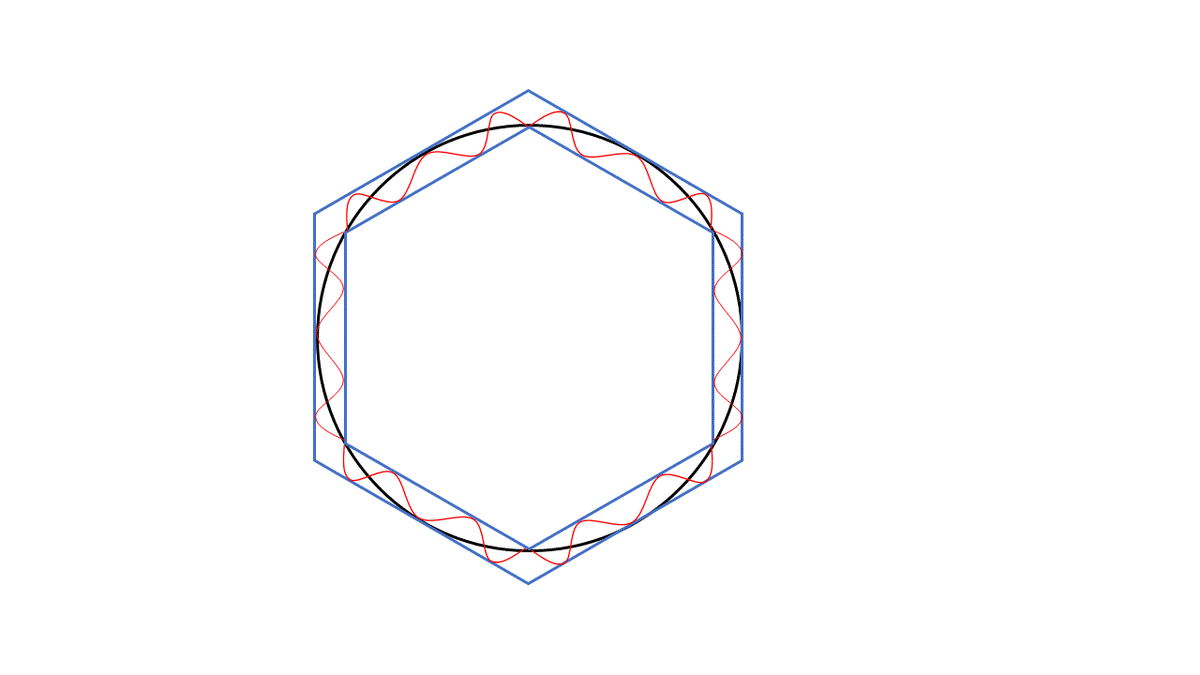
内接正多角形と外接正多角形で円を挟む

　下図のような感じで、外接正多角形と内接正多角形で円を「挟む」と、
内接正多角形の周の長さ＜円の周の長さ＜外接正多角形の周の長さ
であるから、それぞれの正多角形の辺の長さを円の半径で表すことが出来れば、…

　いや、ちょっと待って欲しい。内接多角形は良い。頂点と頂点を直線で結んでいる内接多角形の周の長さが、曲線で結んでいる円周より小さいのはまあ明らかだ。しかし、外接多角形の辺が円周より大きいかどうかは微妙で証明がいるのではないか？極端な話、下の図の赤い曲線だったらどうだ？内側だから短いとは言えないのではないか？

　これは、以下のように線を引いてみれば、0<θ<π/2において、sinθ<θ＜tanθか？という問いに等しい。もちろん、微積分をある程度習って曲線の長さが求められるようになれば証明できる。しかし、微積分の導入時に証明なくsinθ<θ＜tanθとしてしまったり、証明にならない循環論法でごまかしてしまったりする場合が多い。これを嫌って内接正多角形のみで議論しπの下限値のみ求める場合や、辺の長さでなく面積で比較する、等の方法が採られることも多い。

　今回は、いちゃもんを付けず「内接正多角形の周の長さ＜円の周の長さ＜外接正多角形の周の長さ」を認めて、話を進めよう。

内接正多角形の辺の長さを求める

　半径1の円Oに内接する正n角形の辺の長さをaとしたとき、同じ円に内接する正2n角形の辺の長さa’を求める。

　この式を繰り返し使うことで、正n角形より始めて、正2n,4n,8n,…角形の辺の長さが求められる。試しに正四角形(正方形)より始めると、正方形の1辺の長さは√2。以下、正n角形の辺の長さをa(n)で表すと、

となる。

なので、

これを64倍すると6.280662313909…より、円周率πの近似値として3.140331156…を得る。

外接正多角形の辺の長さを求める

　半径1の円Oに内接する正n角形の辺の長さをaとしたとき、同じ円に外接する正n角形の辺の長さbを求める。

AB=a, CD=b である。

　これで、外接多角形の辺も計算できるようになった。先ほどの内接正64角形の辺の長さa(64)より、外接正64角形の辺の長さb(64)を求めると、

となり、これを64倍すると6.288236770491…より、円周率πの近似値として3.144118385…を得る。
　まとめると、

で、円周率πが3.14…であることが示された。

アルキメデスの方法

　教科書等には同様の方法でアルキメデスが正96角形を使ってπ=3.14…を求めたと書いてある。これを確かめてみよう。
　96=6×16(2の4乗)なので、アルキメデスは正6角形から始めたことが分かる。上記の方法でも同じように求められるが、アルキメデスは上記の式をさらに変形し、内接正多角形と外接正多角形の辺の長さを同時に求める「巧妙な」方法を使ったといわれている。以下のようである。

　円に内接する正n角形の周囲の長さをp、外接する正n角形の周囲の長さをPとし、正2n角形の周囲の長さをそれぞれp‘、P’とする。そのとき、

が成り立つ。

　実際に計算してみれば分かるが、先ほどの内接正多角形の辺だけを求めておいて、後から外接正多角形の辺を求める方法に比べて、楽にはならない(「巧妙」ではあるが)。この式の優れている点は、P’がpとPの調和平均、p’はｐとP‘の幾何平均になることを示したところにある。古代ギリシャでは、現在良く知られている算術平均、幾何平均、調和平均の他にさらに7つの平均が定義されており、平均の概念は重要な物であった。

　余計な蘊蓄は置いておいて、この式で実際に計算してみよう。内接正n角形の周囲の長さをp(n)、外接正n角形の周囲の長さをP(n)とする。正6角形からスタートすると、p(6)=3は明らかだが、P(6)は上記の「外接正多角形の辺の長さを求める」から求める必要があり、これは

2/√3=2√3/3(=3.4641016…)。以下は次々に求められる。
p(6)=3　　　　　　  　 P(6)＝3.46410161…
p(12)=3.10582854…　  P(12)=3.21539030…
p(24)=3.13262861…　  P(24)=3.15965994…
p(48)=3.13935020…　  P(48)=3.14608621…
p(96)=3.14103195… 　P(96)=3.14271460…

であるので、アルキメデスが求めたとよく言われている、

が示された。
　(参考：上式は漸化式として簡単にパソコンでプログラムできる。参考に正6291456(6*2^20)角形で計算すると、p(6291456)= 3.1415926535896…、P(6291456)= 3.1415926535900…と小数点以下10桁まで確定する)

　アルキメデスの時代にはまだ小数表記が使えなかったため、計算は全て分数で行われた(だから結果も小数でなく分数になっている)。平方根の計算も分数近似に依っていたので、計算は極めて大変だったはずだ。

三角関数の使用について

　最初に「πを求める方法が指定されていない問題の場合、もし三角関数の半角公式を使うのなら、内接(外接)多角形を持ち出す必要はない」と述べた。誤解されないように強調しておくが、三角関数を使うなと言っているわけではない。上記の円に内接(外接)する辺や周囲の長さを求めるのに初等幾何の方法を使ったが、三角関数を使う方が分かりやすかったら使えば良い。分数を使うのが大変だったら小数を使えば良いのと同じことだ。言いたいのは、三角関数を使うならもっと巧く使えということだ。以下のような例題を考えてみよう。

　例題）円周率πが、3.05<π<3.25であることを証明せよ。

　三角関数を使えないのなら、上記の円に内接(外接)する辺や周囲の長さを求める方法で解いても良いだろう。しかし、そこで三角関数の半角公式等が使えるのなら、最初から、

として、

よりいきなり半角の公式を使えば良い。
　もしろん、これは内接・外接正6角形の辺の長さの計算と計算自体は等しい。しかし、円や多角形を持ち出す必要はなくなる。三角関数を導入するときは三角形や単位円が必要となるが、微積分まで進んだときには図形から離れた1つの「関数」として、その性質だけを使って良いわけだ。

(2021.6.20)