コインを投げて円周率πを求める：表の出たコインの枚数を数えることで円周率πを求める

　良く分からない関数の計算とかではなく、物理的に円周率πを求める方法は数多く知られている。もちろん、円を描いて実測するのもそれと言えるが、振り子の周期を測ったり(注1)、2つの玉を壁にぶつけたり(注2)、的にダーツを投げたり(注3)…と色々だ。
　特に物を投げることでπを求める方法としては「ビュフォンの針」(注4)が有名だが、線と針が交差しているかどうか判断に困る場合があることや、針で怪我をしてしまうなどの問題がある。
　ここでは、コインを投げ、表の出た回数を数えるだけで、円周率πを求める方法について述べる。

　(注1)振り子の周期T、糸の長さL、重力加速度Gから、π=(T/2)×√(G/L)。
　(注2)壁、玉1、玉2と直線上に並べ、玉2を玉1にぶつけたとき、玉1が玉2及び壁にぶつかる回数をnとすると、π=n/√(玉2の質量/玉1の質量)。
　(注3)正方形とそれに内接する円を描き、的とする。適当に投げたダーツが正方形内に命中したとき、その中のさらに円内に当たる確率はπ/4。
　(注4)床に針の長さの2倍の間隔で並行に線を描く。n回針を床に投げ、そのうちm回針が線と交わったとすると、π=n/m。

やり方

　まず、やり方を説明しよう。
　(1)コインをn回投げ、表の出た回数を数える。
　(2)(1)を1セットとし、A回セット繰り返す。表の出た回数がちょうど半分のn/2回であったセット数Bを数える。
　(3)π=2×{(A/B)の2乗}/n　でπを求める。

　n，Aが大きいほど真の値に近づく。やってみよう。コインを何回も投げるのが大変だと言う人もいるかも知れないが、お金持ちなら一度にn枚投げてもかまわない。

実際にやってみた結果

　実際にやってみようと思ったが、時間もコインもないので(財布の中は万札ばかり)、パソコンでプログラムを組んでやってみた。コードをエラそうに書くほどの物ではない。あらかじめ用意されている関数で0～1の乱数を発生させ、0.5未満なら裏、0.5以上なら表が出たことにし、上のやり方通りの計算をさせるだけだ。
　n=100、A=10000で3回やってみたのが下のグラフだ。横軸はAで縦軸が計算されたπだ。

　1つの線で100万回、全部で300万回コインを投げているが、これは酷い。100万回投げて、「πはほぼ3」の結論でしかない(ちなみにそれぞれの値は、3.278898159、3.417489000、2.981687963)。
　A=100000でやってみたのが次のグラフだ。3.1133141268と、さすがにましな結果が出ているように見えるが、下の拡大したグラフを見れば分かるように、まだまだπ=3.1415926535…に収束するようには見えない。1000万回コインを投げて、この結果というのは、やはりお金に頼るのは良くないということかも知れない。

　コイン以外の物を使わないでπが求められないだろうか、と考えたのが今回の話だが、まあ求められなくもないけど…という結果だった。では、何故この方法でπが求められるのかを書いていこう。

コインの表裏と二項分布

　二項分布というと、あれだ。そう、パスカルの三角形だ。

　作り方も有名で、まず最上段に1を置き、それより下の段は両端には1、それ以外の場所には右上の数と左上の数の和を置けば良い。
　これは良く二項係数を求めるときに使用され、例えば

のそれぞれの係数は三角形の3段目の数121と一致する。同様に例えば、

のそれぞれの係数は三角形の5段目の数14641と一致する。

　さて、コインとの関係だが、コインをn回投げたときの表裏の出方の数が、n+1段目の数と一致している。例えば、コインを2回投げたときの表裏の出方を表○、裏●で示すと、
表2枚：○○　　　　1通り
表1枚：○●　●○　2通り
表0枚：●●　　　　1通り
で、3段目の数121と一致する。10回投げたときは11段目を見れば良い。これはもちろん表の出る確率も表しているのであって、n段目の数の合計は(n-1)の2乗であるので、例えば、コインを10回投げたときに表が5回出る確率は、252/1024であることが分かる。
　じゃあ100回投げて50回表が出る確率は101段目の真ん中(51番目)を見れば良いわけだが、三角形をそこまで作るのは面倒くさい。いきなりn+1段目のr+1番目(つまりn回投げてr回表が出る組み合わせの数)を表す式があって、それは

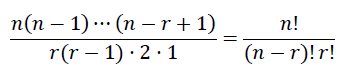
となる。確率を求めるにはこれを2のn乗で割れば良い。最初の「やり方」にあった(A/B)は、この確率(の逆数)を求めていたわけだ。

二項分布と正規分布の関係

　二項分布や最初の「やり方」のA/Bは分かった。しかし、肝心のπがまだ出てこない。それについて説明しよう。二項「分布」がどのような分布かは、実際にグラフを描いてみれば分かる。例えば、パスカルの三角形の11段目(コインを10回投げた場合)でプロットすると、下図のようになる。

　左右対称の綺麗な釣り鐘型であるが、n数を増やすとどんどんなめらかな曲線に近づく。さあ、どんな曲線に近づくか、ということを実際にコインを投げて研究した数学者がいる。ド・モアブル(「ド・モアブルの定理」で有名)だ。彼は、数千回コインを投げることによってこの曲線、すなわちn回コインを投げるときにm回表が出る確率p(m)が以下の式で表されることを見いだした(話の都合上、多少式を変えているが同じ内容である)。

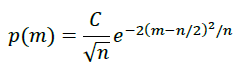
　パソコンを頼りに100回コインを投げるのも苦労している輩とはえらい違いだ。しかし、定数Cがどのような値になるかは分からなかったようである。定数Cを求めたのは友人のスターリング(彼もまた「スターリングの公式」で有名)で、先ほどの式は以下のようになる。

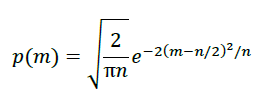
　これは全く正規分布の式で、今回の話のネタばらしをすると「正規分布の式にπが入っているけど、ここからπを求められないかな」と思ったのが始まりだ。eの項が邪魔で、πを求めるのにeの値が必要になると面白くないので、m=n/2としてしまえば、eの0乗=1となりeの項を消し、

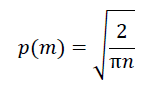
と出来るわけだ。これが「やり方」の(3)になる。
　現在では、「二項分布は中心極限定理によって正規分布に近似できる」とあっさり言えるが、ド・モアブルがコインを投げていたときには、まだガウスは生まれていなかったし、正規分布の概念もなかった。従って二項分布に限っては、特別に「ド・モアブル=ラプラスの定理」と名前が付いている。
(終わり)

説明の終わりの後の余計な話

　さて、前節で終わってもそれなりに纏まっていたので良かったのだが、ろくでもないことに気が付いてしまったので、それについて書くことにする。
　最初のコイン投げのシミュレーションで、なかなか値が収束しなかったのは、コインを100回投げて50回表が出る確率を「実際に投げることによって(シミュレーションだが)」求めていたからだ。しかし、この確率は「コインの表裏と二項分布」で述べたように次式で計算できる。

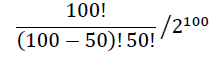
　これで得られた値を使って、「やり方」の(3)の通りの計算で本当にπの値になるだろうか？というのが気が付いてしまったことだ。二項分布は確かに正規分布で近似できる。しかし、この近似精度が悪ければπに収束しないのでは？
　計算してみた。

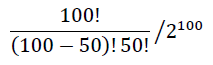
=100891344545564193334812497256/1267650600228229401496703205376
=0.07958923738717876…
「やり方」の(3)の通り、この数の逆数を取って2乗して100で割って2を掛けると、
=3.157339689217565…
…。3.14…にならない。近似が甘かった。

　これを解決するには、コインを投げる回数ｎを増やすしかない。100回投げて50回表が出る確率ではなく、1000回投げて500回表が出る確率を求めるようにしたらどうだろうか。計算してみると、

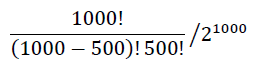
=4223253764772446398681479587905863679627375131977316984490513673541022323523784279665820061320349533833790720078461657887534527344541873711717097182804976178494773191621120833690038501245904489755696471267492150071422577902441998133040640534678543005733060259424013478163819189207764154121872206505
/167423219872854268898191413915625282900219501828989626163085998182867351738271269139562246689952477832436667643367679191435491450889424069312259024604665231311477621481628609147204290704099549091843034096141351171618467832303105743111961624157454108040174944963852221369694216119572256044331338563584
=0.0252250181783608…
なので、同様に逆数を取って2乗して1000で割って2を掛けると、
= 3.143163842419198…

　なんとか3.14…になった。セット数Aを先と同じ100000にした場合、1億回コインを投げる必要があるが、そのままでは1000回投げて500回表が出る確率が収束しないと思われるので、もっとセット数を増やす必要がある(確率が少ないので、それを精度良く求めるにはより回数が必要と予想できる)。
　恐らく、100億回ぐらいコインを投げないと3.14に収束するところは見られないのではないだろうか。

　今回は、挫折してしまった。誰か100億回ぐらいコインを投げて確かめてくれないだろうか。

(2021.6.8)