
圏論ノート:モナド
モナドについてちょっとわかった気がしたので、モナドの話をします。
Monoidal Category
まず Monoidal Categoryの話をします。日本語でなんていうんだ。
Monoidal CategoryはカテゴリーCでユニット Iというオブジェクトと⊗ : C×C→Cというbifunctorを持つものです。⊗は次の自然な同型を持たなくてはいけません。

⊗が結合則を満たすこととIが単位元であることを言っています。また、次の図式が可換でなければなりません。

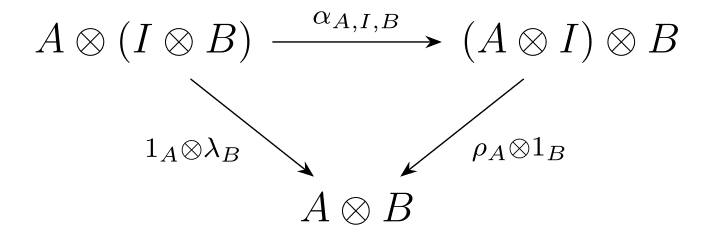
(Wikipediaより)
まあ成り立っていて欲しいことが成り立っていて欲しいということです。(成り立たない例はあると思いますが知りません。)
モノイドっぽいな、と思うと思います。
モノイドオブジェクト
Monidal Categoryの中にモノイドオブジェクトというものが定義できます。モノイドオブジェクトは「掛け算」μ : M × M → Mと「ユニット」η : I → Mで次の花冠図式を満たすものです。図式を書くのが面倒なので、またWikipediaからの引用です。


モナド
やっとモナドにたどり着きました。モナドはあるカテゴリーCの自分自身への関手全体End(C)の中のモノイドオブジェクトです。End(C)のオブジェクトはCからCへの関手、射は自然変換です。End(C)は関手の合成を積、恒等変換I:F→FをユニットとしてMonoidal Categoryになります。モナドTはこのEnd(C)の中のモノイドオブジェクトです。つまり、掛け算μ : T ◦ T → Tとユニットη : I → Tを持ち、
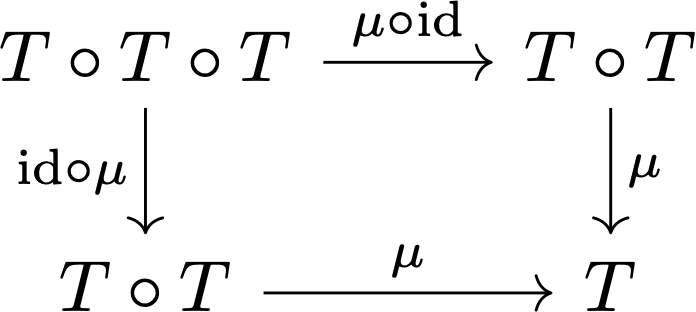

射の言葉で書き直すと、普通のモナド則が得られました。
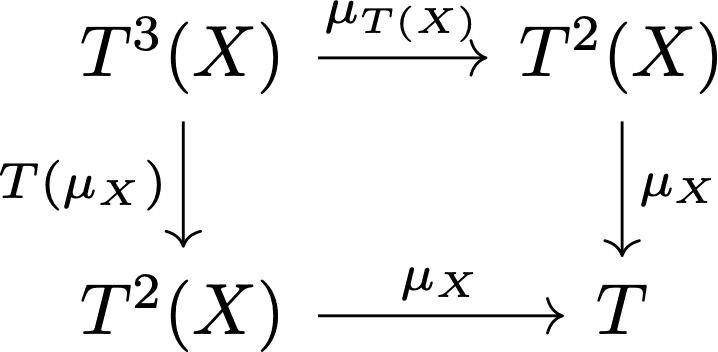

モナドの具体例はネットにたくさんあるので特に書きません。
まとめ
Monoidal Categoryのモナドオブジェクトの一例としてモナドを導きました。
