
Googleの新サービス『NotebookLM』とは?基本的な使い方と、できること・できないことを解説
Googleの新サービス「NotebookLM」が日本でサービスを開始しました。ドキュメントベースでGeminiを活用できるサービスで、ドキュメントの一部を指定し、その部分に関する補足説明や追加アイデアを得たり、得られた知見をメモに残したり出来ます。
今回は、NotebookLMの基本的な使い方と、応用例を解説したいと思います。
ソースのアップロード
NotebookLMには、「ソース」というGeminiとの対話対象のドキュメント元になるテキストやPDFをアップロードする機能があります。ソースのアップロード方法は、以下の5種類から選択できます。
Googleドライブ
Google DocやSlideをアップロード可能
PDF
テキストファイル
コピーされたテキスト
ウェブサイト

ここからアップロードされたソースを基にGeminiと対話していきます。ソースは複数個アップロードでき、選択したソースに対して対話することができます。

基本的な使い方
対象ソースとの対話
選択したソースを基に、下部に表示されているチャットで対話することができます。

試しにマッキンゼーの資料「学校現場での「主体的・対話的で深い学び」の実践を加速させるために」のPDFをソースとして対話してみます。
ソースを開くと、上部に概要、下部にPDFの全文が表示されます。

チャットボックスには、質問例が表示されます。試しに「日本の学校教育において「主体的・対話的で深い学び」が導入された背景は何ですか。」という質問を投げてみます。

すると、ソースの情報を基に質問に回答してくれます。

NotebookLMの素晴らしい点は、この回答に引用元が記されていることです。引用番号にマウスを合わせると、引用元が表示されます。また、クリックすると、左下部に表示されるソース内容が自動的に引用元の箇所に移動します。
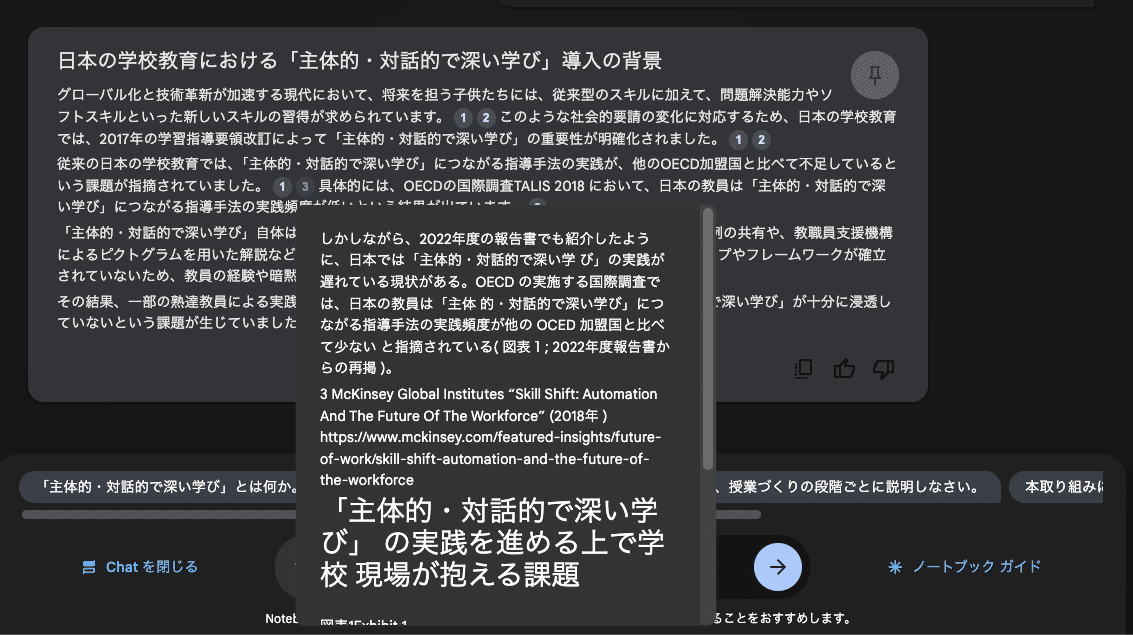
その他に、ソースの中で理解ができない箇所を説明してもらうこともできます。例えば、ソースに「アクティブ・ラーニング」という言葉が出てきますが、この言葉の意味を理解したいとします。その場合、ソースの「アクティブ・ラーニング」を選択することで、選択したテキストに対して対話が可能となります。テキストを選択すると、チャットボックスには、関連するアイデアを提案、メモに要約、メモに追加、理解をサポートの4つのよく使われるであろう質問が表示されます。もちろん、この質問以外に、チャットボックスに入力することで、独自の質問をすることが可能です。ここでは、理解をサポートを選択してみます。

すると、アクティブ・ラーニングに関する補足説明が出力されます。このように、ドキュメントとインタラクティブな要素が加わり、アクティブに読み進めることができます。

応用例
応用した使い方を考える際は、以下のGeminiの特徴を考慮すると良いでしょう。
大量の文章を読み込める
ソースの中の画像も理解できる
複数のソースを絡めて思考できる
上記の特徴を考慮して、いくつか応用例を述べたいと思います。
プレゼンテーション資料から想定問答を作成する
プレゼンテーション資料をソースに読み込ませ、その内容に関してFAQを作成してもらうことで、想定問答を他者の目線で行うことができます。
試しに「ウォンテッドリーでのKMPワークフロー」に対して、FAQを作成してみます。(ネットで公開されていたので試しに使いました)
ノートブックガイドにある「FAQ」をクリックします。

資料からFAQを作成した結果が以下になります(少し長いですが全文貼り付けます)。これだけ詳細なFAQを作成できるので、プレゼンにも万全な準備で臨めるでしょう。
Q1: KMP導入のメリットは何ですか?
A1: KMP導入の主なメリットは、iOSとAndroidの両プラットフォームでコードを共有できるようになり、開発効率とコードの品質が向上することです。 これにより、開発時間の短縮、バグの減少、一貫性のあるユーザーエクスペリエンスの提供が可能になります。
Q2: KMPチームの構成はどうなっていますか?
A2: KMPチームは、専門性を持ったiOSエンジニアとAndroidエンジニアで構成されています。開発は、共通のKMPインターフェースを軸に進められ、iOS、Androidそれぞれのエンジニアが自身の専門性を活かしながら開発を進めています。
Q3: ウォンテッドリーのKMPワークフローの特徴は何ですか?
A3: ウォンテッドリーのKMPワークフローは、「設計重視」「フィードバック重視」「CI/CD活用」の3つを特徴としています。
設計重視: 手戻りを減らすため、StateとActionをモデリングし、KMP/iOS/Android全エンジニアがレビューすることで、設計の質を高めています。
フィードバック重視: 結合時の課題を早期に発見・解決するため、結合工程を分離せず、グラデーションのように徐々に結合を進めながら、随時フィードバックを交換しています。
CI/CD活用: メインブランチへのマージをトリガーに、自動的にiOS/Android側へのPRが作成されるCI/CD環境を構築。結合の手間を減らし、迅速なフィードバックを実現しています。
Q4: 開発ワークフローにおける各工程の役割は?
A4: 開発ワークフローは、大きく分けて「KMPインターフェース設計・実装」「KMP内部実装」「iOS UI実装」「Android UI実装」「結合」の5つの工程からなります。
KMPインターフェース設計・実装: StateとActionを定義し、KMP/iOS/Androidの全エンジニアがレビューすることで、設計の質を高めます。
KMP内部実装: 定義されたStateとActionに基づき、KMPの内部実装を進めます。
iOS UI実装: KMPのStateを参照し、SwiftUIなどを用いてiOS UIを実装します。
Android UI実装: KMPのStateを参照し、Jetpack Composeなどを用いてAndroid UIを実装します。
結合: KMPの内部実装が完了したら、iOS/Androidと結合し、動作確認を行います。
Q5: KMPインターフェース設計で重要視していることは何ですか?
A5: KMPインターフェース設計では、手戻りを減らすために、仕様整理、設計レベルの向上を重視しています。具体的には、 data class から sealed class への移行など、モデリング手法についても議論を重ね、堅牢な設計を目指しています。
Q6: 結合を効率化するためにどのような取り組みをしていますか?
A6: 以前は手動でバージョン管理・パッケージ化を行っていましたが、現在はCI/CDを導入し、メインブランチへのマージをトリガーに自動的にiOS/Android側のPRが作成されるようにしています。これにより、結合の手間を大幅に削減し、迅速なフィードバックを可能にしています。
Q7: チーム内のコミュニケーションを円滑にするための工夫はありますか?
A7: 朝会での相談や、結合時のフィードバック機会を増やすことで、チーム内のコミュニケーションを活発化させています。
Q8: 今後の課題は?
A8: 設計レベルの向上やCI/CDの活用により、開発効率は向上しましたが、更なる改善の余地があります。例えば、モデリング手法の改善や、CI/CDの適用範囲拡大などを検討しています。
教科書を読み込ませて問題を生成してもらう
教科書から問題を作成してもらえます。ネットに落ちていた英語の数学の教科書を読み込ませて、そこから問題を作成してもらいます。
https://www.ulm.edu.pk/departments/admin/upload/downloads/202110030921.pdf
ノートブックガイドから「Study Guide」をクリックします。

数問ですが、以下のように問題が生成されます。PDFの文章量に対して、問題数が少ない点が気になりますが、問題自体は生成に成功しています。
復習問題
これらの質問に、独自の学習に基づいて、それぞれ2~3文で答えてください。
1. 整数の加算における可換の法則と結合法則を説明しなさい。
2. 整数の乗算における分配法則とは何か。
3. 正の整数 m と n が与えられたとき、am * an = am+nを証明しなさい。
4. 整数の可分性とは何か、例を挙げて説明しなさい。
5. 有理数を、分子と分母に整数を持つ分数として定義しなさい。分母がゼロであってはならない理由を説明しなさい。
6. 分数の足し算の公式を書き、簡単な例を挙げなさい。
7. 有理数の乗算逆数の定義を書きなさい。どの有理数が乗算逆数を持たないか。
8. 2つの未知数を含む連立一次方程式を解くための2つの方法を説明しなさい。
9. 方程式が実数の解を持たない場合の例を挙げなさい。
10. 正の数aのn乗根の定義を書きなさい。
解答例
1. 加算の可換法則は、2つの整数の和がそれらの加算の順序に依存しないことを示しています。つまり、任意の2つの整数aとbについて、a + b = b + aとなります。結合法則は、3つ以上の整数の加算を行う場合、括弧の位置は和に影響を与えないことを示しています。つまり、任意の3つの整数a、b、cについて、(a + b) + c = a + (b + c)となります。
2. 乗算の分配法則は、ある数を2つ以上の数の和に掛けたものは、その数をそれぞれ個別に掛けてから足したものと等しいことを示しています。つまり、任意の3つの数a、b、cについて、a(b + c) = ab + acとなります。
3. 正の整数mとnについて、am * anはaをそれ自身にm + n回掛けたものと定義されています。これはam+n*の定義と同じです。
4. 整数が別の整数で割り切れる場合、その整数は別の整数の倍数となります。例えば、8は4で割り切れると言えます。なぜなら、8は4の倍数(2倍)だからです。
5. 有理数は、m/nという形で表すことができます。ここで、mとnは整数であり、nは0ではありません。分母が0であってはならない理由は、0で割ることは数学的に定義されていないためです。
6. 分数a/bとc/dの和は、(ad + bc)/bdで与えられます。例えば、1/2 + 3/4 = (14 + 23)/(2*4) = 10/8 = 5/4です。
7. 有理数a/bの乗算逆数は、(a/b)に掛けたときに1となる数です。乗算逆数はb/aで与えられます。有理数0は乗算逆数を持ちません。
8. 2つの未知数を含む連立一次方程式を解くための2つの方法は、代入法と消去法です。代入法では、一方の変数を他方の変数で表し、もう一方の方程式に代入します。消去法では、一方の変数の係数をもう一方の方程式の対応する係数と等しくなるように操作し、2つの方程式を加算または減算して一方の変数を消去します。
9. 方程式x2 = -1は、実数の範囲では解を持ちません。なぜなら、任意の実数を2乗しても、負の数になることはないからです。
10. 正の数aのn乗根とは、n乗するとaになる正の数のことです。
できなかったこと
有価証券報告書から財務分析
「提供された情報源に財務情報が含まれていない」と言われ、財務分析をしてくれませんでした。おそらく、PDF内の表を上手く読み込めていないようです。 Google AI StudioのGemini 1.5 Proでは可能だったため、NotebookLMで動いているGemini 1.5 Proは、ナーフされているのか、日本語での提供を始めたばかりなのでバグなのか、どちらにしろ読み込めないようです。
複数ソースの分析
試しにトヨタ、日産、本田技研の有価証券報告書を読み込ませ、3社の事業を比較させようとしましたが、「提供された情報源は、トヨタ自動車、本田技研工業、日産自動車の有価証券報告書からの抜粋であり、3社の詳細な事業内容を比較するには情報が不足しています。」と言われ、分析が進みませんでした。これもナーフされているせいかもしれないです。
この記事でご紹介したAI技術の応用方法について、もっと詳しく知りたい方や、実際に自社のビジネスにAIを導入したいとお考えの方、私たちは、企業のAI導入をサポートするAIコンサルティングサービスを提供しています。以下のようなニーズにお応えします。
AIを使った業務効率化の実現
データ分析に基づくビジネス戦略の立案
AI技術の導入から運用までの全面サポート
専門家によるカスタマイズされたAIソリューションの提案
初回相談無料ですので、お気軽にご相談ください。以下のリンクからお問い合わせください。
この記事が気に入ったらサポートをしてみませんか?
