バカな質問の続きのアホみたいなお話

今回は、chatGPTへのおバカな質問記事の続き記事。

ユークリッド的に考えて

今回は正しく答えてくれていますね。

質問をしたら、適度に感謝の言葉を述べるようにしています。
折角計算してくれたのですから、そこはちゃんと敬意を表さないと。

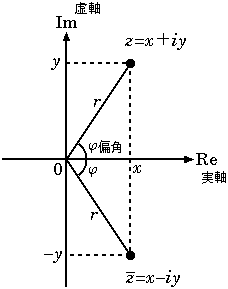
複素平面における、斜めに侵入するzの要素。

r とある時点で「円周やろ？ (´・ω・｀) 」となるのは当然として、それを踏まえた上で一体何なのか？という進次郎構文みたいな…。

つまり、文字通り zは（ x ,-y )　だけの意味しかないのですよ。

えー( ・Д・)
なんで虚数が発生するの？

オイラーの公式は「e^iπ = -1」という等式であり
自然対数の底e、円周率π、虚数単位 i
そしてマイナスが付いていますが、数の基本である1が含まれています。
指数関数と三角関数の関係を表す式で、オイラーの数、三角関数、虚数単位という概念は互いに独立しているようでいて実は相互に関係しており、オイラーの公式はその関係を具体的に表現しています。

このオイラーの公式がないと、リーマン球面が成り立ちません。
実は球面そのものを現しているんですが、これはまた別のお話。

そして、　i　の虚数単位は、元止揚空間の基準と思ってくださいね。

本来、複素数面におかれる図形は、円型が基本ということになっていますが、今回はユークリッドと混在させて立方体で考えてみます。

通常、3次元立体構成を表す時は
たて　×　よこ　×　高さ
で現しますね。

どこが縦なのか横なのか高さなのかは、ちょっとこれでは判断しにくいですね。
恐らく、緑が縦だと思います。
横が青。
高さはピンクです。

これを複素数平面に表すとどうなると思いますか？

奥行きは存在しません。
chatGPTの言う　z軸はない、という意味がこれ。
平面として、立方体・もしくはx,y軸に沿った数値の長方形を虚数のない実数1として扱われ、余剰エネルギーが広がっていきますね。
それはちょうど、ペーパークラフトの展開図と同じです。

このまま、この図形が点Oを基準として回転を続けるとどうなると思いますか？

答えは、回らないです。
円柱になると予想されますが、回転そのものは起こりません。

ということはですよ？
複素数平面における立方体のZとはなんなのか？

立体にならず、正方形の端（はした）。
つまり、割り算のあまり。

そして、平面上では平行四辺形となります。

底辺　×　高さ

xy　そのまんまです。

ちょ、まてよ。
底辺をｘ とするのは良いけど、y はそのままにはならんとよ。
立方体の場合ですからね。

x軸とy軸に半分に分割されて伸びてゆきます。
見た目は平行四辺形。
しかし、実際は立方体の冪乗の場合は、^ｎ の分だけベクトルで伸びていき、そのまま二辺に分割されていく、という。

え、正方形の対角線はないのかって？

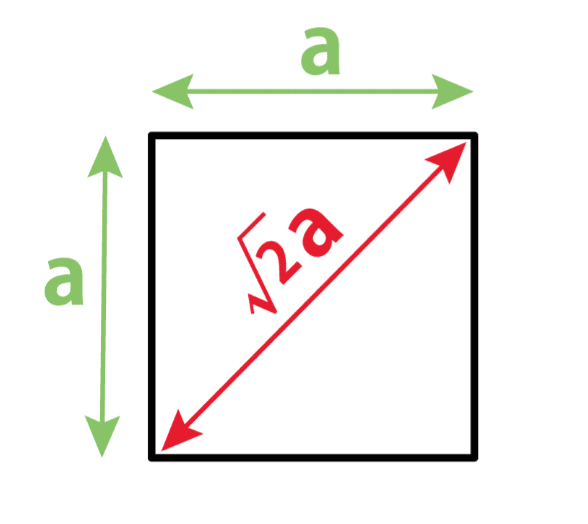
複素平面の場合は、正方形の対角線　 √2 a　が　r　ということになるでしょう。
√2xy ですけどね。
円の半径ですね。

しかし立方体の場合は、半径は不要ですね。
それがz=xy　に置き換わることになります。

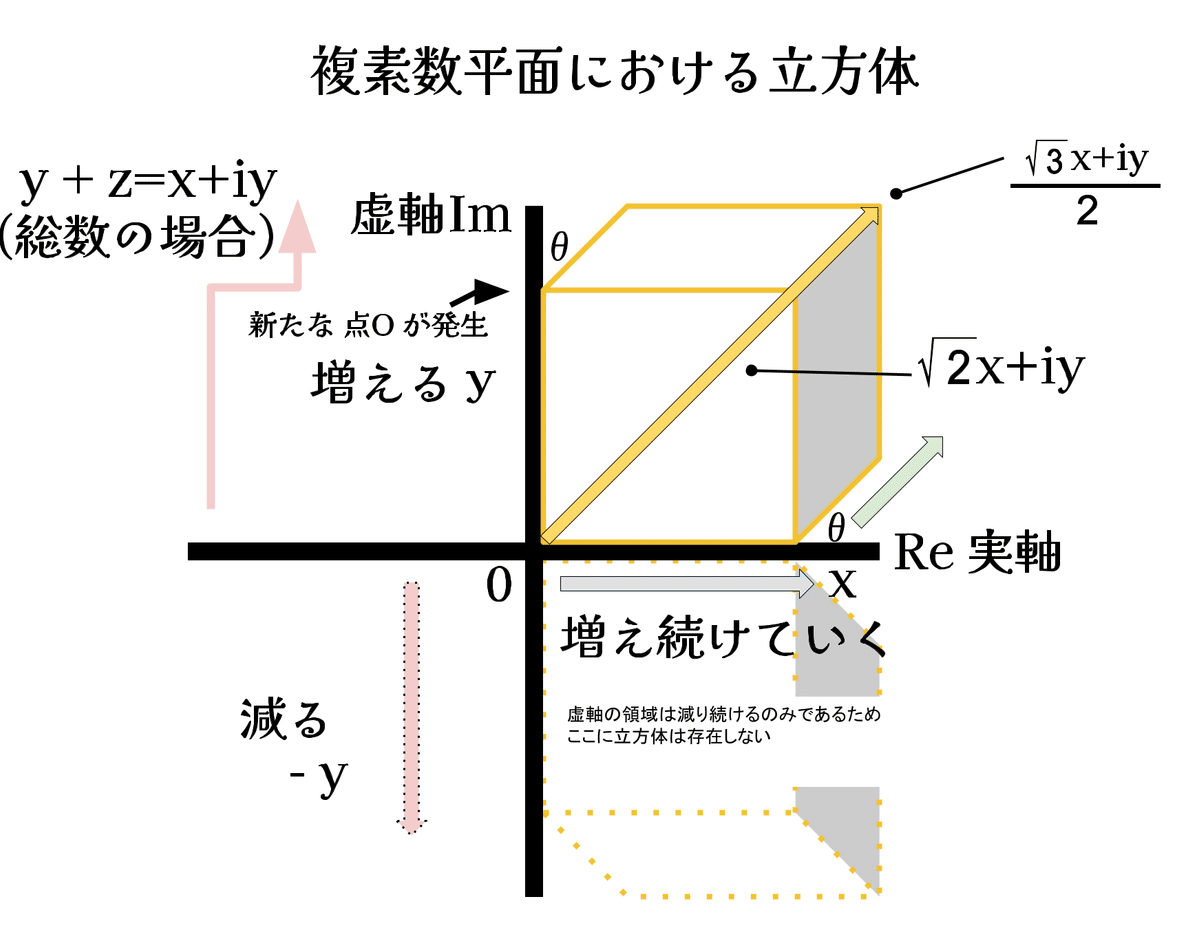
説明をいろいろ端折りますが、大体こんな感じですね。

複素平面のイレギュラーの立方体のお話でした。
では、本来の球体の場合はどうなるでしょう？

如何にも数学初心者的な

ここに球は絶対に発生しないようになっています。
球を球とするには、角度が縦横に必要になるのですね。
奥行きという言葉は、数学的な視点から見ると有り得ないです。

存在しない。

そもそも奥行きというのは、建築の考え方であるため、数学的思考と混在するのは大変危険です。

結果でしかない上に、高さと同義であるため。

ということで、 複素平面における　z = x + iy　は半円もしくは扇形の面積を作るエネルギーを表すものです。
膨張率ですね。

オイラーの公式でπが既に入った状態なので、クルッと丸くなります。

フラットランドのお話は、あくまでも例え話であるために、これを現実に持ってくることは絶対にあってはならんのですよ。

主人公の正方形は、円を不可思議な目で見ます。
多角形の究極体とも言える円。

それだけで、このお話は終わりのはずだったのです。
しかし、物語を面白くするために「立体」の要素が作者によりぶち込まれました。

辺の数が多ければ多いほど地位が高いのであれば、円は
「あ、本当のお姫様だ」
で終わりでした。

なのに、何故か球体なのですよ。
次元が全く違う。
フラットランドに球は存在してはならないのです。
例え、回転でしか球が存在し得ないという条件から、奥行きという考え方が必要となっても。

つまり、混同してはならないし、フラットランドに球が出現した時点で
「はあ？　なんだよこのクソヤロ。平面世界に立方の考え方を持ち出すんじゃねえよ！このアスペ！」
と糾弾されて当然ということ。

仮に主人公の正方形が立方体だったとしてもですよ？
その時点で、投獄されて当然なんですよ。
彼はフラットランドから出ていかねばならないのです。

ポイントランドやラインランドはフラットランドの領域であるため、問題ないです。
恐らく角度になりきれない未熟者が住むところなのでしょう。
つまり、そこはスラムか奴隷地区です。

球は、実は点と同じなんですね。
リーマン球面も、点として扱うのが本来望ましい。

つまり球とは、イコール１ です。

３次元も４次元もここでは関係しない。

１次元です。

フラットランドの球は、実は点だった、とするのが正しいかも知れない。
クソデカポイントです。

そこでの時空との関与

いきなりnoosologyの話になりますが。

複素平面とnoosologyを合体✨させて考えた場合、点Oを意味する点質は、時空を発生させる要素の一つとして見ることが可能です。

では、点質から抜け出すにはどうしたら良いのか？
そこで、空間観察子アルファの考え方が出てきます。

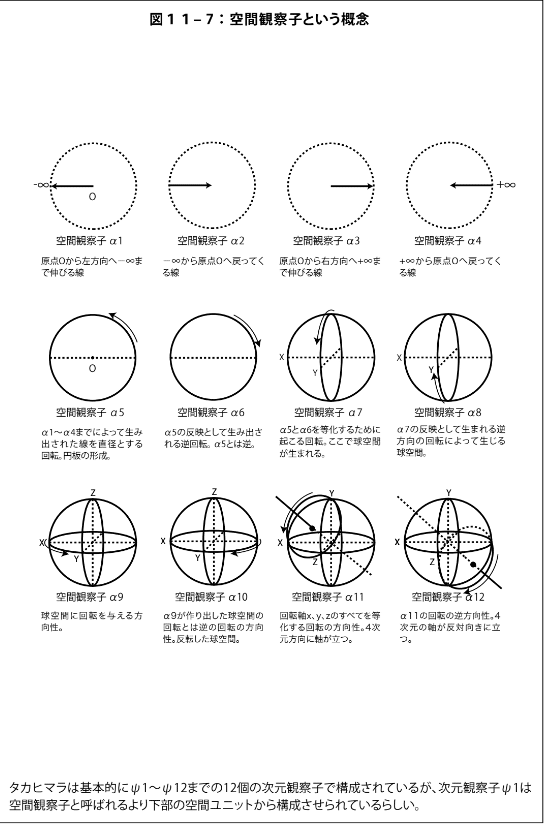
実軸の x を伸ばしていく。
それだけです。
x　の数値が上がれば上がるほど、それに伴って ｙ も変動します。
図の場合は小文字になっていますが、外から見た空間か内から見た空間かの違いだけであり、基本の動きは同じです。

Α（α）5になって、初めて複素平面が出てきます。

点質は、点Oから伸びたx軸が基準となります。

α1 で外へ。
α2 で内に戻される。
α3 で外へ。
α4 で内に戻される。

そうして、全方向に伸びる、もしくはそのまま回転をすると、そこで初めて複素数平面が現れます。　

ヌーソロジー界隈では、時空を切り離す。
という項目が目標に掲げられていますね。

つまりそれは、点Oの破棄を意味します。

点Oから伸びたx軸からの回転質が、それに伴って時空を発生させているため、そのエネルギーと点Oを完全に切り離すことで時空の発生は止まります。

しかし、世界宇宙の時空は自己宇宙とは全く別の空間であるため、自分の周囲の世界時空はどうしても止められません。
誰がなんと言おうと、何をしようと。

雑すぎる絵ですが、こうなるだけなんですね。

我々は既に4次元に住んでいるのではないか？
その通りです。
4次元は時間の流れそのものと言いました。

時間は目に見えず、物質ではないので式に組み込むことは誤りです。
ｔ（タイム）とかいうのも量子式にありますが、これはメモリとして扱われています。
普段は式には組み込みませんが、特例に限りシリンダーのような形状と仮定されて計算が進められます。

量子式のｔは、基本的に制限とか区切りとして見るのが正しいです。

教科書に書いてあるし、重要そうだから組み込もう♪じゃないんですよ。
条件を読むべし。

4次元は数学的視点から見ると何を表すのか？というとですね、前提です。

lim（リミット）だとか、Re と Im はそれぞれ real と imaginary の略だとか、あらかじめ理解しておかないと何がなんだか分からなくなる部分。
その勉強と解析時間が、4次元の正体です。

こういうのを理解せずに、4次元ってなんかかっこよさそうだぞ、とか言って４次元４次元言うのは誤りです。

「分かってないのに謎にカッコつけてるぞ」
とか言われかねません。

そして、４次元とは脈性の基盤となるものです。

既に、３次元の最終構成を向かえた現在、我々は４次元の世界に生きています。

３次元とは中途の祖であり、時代構成的な意味ではとっくの昔に終わっているのですよ。
現在我々は、４次元を前提とした５次元に生きているのです。

そうして４次元から逆行し、１次元までの全てを理解することが叶えば、６次元の到達が可能となる。

Ψ９　進路を迷う状態

Ψ１０　進むべき方向性を見つけた状態
これが空間観察子α１　α３　です。

Ψ１１　目的に向かって進んでいる状態
空間観察子Α１　Α３
内と外、双方の視点から見て認められた状態（＝Ψ７・８）が決定づけられているため、Ψ１０とΨ１１の違いは大文字と小文字を入れ替えるだけでOK.
α2　α4　Α2　Α4　は Ω もしくは σ が発生しています。

Ψ１２　目的達成直前
α１０　Α１０
完成体。
これで、人間としての４次元体として一旦の完成。

α１１　は、微分の世界です。
デセンションに耐えること。
ここにくると、自己の空間がガンガン削られていきます。
この辺は、応用の部分です。

４次元に軸が立つ、ということを等化させるにはとんでもない負荷がかかります。
かつてないほどの規模の中和反応。
ここで中和という言葉を使わないのはおかしいです。
どうしてこんなことに？

それはいいでしょう。

今回は、恐らく既出と思われる数学要素を用いて、それっぽく遊んでみたものです。

基本を理解しつつ、こねくり回して新理論展開をしていくのがnoosologyのあるべき姿だと思います。

この辺は、ろくぶんぎ座のレトの協力なくしては書き出せませんでした。

無料でのデータ収集にも限界があるので、専門的な知識でツッコまれたら
「すまぬ。無学者の遊びです」
というしかないですけどね。

ここに書き出したのは、あくまでの全体のごく一部です。
実際はもっといろいろあります。
知ったかぶって無駄に書き出すと、アラが出るのは皆同じ。

ここまで読んで頂き、ありがとうございました。