数学史から見る「掛け算の順序問題」
「掛け算の順序問題」というのがある。Wikipedia には、「掛け算によって解が得られる算数の文章問題について、特定の順序で書かれた式のみ正解とする採点方針と、どの順序で書かれた式でも正解にすべきであるという主張の対立である」と書かれている(https://ja.wikipedia.org/wiki/かけ算の順序問題)。東洋経済オンラインでも2021年7月に、「「掛け算の順序問題」はやっぱり決着がつかない」と記事が上がっている(https://toyokeizai.net/articles/-/442140)。
私が最初にこの話題に触れたのは 5ちゃんねる(2ちゃんねる)のまとめ記事だったと思う。小学2年生の算数のテストで
「8人にペンをあげます。1人に6本ずつあげるには、ぜんぶで何本いるでしょ うか。」
という問いに対し、子供の解答が
しき:8x6=48
答え:48本
となっていたが、両方とも✔︎で、下に正解が赤ペンで下のように書かれていた。
6x8=48
48本
まとめサイトの反応には、6x8=8x6だから採点する方が間違っているというコメントばかりだったと記憶している。また、その頃教えていたクラスでこの事例を紹介したところ、学生は皆6x8=8x6だから✔︎にするのはおかしいという意見であった。
1. 掛け算の順序は、子供たちが問題文を理解したかどうかのアピール
しかし、私なら、教師が授業で掛け算の式にするとき最初にひとつ分の量を書いて、次にそれがいくつあるのかという個数をかく、テストの時もその順番で式を書く、と指導していたという前提のもとで、式は✔︎、答えを○にする。
なぜ式に✔︎をするのかというと指示通りに答えていないからである。問題文ににはそのような指示はないと反論する方もいるだろうが、授業の時にそのように指導しているのであらば問題ない。指示通りにことを進めるというのは数学に限らず、日常生活でも大切である。指示を無視して、自分流のやり方でしたら事故にあったという話はよく聞く。上の問題では、指示されたやり方と違った方法で問題を解いたらたまたま答えが一緒だった、ということにすぎない。
教師がなぜ解法についての指示を出すかというと、子どもたちが、掛け算の文章題で、一つ分の数と個数を区別できていることを確認したいからである。先の問題はおそらく掛け算の単元の学習がおわった時点でのものである。多くの子供は、問題に出てくる数字を二つ掛ければ正解が得られることがわかっている。したがって、一つ分の数がいくつで、それが何個あるのかを気にせずに、問題に出てくる数をその順番でかけて式を立てる可能性が高い。そこで、授業で指導した通りの順番、ひとつ分の数が先、個数が後という形で式を書いてもらうのである。子どもたちの側からすれば、式を指定された順序で書くことで、自分は問題がわかっていますよ、と教師に証明しているのである。一方、教師は、6x8と回答した子供は、授業での指示を無視したか、授業での指示を忘れたか、あるいは、授業を理解できていなかったか、のいずれかである、と解釈する。
上のような説明をしたあと、学生に対して改めて「指定した解法とは異なったやり方で正解を得られた場合に○にするのか」という質問をしたら、今度は、答えは○にするけれども、式は✔︎にするという意見に変わった。中には、指示通りにしなかったのだから、式だけでなく答えも間違いにして良いという者もいた。彼らは、例えば二次方程式を因数分解を使って解け、という問題に対して、解の公式を使ったら答えがあっていても✔︎にされたことがあるからだ、という。
アメリカのとある大学で教えていた時は、解答方法を指定する問題においては、指定された解法とは違うやり方で正しい答えが得られた場合に、式には点数を与えず、答えに部分点を与えるという採点基準であったが、別のところでは式が間違っていたら答えがあっていても点数を与えないという採点基準になっていた。その解答方法と採点基準は注意事項として試験前に学生たちに伝えることになっている。問題文には書かれていないことも少なくない。式だけ✔︎にするか。両方とも✔︎にするのかというのは人それぞれであろう。しかし、指示通りの解法でとかなければ、式を✔︎にするという点は同じである。
2. 掛け算の順序問題の本質
新型コロナで無職になった時に、「掛け算の順序問題」を思い出して検索してみると、主張は2011年頃に集中している。その中で最初に目に留まったのが白川克氏のブログである。
https://blogs.itmedia.co.jp/magic/2011/12/6886-2d5b.html
私が見たまとめサイトで見た写真は白川克氏のブログに記載されていたもののようである。彼が疑問に感じたことを4つほど紹介しておられる。大まかに言えば、彼は掛け算の式を書くときに、その順序にルールがあるのはわかるが、掛け算は交換法則が成り立つから、そんな順序のこだわるはおかしい、と主張しているように思う。
白川氏以外にも多くの方がこの問題について書かれている。今ではリンクが消えてしまったものも多く、全てに目を通せたわけではないが、白川克氏の他に高橋誠氏、わさっき氏(本名がわからないのでこのブログネームで呼ばせていたただきます)、黒木玄氏、開米瑞浩氏、菊池誠氏のブログを読むことができた。いずれも、6x8を✔︎にするのはおかしいという立場である。彼らを順序反対派と呼ぶことにしよう。
6x8を✔︎にするのを正しいとする者、順序賛成派と呼ぶことにする、では、伊藤宏氏の調査(http://mnavidata.edu-c.pref.miyagi.jp/manage/wp-content/uploads/tmpFile/practice_research/01B0010.pdf)が印象に残った。彼は、日常生活の中で計算が活用できる子供の育成を目指した学習指導の一試み、で、小学校3年生の子供達を対象に計算の意識などを調査した。その第5問として、次のような問いがあった。
「ここに4まいのふくろがあります。かずや君が,1まいのふくろにりんごを3こずつ入れました。 りんごは,ぜんぶでなんこありますか。
① 答えを出すための式を書いてください
② どうして、そのような式になったか、絵に描いて教えてください」
この問は単元末のテストではないので、15%ほどの子供たちが、掛け算の問題と認識できなかったようである。それはさておき、①に対する解答として、8人が3 x 4、21人が4 x 3 と書いた。そして、この29人全員が②では正しく絵を描くことができた。彼は、
文章の意味はわかるのだが、乗法の意味が明確に理解できていないということを示している。誤答を見ると,乗法を使うことを見通すことはできても,文章に書かれた数字を順番に並べて,「4×3」という回答をした児童が 多かったのは,そのためである
と結論している。乗法の意味を理解していないというよりは、これは掛け算の問題だから、出てくる二つの数をかけておけばいい、と子供たちは考えていたのではないかという気がするが。試しに、①と②を逆に出題した時の子供たちの①の解答がどうなったのか、興味がある。しかし、伊藤氏はなぜ掛け算の式がひとつ分の数が先で、その数が後というふうに書くことが「正しい」のかという説明はなかった。
順序反対派のブログや書物の中に、順序賛成派の言葉がいくつか紹介されている。順序賛成派の主張が正しく紹介されているとすれば、順序賛成派はこういうルールになっているからと繰り返すばかりで、何故そのようなルールで書くようになったのかはわかっていない印象を受ける。だから、順序反対派は、順序賛成派のこだわりに疑問に感じるのであろう。
掛け算の順序問題の最も古い記録は1972年の朝氏新聞記事らしい。高橋氏がブログで紹介していた(https://ameblo.jp/metameta7/entry-10196970407.html)。私からは、記事に出てくるKさんは、式なんかどうでもよい、答えがあっていたんだから○にしろと主張しているように見える。Kさんの展開する計算方法は大変面白いが、これはKさん自身のアイデアで、Kさんの子供がこの考えで式を立てたわけではないと思われる。もし、子供がこのように考えていたとしたら、授業を全然聞いない証拠でもある。教育委員会などからの返事も、ルール設定の意図を、教員に確かめることなく、こう言っておけば良いだろうという、投げやりなものに思える。
こういう言い方をするとなんだが、順序反対派の主張は、答えがあっていれば、解答方法の指示なんか無視しても良い、と聞こえる。しかし、指示を無視しても良いと主張すると語弊があるので、話の矛先を交換法則の成り立つ掛け算に順序があるのはおかしい、とすり替えていると感じる。正直なところ、白川氏も、娘さんがテストで✔︎をもらったから、先のブログを書かれたわけで、○だったら、掛け算の順序のことなど、話題にすら上げなかったのではないか、と思う。
それに対して、順序賛成派も掛け算の順序を子供たちが問題を理解しているかの確認に使ってはいるが、なぜ順序があるのかという明確な答えが見出せないでいるように見える。だから、Kさんのような計算方法を出された時に答えが詰まってしまう。
3. 交換法則は常識か
数学に限らず、指示通りにするというのは重要なことである。指示を無視してあるいは忘れて大ごとになった経験のある方も少なくないだろう。しかし、指示には整合性が伴わないといけない。不適切な指示は、逆に、従えば大ごとになる。したがって、「掛け算の順序問題」は掛け算の式を特定の順序で書くという指導に整合性はあるのかということである。
順序反対派はこの指導を整合性がないと主張する。その根拠は、掛け算では交換法則が成り立つからである。彼らは、交換法則は世間の常識である、という。しかし、それは数学の常識ではない。現代の数学では、掛け算はふたつの同じタイプの数学的対象に対して行われる操作で、(1)結果がただ一つに決まり、(2)閉じており、(3)結合法則を満たし、(4)単位対象が存在するという4つの条件を満たすものと定義されている。閉じているというのは、操作の結果がまた同じ数学的対象になることで、例えば、数と数と掛け算の結果は再び数に、行列と行列の掛け算の結果は再び行列になる、ということである。結合法則は、3個以上の対象があったとき、どの2個から操作を始めても結果は同じになるということである。単位対象は、ある対象に単位対象との操作をすると結果が元の対象になる、すなわち、何もしなかったのと同じ結果になることである。例えば、どの数に1をかけても結果はは変わらない。従って、数の単位対象は1である。
数学的対象は数だけでななく図形や集合など色々ある。掛け算は各対象の上に独立に定義される。したがって、対象や掛け算の定義の仕方によっては、交換法則の成り立たないケースも出てくる。周知の通り、数の上では掛け算の交換法則は成り立つ。しかし、例えば、行列では掛け算の交換法則は成り立たない。数学者である黒木氏は交換法則の成り立たない掛け算の例を取り上げていたが、他の方は、全く取り上げられていなかった。しかし、黒木氏も、交換法則の成り立たない掛け算を学ぶときに注意すれば良いと言われているので、基本的には交換法則は当たり前に成り立つと考えておられるようである。
21世紀になって急激に流行し始めたデータ解析に行列は必要不可欠である。しかし、その行列では交換法則が成り立たない。2000年以降、アメリカの大学では、MATLAB などの行列の扱うことのできるソフトウェアを授業で使っている。日本でも同じようなものではないだろうか。したがって、2011年当時で、すでに世間でも掛け算の交換法則は常識ではなかったのではないだろうか。
4. 交換法則の証明は、交換法則が直感的に正しくないことを意味している
わさっき氏は交換法則の証明を数種類紹介し、掛け算の交換法則は正しいと主張した。彼が引用した証明は全て、ペアノの整数の公理に基づく、数学的帰納法による証明である。したがって、数の上で成り立つ性質であるということしか証明していない。
ここで、クイズを一つ。
世界で最初に数の掛け算の交換法則を証明したの誰か。
答えは、ジュセッペペアノではなく、古代ギリシャの数学者ユークリッドである。ユークリッドは紀元前3世紀に「原論」を編纂したことで有名である。「原論」とは全13巻からなる数学書で、古代ギリシャの数学の結果を、論理的に再構成したものであり、数学を今のような公理と定義から命題を論理的に証明する形にした元祖である。第1巻から4巻までの幾何学が特に有名で、ユークリッド幾何学と呼ばれる。幾何学だけでなく、素数や完全数など数(整数)の性質についてもまとめられている。「原論」は古代ギリシャ数学の再構成なので、ユークリッドが証明していない命題も多数含まれている。もしかしたら掛け算の交換法則はユークリッド以前に証明されていた可能性もあるが、ここでは便宜上ユークリッドが証明したことにしておく。
掛け算の交換法則とその証明は「原論」の第7巻で述べられる:
命題VII.16 もし二つの数が掛けていくつかの数ができたなら、それらの造られた数たちは等しい。
Proposition VII.16. If two numbers multiplying one another make some (numbers) then the (numbers) generated from them will be equal to one another.
英文は、Richard Fitzpatrick, Euclid’s Elements of Geometry からの引用である。日本語訳は私自身がした。「いくつかの数」はフィッツパトリックの「some (numbers)」の直訳であるが、命題の証明を読むと、二つの数A、Bをかけるとき、二つの数 AxB と BxA が作られることがわかる。この命題はそれらが等しいということを述べている。
証明は長いのでここでは割愛する。証明に興味のある方は、北秀和氏のホームページに詳細なものがあるので、参照していただきたい(https://euc-elements.matrix.jp/indexframe.html)。
もし AxB とBxA とが同じ数であることが自明なら、ユークリッドはわざわざ交換法則の証明はしなかったであろう。掛け算の交換法則を命題にして、それを証明したということは、ユークリッドは AxB と BxA とが同じ数なのではないかという疑問を持っていたことに他ならない。
5. 掛け算の定義からみる交換法則
交換法則の証明を紹介した高橋氏は掛け算の定義も紹介している(https://ameblo.jp/metameta7/entry-12645817441.html)。すべてペアノの公理系に基づく帰納的定義である。一方、ユークリッドは「原論」のなかで掛け算を次のように定義している。
定義 VII.15 数に数を掛けるということは掛けられる数が前者の数に含まれる単位の数と同じ数だけ足されることである。
Definition VII.15. A number is said to multiply a(nother) number when the (number being) multiplied is added (to itself) as many times as there are units in the former (number), and (thereby) some (other number) is produced,
ユークリッドは数をその数に含まれる単位の数で表している。この単位は1のことで、例えば、3は単位の数、つまり、1を3個含んでいるという具合である。この定義では、数Aに数Bをかけるということは、BをA回たすことである。すなわち、
$$
A \times B = \underbrace{B+B+\cdots+B}_{A}
$$
となる。また、掛けられる数は後者の数Bで、前者の数Aは掛ける数であると書かれている。したがって、Bがひとつ分の数、Aがその個数になる。これは、日本風の流儀とは逆で、Wikipedia で記されているようにアメリカ流である。高橋氏の紹介された定義の中では、高木貞治のものが、この形になる。
次に、ユークリッドは「積」の定義をしている
定義 VII.16. 二つの数が掛け合わされたとき、その結果を平面という。その平面の辺はそれぞれ掛け合わされた数である。
Definition VII.16. And when two numbers multiplying one another make some (other number) then the (number so) created is called plane, and its sides (are) the numbers which multiply one another.
ここでいう「平面」が積のことである。この語は、フィッツパトリックの英訳では単に「plane」、ハイベルクのギリシャ語訳は ἐπίπεδος (epipedon)となっている。したがって、定義 VII.16 は、2つの数A、Bの積は、2つの辺の長さがA、Bの長方形の面積であると、図形を意識していることがわかる。定義 VII.17~19では、立体数、平方数、立方数を同じように定義している。
ユークリッドは、積において、二つの数のうちどちらが掛ける数で、どちらが掛けられる後かについては言及していない。それゆえ、Aが掛ける数でBが掛けられる数の場合と、それを逆にした場合の2つの積が考えられる。Aが掛ける数でBが掛けられる数の場合はBをA回たすので
$$
A \times B = \underbrace{B+B+\cdots+B}_{A}
$$
になる。一方、掛ける数とかけられる数を交換すると、AをB回足すことになるので、
$$
B \times A = \underbrace{A+A+\cdots+A}_{B}
$$
になる。つまり、掛け算の交換法則、AxB = BxA、は
$$
\underbrace{B+B+\cdots+B}_{A} = \underbrace{A+A+\cdots+A}_{B}
$$
ということになる。ユークリッドはどう考えたか正確なところはわからぬが、AとBが違う数であれば、数自体も足される個数も両辺で異なる。こうなると一見で、両者が同じであるというには無理がある。それゆえ、ユークリッドは、掛け算の交換法則を公理ではなく、命題にして、証明したと考えられる。
6. 縦 x 横 = 横 x 縦 が成り立たないパラドックス
ユークリッドは数を単位線分の整数倍の線分で、積を「平面」で表しているので、掛け算をアリー表示で考えていると思われる。しかし、どちらが縦でどちらが横かは定義していない。実際、「原論」では数を表す線は縦向きであったり、横向きであったり一定しない。例えば、3x5は定義から5+5+5なので、5個のものを3つ分並べるのだが、「原論」7巻には「平面」を表す図形は出てこなので、縦に並べるのか、横に並べるのかはっきりしない。つまり、3x5は1行5個のものが3行ある
●●●●●
●●●●●
●●●●●
なのか、1列5個のものが3列ある
●●●
●●●
●●●
●●●
●●●
なのかは、はっきりしない。
どのように並べても結果は同じだから、ユークリッドは特に定義しなかったのかもしれない。しかし、もしかしたら、古代ギリシャ以前では、並べ方によって、数が異なるという認識があったのだろうか、と考えたら、不意に、古代ギリシャの歴史家ヘロドトスの次の有名な言葉が思い起こされた。
「王は各自に平等な正方形の班地をあてがって(中略)、毎年年貢を納める義務を課してそれを収入の財源にしたという。 もし河が何人かの班地の一部を持ち去るようなことがあれば、 (中略)王はその土地がいかほど減少したかを測量させたものである。私はそれが幾何学の案出された淵源であり、それがギリシアへ渡来したものと考える」
上の訳は山岡緑氏の「平面図形の幾何学と歴史」からの引用である。
王はなぜ「正方形」の土地を与えたのか。「長方形」ではいけなかったのか。
ところで、この箇所は、「正方形」ではなく「方形」と訳されることの方が多いと思う。上垣渉氏の「初めて読む数学の歴史」でも「方形」と書かれている。辞書で調べると「方形」は四角形、特に正方形とある。しかし、J.D.Godley が翻訳編集した英語版(http://data.perseus.org/citations/urn:cts:greekLit:tlg0016.tlg001.perseus-eng1:2.109.1)ではこの部分は an equal parcel of land となっている。parcel とは四方を道路で囲まれた街の「1区画」を意味する英語である。英語圏で「1区画」といえば、正方形が普通である。さらに対応するギリシャ語では τετράγωνον (tetrágo̱nos)となっており、これは正方形という意味で、ユークリッドは τετράγωνον を「平方数」という意味でも使っている。従って、山岡氏の訳の通り、王は確かに「正方形」の土地を与えたのだ。
王が全ての国民に土地を与えたのは、税収のためであった。全てが同じ広さということは、皆納める年貢の量は同じと考えられる。繰り返すが、なぜ、「正方形」の土地を与えたのか。「長方形」ではいけなかったのか。ヘロドトスも書いているように当時のエジプトでは、測量術が発達していた、形が違っても同じ面積の土地を提供することは容易であったと思われる。ここから、王は面積ではなくその形、正方形であること、にこだわったと考えられる。
ここでもう一つのクイズを出そうと思う
下のような5m x 2m の畑に麦を植える。畝と畝との間が40cmで、畝と畦は20cm以上開ける、一つの畝では苗を30cm間隔、苗と畦とは15cm以上開けるとすると、この畑には何本の苗を植えられるか。

この問題はいわゆる植木算の問題である。
まず一番上の畝に苗を植えていく。
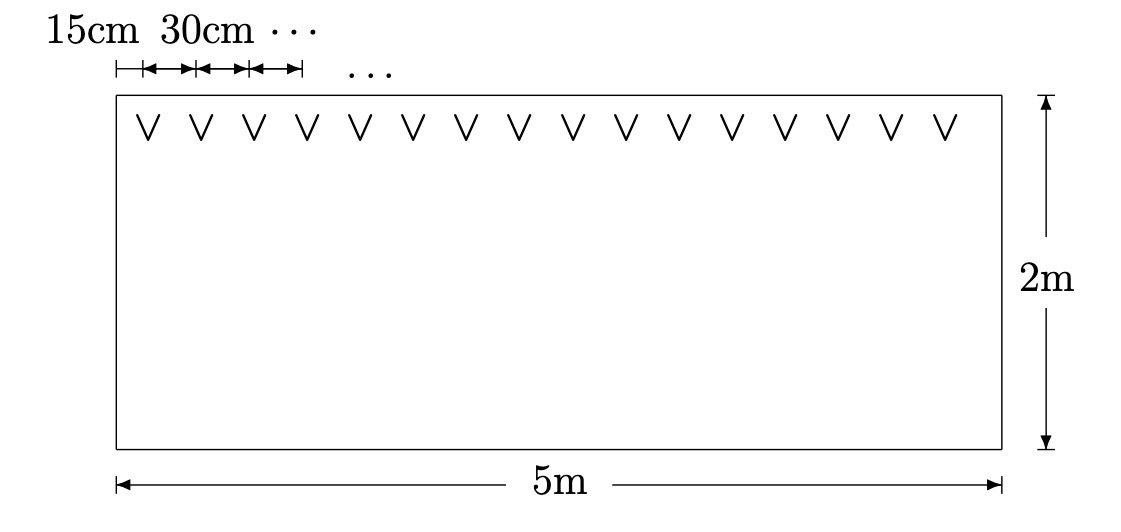
最初と最後の苗は端から15cm づつ離すので、苗を植えられる範囲は 5m−15cm x 2=460cm 分になる。苗と苗との間隔は30cm なので、一つの畝に植えることのできる苗の数は
$$
460 \text{cm} \div 30\text{cm} = 15 \text{ あまり}10
$$
となって、15本となる。苗は範囲の両端にも植えられるので、1本足して、16本の苗を植えることができる。
次に畝が何列できるかを同じやり方で計算する。
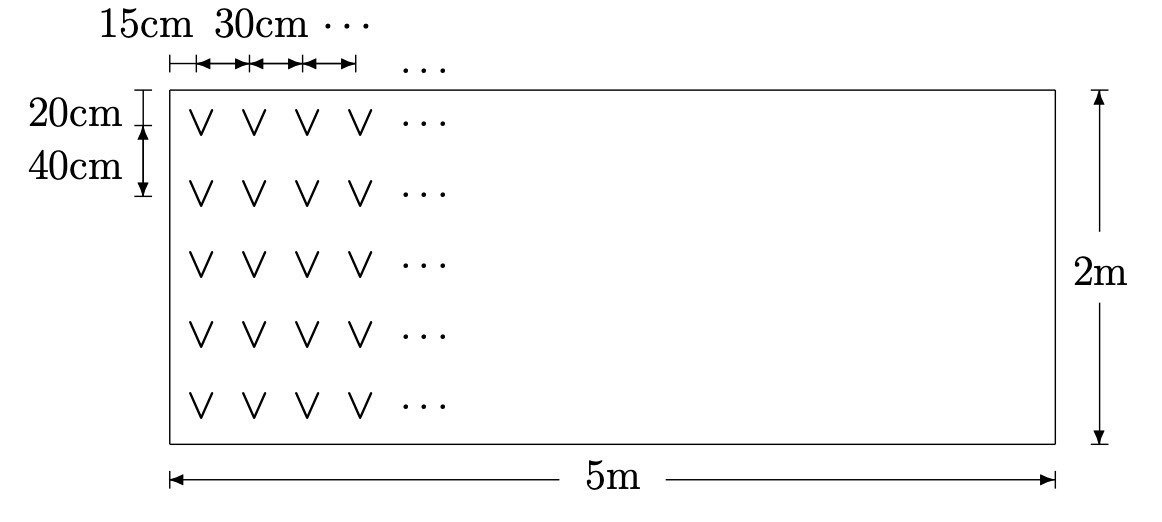
最初と最後の畝は端から 20cm づつ離すので、畝を作れる範囲は2mー40cm =160cmになる。畝同士の間隔は40cm なので、畝の列数は
$$
160 \text{cm} \div 40\text{cm} = 4
$$
となって、4列であるが、両端にも畝は作れるので、1列足して、5列できることになる。
したがって、この畑に植えることのできる、苗の本数は
$$
16 \times 5 = 80
$$
となり、80本の苗を植えろことができる。
この問題には正解が他にもいくつかある。上の解答では畝を横向きに作ったが、縦向きでも構わない。

縦に畝を作ったとき時に、一つの畝に植えられる苗の本数は
$$
\lceil (2\text{m}-30\text{cm}) \div 30\text{cm} \rceil +1 = 6
$$
となる。 $${ \lceil x \rceil }$$ は $${ x }$$ を超えない最大の整数という意味である。この畑にできる畝の列数も同様に、
$$
\lceil (5\text{m}-40\text{cm}) \div 40\text{cm} \rceil +1 = 12
$$
と計算できる。したがって、この畑に植えることのできる苗は
$$
6 \times 12 = 72
$$
となって、今度は72本しか植えられない。畝を横向きに設置するよりも1割減ってしまった。
こういう人は滅多にいないと思うが、斜め、同心円状、放射状に畝を設置するとまた違った数になる。従ってこの問題の解答は無数にある。
この問題の面白いところは、面積が同じなのだから、縦向きに植えようと横向きに植えようと、同じ数の苗を植えられると思っていたが、向きが違ったら、植えられる苗の数が同じではなかった、つまり、縦 x 横 = 横 x 縦が成り立たないというパラドックスになる。この形の畑では、植えることのできる苗の数は1割の差が出てくる。当然収穫にも差が出る。しかし、当時の年貢は収穫ではなく畑の広さで決まっていたので、どちら向きに植えても年貢は同じである。しかし、うっかり縦向きに植えてしまったなら、自分の手元に残る量が少なくなる。
ここから先は私の推測であるが、当時の壁画から、エジプトでは麦を一直線状に植えていた様子が窺える。畑にその直線、畝、が何列か並んでいただろう。時のエジプト王は長方形の畑だと、畝の向きにによって収穫が大きく変わるので、税に関する不公平が出ると考えたのではないか。すでに文句が出ていたかもしれない。王は畑が洪水などで一部でも欠けると、すぐに測量士たちを派遣して、欠けた部分の面積を求め、そこから税を再計算したくらいなので、畝の向きによる収穫の違いについても敏感であったと思われる。正方形ならば、横向きでも、縦向きでも、同じ数だけ畝を作ることができ、ひとつの畝に植える苗の数も同じになるので、収量も同じになり、不公平がなくなると考えたのではないだろうか。
上の問題では、苗を植えられない部分、つまり、割り算で余りがでてくる。畝を縦向きに設置するのと横向きの設置するのとでは、余りの大きさが異なるので、植えることのできる苗の量が異なってくる。それゆえ、交換法則が成り立たないのである。逆にいえば余りをなくせば、交換法則は成立する。割愛しておきながらなんではあるが、ユークリッドは命題VII.16 の証明に、割り算の割り切れるという性質を使っている。掛け算の交換法則の証明に割り算とはと驚くかもしれない。重要な点は、割り切れて余りがでてこない、という点である。
7. 反復説
数学史を数学教育にという動きがある。古いものは明治期の数学者、高木貞治の数学史わさび説がある。計算機のなかった昔の人たちがどのよう工夫して計算をしていたのかという子供達に体験してもらうことで、理解を深める狙いもある。数学史を使った研究授業も多く実施され、概ね結果は良好である。
最近は、H.U.ジャンクビスト氏が、子供が学習していくことは人類が学習していくのと同じことを繰り返す、という反復説という考えに基づいて、数学史を使って教育する考え方(Jankvist, A categorization of the whys and hows of using history in mathematics education, July 2009, https://www.researchgate.net/publication/226049853_A_categorization_of_the_whys_and_hows_of_using_history_in_mathematics_education)を提唱している。
人類は最初、縦 x 横 = 横 x 縦、つまり、掛け算の交換法則は成り立たないと考えていた可能性がある。しかし、ユークリッドは、掛け算の交換法則が成り立つことを証明した。反復説を当てはめると、子供たちは最初、掛け算は順序を変えると違うものになるという認識を持つのではないだろうか。九九を覚えたり、問題を解くうちに、だんだんと交換法則が成り立つことに気づいていくというのが自然な理解の仕方なのではないだろうか。
掛け算といえば、長方形を思い浮かべる人も多いと思う。ユークリッドも長方形の面積を積と定義している。ところが、縦長に置くいた長方形と横長においた長方形はその用途が違う。例えば、印刷をするとき、紙の向きは重要である。縦向きに置いたのと横向きに置いたのでは、橋が切れたり、必要以上に間伸びしたり、違った印刷物が出来上がる。個人的な話で恐縮だが、子供の頃、よくウルトラ怪獣の絵を描くのが好きだった。キングザウルス3世のような4つ足の怪獣は画用紙を横長に使って、ウルトラマンなどの2本足で立つものは縦長使ってに描いていたことを思い出す。まだ、足し算を習う前のことであったが、子供心に、縦と横を交換すると、用途が異なるというのがわかっていたのだと思う。こういう経験があると、掛け算は長方形の面積と言われた時に、交換法則が成り立つと言われてもピントこないこともあるのではないか。
試しに、掛け算を学び始めたばかりの子供たちに、3x5をアリー表示にした
●●●●●
●●●●●
●●●●●
と
●●●
●●●
●●●
●●●
●●●
において、● の数が同じかどうか、数を数えないで比べなさい、という問を出したときに、どのような答えるのか興味がある。
白川氏はどちらも同じだというが、点の数が同じなだけであって、配置が明らかに異なる。計算を学び始めた子供たちが配置が違うから、点の数も違うと答えても不思議はない。たとえば、行列では前者型を3 x 5行列、後者の型を5 x 3行列と呼び、たとえ、その要素が全て同じ数であったとしても両者は=では結べない、全くの別物である。
高橋氏は中国では掛け算をアリー表示で教え、乗数非乗数の区別をしないので、教えるのに苦労していると書いてあった。教科書のコピーが出ていたが、右に3x5、左に5x3、と書かれている。それらが、同じと言われても面食らうだけなのではないだろうか。
8. ルールに従って書けば、他人にわかってもらえやすい。
反復法の考え方をさらに進展させると、子供たちの数学学習において、文字の導入のところで一悶着があるはずである。実際に文字式でつまづく子供は少なくない。つまづいた子供たちには、問題文をよく読んで、式をきちんと書くように指導するようにしている。「きちんと」書くというのは、数式を書くときのルールを覚え、それに従って書くこと、という意味である。文字式計算は数値計算と変わりはないので、一度式を立ててしまえば、後はそれほど難しくはない。文字式は中学校1年生で学習する単元だが、この文字式を書くときのルールが、指定された順序で掛け算の式を書くことと関係がある。
問題を解くときに式を立てることは、その問題の内容を数学の言語に翻訳していることになる。数学の言語というからには、それに使われる記号や記号を意味ある形で組み合わせていくルールというものが存在する。文字式を学ぶときに最初に言われることは、文字と数字を含む式(単項式)は数字を先に文字を後に書く、文字はアルファベット順をに書く、というルールを習う。例えば、
1つ分量が $${x}$$ のものが6個あるときに、全部でどのくらいの量がありますか
という問いに対して、誰もが
$$
6x
$$
と答えるであろう。
$$
x6
$$
と書くものはまずいない。交換法則という点からすれば、いずれの書き方でも構わないはずだが、$${6x}$$ のみを正解とすることが多い。優しい先生なら部分点はくれるかもしれないが、$${ x6}$$ はほぼ確実に✔︎である。理由は簡単で、そういうルールで書くようになっているからである。日本だけでなく世界のどの国でも、このように書くよう指導される。
自分で書いて自分で見る分には、どんなルールで書いても構わないだろうが、答案など他人に見せる場合は、その他人も自分も理解する共通のルールに従って書かないと、相手はわからない。数値だけの式でも同じである。従って、掛け算の式を書くときに、ひとつ分の数が先、個数が後、というように指定することは正しい。従って、交換法則が常識だからということは、式の書き方に順序があるということを否定する理由にはならない。それとも、順序反対派は交換法則があるのだから、x6 を✔︎にするのは間違っている、という主張して、教育委員会に手紙を書いたりするのだろうか。
この話は文字式の話であって、掛け算の話ではないというものもいると思うが、文字を使おうと使うまいと、掛け算の話である。文字を使ったときに掛け算のルールが変わるというのは笑止千万である。文字式で成り立つことは、掛け算記号の省略以外、全て、数字だけの式でも成り立つからである。
9. ひとつ分の数が先か、個数が先か
次に問題になるのは、ひとつ分の数を先に書くというルールである。このルールができた理由を説明した人は見つけられなかった。順序反対派でなくとも、なぜ、ひとつ分の数が後ではいけないのか、という疑問が湧くのは普通だろう。
掛け算の書き方に順序ができたのは、掛け算記号ができたからである。掛け算記号 $${\times}$$ は1631年にイギリスの数学者オートレッドが本格的に用いたと考えられている。等号 $${=}$$ は1557年イギリスの数学者レコードによって使われたのが最初であるであると考えられている。従って、「6に8を掛けた結果は48に等しい」を
$$
6 \times 8 = 48
$$
と記号で書くようになったのは17世紀以降のことである。数学の歴史は3000年以上あるが、数式の歴史は300年ほどでしかない。それ以前はどうしていたかというと、そのまま文章で書いていた。式に直すという行為はないので、順序云々という主張の対立は生まれなかったと思われる。掛け算記号ができた当時は、問題文等に書かれた順番で掛け算の式を書いていたと考えられる。
10. 世間の常識を打ち破ったら、掛け算の書き方の順序ができた
19世紀のスコットランドの数学者ジョージ ピーコックは1830年に出版した「代数学」(A Treatise of Algebra、1842年に改訂版の1巻、1845年に同2巻を刊行)の中で、代数学を論理的にに取り扱うために、算術的代数(Arithmetical Algebra)と記号的代数(Symboliccal Algebra)とに分類した。
当時の常識では、数は自然数および自然数の比で表せる有理数だけであった。教科書なども、自然数と有理数をのみを扱うことを前提でに書かれていた。たとえば、計算の途中で負の数が出て来れば、そこで計算をやめて、この解答は無意味なものであると結論していた。しかし、ピーコックは、負の数や無理数も取り扱うことのできる代数学を構築しようとしたのである。
ピーコックは算術的代数での対象は自然数に、足し算引き算掛け算割り算など演算は通常の意味のものとした。取り扱うことのできる数は自然数に限定されたので、たとえば、引き算では小さい数から大きな数は引けないなど。演算にはいくつか条件がついた。
一方、記号的代数では対象はなんでも良くなり、演算は、結果の意味を考えず、計算自体が意味あることと考えた。つまり、引き算で小さな数から大きな数を引く時でも、そこで止まらずに、最後まで計算するようにした。これは、式の計算をあらゆる解釈から独立した記号を変換する操作として捉えている。
さらに面白いことに、彼は算術的代数で成り立つ性質は、記号的代数でも成り立つと考えた。例えば、冪の法則
$$
a^m a^n = a^{m+n}
$$
は自然数の上では成り立つし、証明も可能である。ピーコックは、この等式は算術的代数で成り立つのであるから、$${m}$$、$${n}$$ がどんなものであっても成り立つ、と考えた。普通は、$${m}$$ が負の数や有理数の時の、$${a^m}$$ の定義を考えてから、上の法則が成り立つかどうか考えるのだが、この場合は逆に、上の法則が成り立つように $${a^m}$$ を定義したと言える。
また、等号「=」についても、算術的代数では計算した結果が同じであるという意味であるが、記号的代数では、代数的結果、つまり式をルールに基づいて変形して得られたもの、という考えである。この意味において、交換法則は算術的代数では成り立つが、記号的代数では成り立たない。
さらには、記号的代数では計算の法則は全て証明する必要のない仮定と考えた。つまり、これこれこういう条件を満たすものが掛け算である、という現在の公理的な定義に近くなった。実際、記号的代数は、群、環、体やブール代数など現在の抽象代数学の先駆けとなるものであると言われている。
ところが、ここで問題が一つ生じる。有理数(分数)の取り扱いである。有理数は負の数などと違って、古来より数であった。しかし、ピーコックの算術的代数では、対象を自然数と限ったために、有理数は排除されてしまう。そうなると、算術的代数はあまり使えないものとなってしまう。かといって、算術的代数の対象を有理数全体にするわけにはいかない。そこで、彼は、
1。掛け算を式に書くときは、掛ける数を先に、掛けられる数を次に書く、
2。掛けられる数は自然数でも有理数でも構わないが、掛ける数は自然数に限る
というルールを作った。すなわち、積
$$
A \times B
$$
において左の掛ける数 A は必ず自然数、右の掛けられる数 B は分数でも自然数でも構わないとした。おそらく、多項式をヒントにして掛け算の順序を決定したと思われる。なぜなら、多項式で各項は係数 x 変数(の冪)の順番で書かれるからである。この時、係数は未知数の個数であるからので、整数であるが、変数は整数だけでなく有理数を表すこともある。この書き方は16世紀にドイツの古典学者ウィリアム クシランダー が、文字の左に数を置いて、その文字の倍量や半量を表すようになったのが最初であると考えられている(Jeff Oaks, François Viète’s revolution in algebra, Springer, 2018)。
$${A times B}$$で、$${A}$$ が整数で、$${B}$$ が整数でない有理数とすると、
$$
B \times A
$$
は、左にある数 $${B}$$ が整数でないので、ピーコックのルールに反し、存在しない。それゆえ、
$$
A \times B = B \times A
$$
は成り立たないということになる。つまり、算術的代数では交換法則は成立しない。
ピーコックの考え方を基にすれば、算術的代数で交換法則が成り立たないケースがあるというのは、記号的代数で交換法則をルールにする必要はない、ということでもある。ピーコック自身が交換法則の成り立たない掛け算を定義できる数の着想を得ていたのかもしれない。1842年に、アイルランドの数学者 ウィリアム ローワン ハミルトンが4元数の着想を得た。4元数は複素数の拡張で、交換法則の成り立たない数である。現在では3Dグラフィックスの分野で用いられる技術の基本となっている。もし、ピーコックが算術的代数と記号的代数を分けていなかったら、ハミルトンの着想を意味のないものとして捨てられていたかもしれない。
11. 日本はピーコックの考え方を導入していた可能性
日本における掛け算の式の順序の導入は、おそらく、ピーコックの考え方が取り入れられと思われる。明治初期の数学者でのちに文部大臣になった、菊池大麓は、1870年頃にイギリスに留学した。帰国後は、日本の数学教育、特に初等教育に力を入れた。ウィリアム キングドン クリフォードの著作を「数理釈義」に訳し、日本の教育者にその内容を講義している。クリフォードはイギリスの幾何学者で、ピーコックの影響を受けている。のちに、クリフォード代数という4元数をさらに一般化した、交換法則の成り立たない数を作った。従って、ピーコックの掛け算の式の書き方は「数理釈義」に含まれていた可能性がある。「数理釈義」の内容について書かれたものはほとんどないので、今後の研究が必要であ
なぜ日本で掛け算の順序がイギリスとは逆になった理由は、今の所、判明していない。わさっき氏や高橋氏のブログでは、歴史的な経緯も書かれているが、ピーコックには触れていないので、(菊池が持ち込んだと仮定して)そこから昭和の初めの頃までに何かしらの断絶があったと思われる。
12. 数学の原動力は常識を疑うこと
白川氏は「世の中を発展させるスーパーテクノロジーに数学がなり得たのは、世界のありようを言葉を使わずに表現できるからだったと思うのだ。そこには解釈やらニュアンスやら意志やらが介在する余地がない。客観的な記述」と書かれている。数学がこのよう形式的体系になったのは、ピーコックが代数学を記号に意味を持たせる算術的なものとそうでない記号的なものの2つに分けたことから始まっている。すなわち、掛け算の書き方に順序を導入し、交換法則を否定したことが、数学を「世の中を発展させるスーパーテクノロジー」にしたとも考えられる。
19世紀のドイツの数学者、ゲオルグ カントール は「数学の本質はその自由性にある」といっている。カントールの考えた超越数が、当時の常識に反すると、カントルが精神を病むくらいに批判されたときの言葉である。従って、この言葉における「自由」とは、「表現の自由」のような何を言っても何をやっても良い、という類の身勝手な自由ではなくて、権威や常識あるいは偏見といったものから離れて、論理的に正しいやり方で遂行するということである。この考え方は西洋哲学の父と言われる、ターレスの頃から変わっていない。
新しい数学は既存の常識とやらを疑うことから始まることが多い。例えば、非ユークリッド幾何学はユークリッドの平行線公準を疑うことから始まった。長い間、特に、ローマ カトリックから、平行線公準を疑う者は神を冒涜する者だと非難され、ヨーロッパではその研究をすることすら憚られていた。数学の2大天才の一人、カール フリードリッヒ ガウスですら、教会との軋轢を恐れて、非ユークリッド幾何学を相当なところまで研究したが、その結果を発表しなかった。しかし、ローマ カトリックの影響のあまり及ばない、イスラム圏やロシアなどでは研究が進み、ロシアの数学者 ニコライ イワノビッチ ロバチェフスキー とハンガリーの数学者 ボリヤイ ヤノシュ はそれぞれ独立に双曲線幾何学を発表した。
ボリヤイは、さらに、一歩踏み込んで、ユークリッド幾何学と非ユークリッド幾何学は互いに独立であることを証明した。つまり、それぞれ、通用する場所が違うので、どちらが正しくどちらが間違っているという議論はナンセンスなのである。
掛け算の順序問題に戻ると、交換法則は一般的には常識ではないということは既に述べた。もし仮に、常識だったとしても、それを押し付けることは、数学の発展の上から言って有益ではない。
数学史的には、式を書く時には順序があるというのは、式の構造を他人とシェアすることができるようにすることが目的なので、常識ではない。一連の騒動で、教師たちは、掛け算の式に順序ができた理由を全く知らず、ただ単にそういうものであると強制しているように過ぎないという印象を持たされる。確かにこれでは、順序反対派を納得させる要素は全くない。
13. 掛け算の式を書くときに順序を定めることは、学習意欲を阻害するか
再び、順序反対派の主張に耳を傾けてみると、全ての方が子供たちの学習意欲を削ぐと書かれている。黒木氏は彼のブログ(http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20101123Kakezan.html)で、Y君という支援学級に通う子が、掛け算の式には順序があると教わり、学習意欲が削がれた、という例を出している。しかし、支援学級に通う子供は、特別なケアが必要なので、普通の教え方では理解できないのは当たり前である。Y君の場合は、問題に出てくる数を機械的に掛けるだけで正解を得ていたが、それが、通用しなくなったので意欲がなくなったわけである。わずか一例しかなく、果たしてこれが一般に拡張できるかどうかは疑問である。実際、学習支援を必要としない子供たちについて、教師たちの感想のようなものは多く見られたが、学習意欲が削がれたかどうかの調査がなされたという報告は皆無であった。
黒木氏はまた、掛け算の式の書き方の順序で理解度を測る方法がよろしくないと言っているが、これは、Y君の例では、指定された順序通りに書いていないのは、問題を理解していなかったということだったので、よろしくないということはない。
OECDによる生徒の学習到達度調査(https://www.oecd.org/pisa/publications/PISA2018_CN_JPN.pdf )に、言語、数学、科学の日本の平均点の推移が載っているが、この問題が賑わった2012年以降、数学の成績は下がる一方である。OECDの分析では計算力はあるが、読解能力が劣るということである。PISAスコアが2012年以降下がっているのは、メディアで掛け算の順序問題を取り上げることでで、順序反対派の声が大きくなり、その結果、順序通りに書くという指導がなされなくなり、子供たちの方も問題文を読まなくとも正解できるようになったので、問題文を読まなくなった可能性が高い。それが、読解能力の低下に繋がっているのではないか、
どこに書かれていたのか今となっては見つけられないが、アメリカでは順序など気にしないという記述もあった。この方は、アメリカのPISAの成績をご存じないのだろうか。
まとめ
1。式を書くときには順序がある。それは、書き手だけでなく、読み手も式の構造が理解できるようにした、数学の文法というべきものである。掛け算も式に書くときには、何がかける数で、何が掛けられる数であるかを、はっきりさせた上で、式を書く必要がある。それが、掛け算の順序を定めた動機であると考えられる。
2。イギリス式では掛ける数を先に書くが、日本式では掛けられる数を先に書くという違いがある。どちらが正しくて、どちらが間違っているという類のものではない。しかし、個人的には、多項式の項の書き方に準ずるイギリス式が良いのではないかと思う。
3。交換法則が成り立つというのは常識ではない。代数を論理的に構築していく上で、掛け算の交換法則が成り立たなくなるのは必然であった。
4。子供たちの発達過程において、掛け算の交換法則が成り立たないと意識することがある可能性がある。
5。掛け算の式を書くとき順序を意識しないと、問題文を読まなくなるので、読解力が下がる可能性がある。
参考文献(本文中に示さなかったもの、順不同)
George Peacock (1791 - 1858) - Biography - MacTutor History of Mathematics, https://mathshistory.st-andrews.ac.uk/Biographies/Peacock/
メタメタの日 https://ameblo.jp/metameta7/
わさっきhb https://takehikom.hateblo.jp
岩波 数学辞典 第2版
菊池大麓(数学者) 西洋数学と共に持ち帰った紳士の精神 https://www.mitsubishielectric.co.jp/fa/compass/lectures/pioneers01/report.html
Alexander McFarlane, Lectures on Ten British Mathematicians, 1916, London, Chapman and Hall
吉田 奏介、数学史の一端として~記号の話
斎藤憲、数学史から見た数学教育、数理解析研究所講究録 (2012), 1801: 38-43
塚原久美子、数学史をどう教えるか、東洋書店
一松信、数学史をいかに数学教育に活すか?、数理解析研究所講究録 (1998), 1064: 108-113
溝口達也、算数・数学における数学教育の活用
George Peacock, A Treatise on Algebra (J. & J. J. Deighton, 1830).
Cajori Florian, A History of Mathematical Notations, Dover, 1993
Cajori Florian, A History of Mathematics, A McMillan Company, 1909
野村恒彦、ジョージ・ピーコック「代数学」序文について
