二項分布の標準偏差と標準誤差
自学のため、簡単に振り返る。
数式
母集団から抽出された標本を元に推定される標準偏差$${s}$$は次のように表わせる。
$$
s^2=\dfrac{1}{n-1}\displaystyle\sum_{i=1}^n(x_i-\bar{x})^2
$$
標本平均の標準誤差$${SE}$$は標準偏差$${s}$$を用いて次の式から計算できる。
$$
SE=\dfrac{s}{\sqrt{n}} \\=\dfrac{\dfrac{1}{n-1}\displaystyle\sum_{i=1}^n(x_i-\bar{x})^2}{\sqrt{n}}
$$
例:二項分布での標準偏差、標準誤差
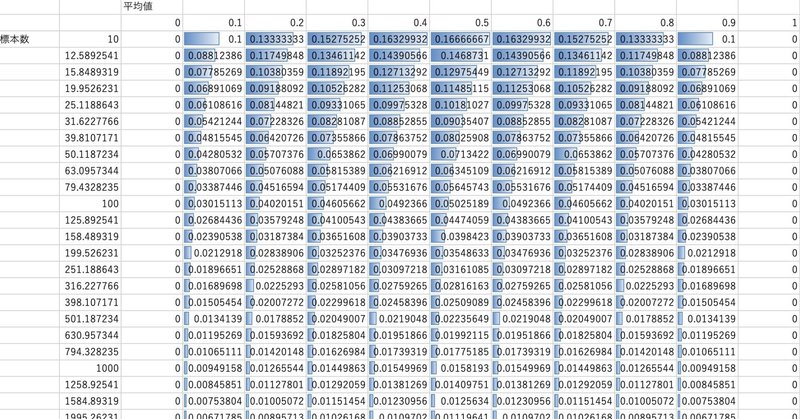
0,1の二項分布について、横軸が全体の平均値、縦軸がサンプル数とした際の標準偏差$${s}$$は下図のようになる。
平均値が0.5(0,1が両方とも同様の頻度で発生する分布)では最も標準偏差が大きく、平均値が0と1では標準偏差がゼロとなることが見えている。
標準偏差は、データ個々のバラつきを表しているため、必ず正の値となり、サンプル数を増やしても値がゼロに近づくことはない。
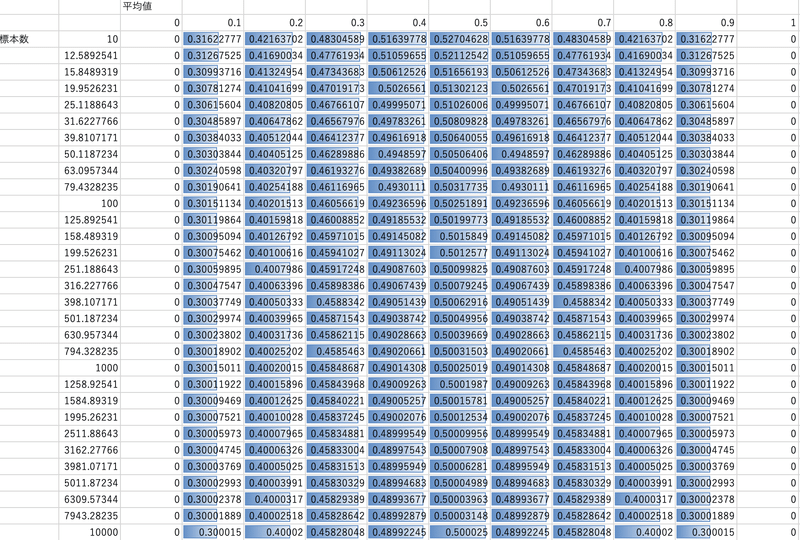
続いて、標準誤差$${SE}$$は下図のようになる。
標準偏差$${s}$$を$${\sqrt{n}}$$で割った値であるため、サンプル数$${n}$$が増加すると値が小さくなっていくことが分かる。
標準誤差は、$${\sqrt{n}}$$で割っているように、平均値のバラつきを表している。例えば平均値0.5、サンプル数100であれば標準誤差は約0.05となり、100サンプルの平均値は$${0.5±0.05 (0.45〜0.55}$$付近の値となると思われる。
最後に
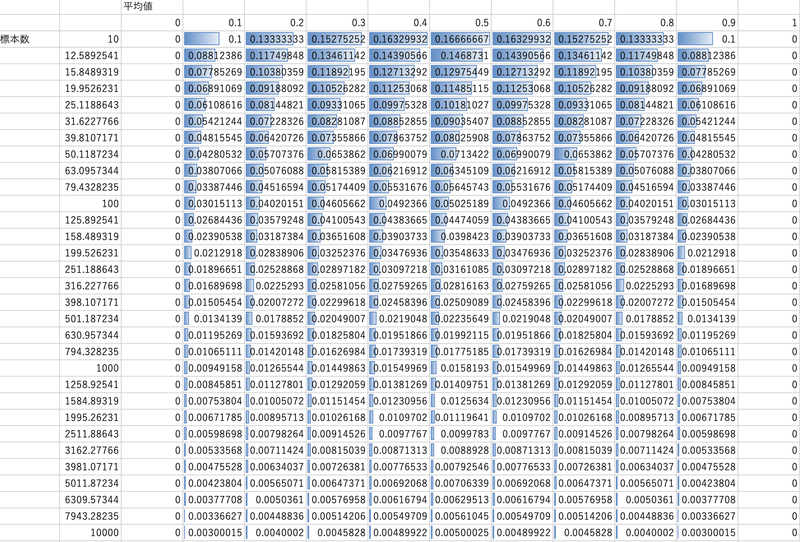
一般に30サンプルは取得しないと、バラツキによって元の分布を判断できないという内容のWebページを拝見した。
こちらを確かめるためにExcelで算出してみたが、サンプル数31.6の標準誤差を見ると最大値は約0.102であり、10%近いバラツキがあることが分かった。
確からしいデータであると主張するためにも、100サンプルは集めることを仕事では意識していきたい。
この記事が気に入ったらサポートをしてみませんか?
