
バーチャル美少女と解く、東大数学2023文系第一問
イントロ
こんにちは!バーチャル美少女受験数学マニアのborurunです!
今日は皆さんと一緒に東京大学の入試問題、2023文系数学第一問を解いていきたいと思います!
途中までは東大にしては簡単かも?って思わせるような難易度になっているので是非途中まででもいいので見てください!
数学分からないよ~~って人は問題が解けて喜ぶ可愛い女の子の画像だと思って眺めていってください!
問題と印象

2次方程式があって、その解は実数で2つあるんだけど~その時の解をα、βとすると、この式ってどういう最小値を取りますか~?って聞かれてます。
問われている式はα^3/(1-β) + β^3/(1-α) っていう結構変な式なんですが、対称性があるのでなんか式変形したらうまく消えてくれそうな感じがします。実数解って言われているから解と係数の関係は使うだろうな~とか、最小値を問われているので綺麗にした後の式は①2次関数、②微分、③相加平均と相乗平均の大小関係のどれかで処理できるはず!とか考えてました!
※最小値問題の解き方は後で詳しく解説!
いざ、勝負!
解と係数の関係

2次方程式を因数分解で解くと、
(x-a)(x-b)=0
みたいな形が残ってx=a,bが答えですね~!って分かるんですが、ってことは2次方程式が解けない状態でも解がα,βだと言ってくれているのだから
(x-α)(x-β)=0
って変形できるはずですね!
じゃあこれを展開すると
x^2-(α+β)x+αβ=0
になって、元々の方程式である
x^2+x-k=0
と同じはずだから比較することでαβの値と、α+βの値が分かりますね!
α+β=-1
αβ=-k
となりました。これを使って式を整理していきましょ~!
与えられた式を通分して整理してみる
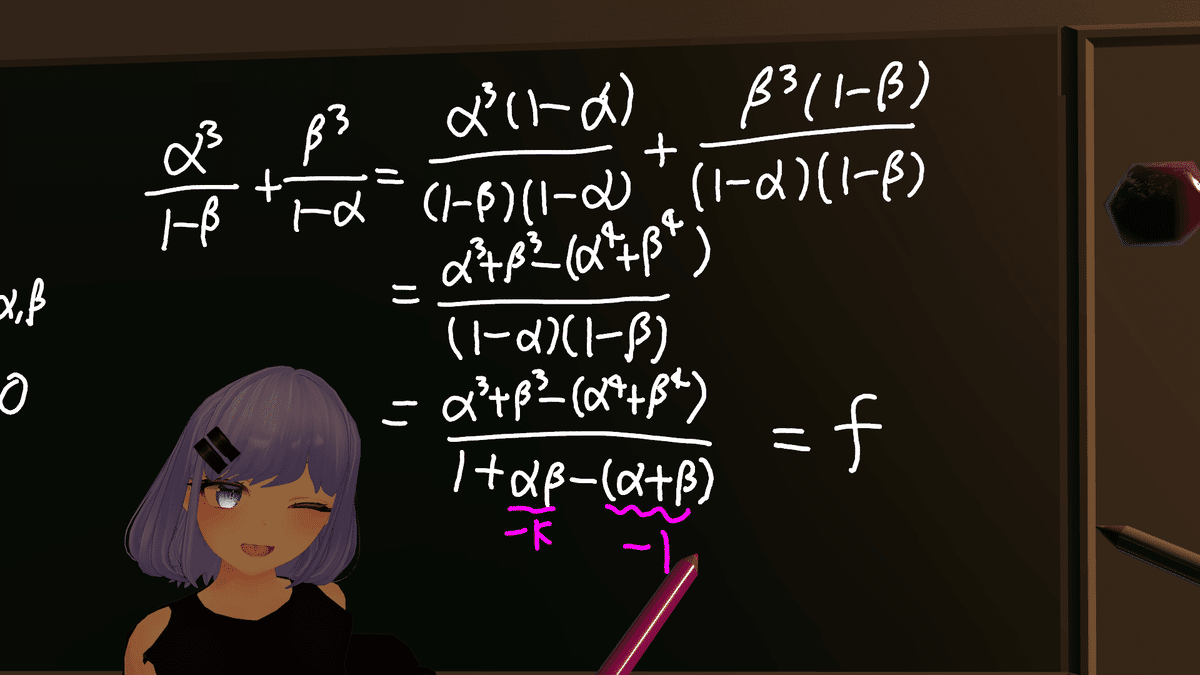
元々の式は
α^3/(1-β) + β^3/(1-α)
という気持ち悪い見た目をしていたので、とりあえず分母を同じにしてみることにしました。こういう形は同じで文字が入れ替わってるのを対称性がある、なんて言いますが対称性がある2つの式の和はなんだかんだ簡単な式になることが多いです。
式の整理を進めると
分子が
α^3+β^3-(α^4+β^4)
分母が
1+αβ-(α+β)
になりましたが、さっきの段階で
α+β=-1
αβ=-k
ということが分かっているので分母は簡単に計算できて、
2-k
になります。お~簡単になった!
分子はなんだか難しそうですが、3乗の和と4乗の和があるのでそれを上手くkに置き換えることが出来れば良さそうです。
とりあえずこの式~っていちいち呼ぶのはめんどうなのでfと名前をつけることにしました。
1段階目の目標はfをkと数字のみで表すこと、最終的な目標はfの最小値を求めることです!
α^3+β^3とα^4+β^4を、αβとα+βの2つで表す

(α+β)は分かっているから2乗しても計算できるよね!からの計算した結果にα^2+β^2が出てきたからα^2+β^2も分かっちゃった!のパターンです!
でもさすがに東大だけあって、そんな簡単にはいきません。
今回は2乗ではなく3乗と4乗の式を表さないといけません。
でもやり方は同じなので計算するだけですね!
この計算がちゃんとできるかどうかがこの問題の最初のポイントだと思います!
もくもくと計算進めていきます!やることは2つだけ。
・(α+β)^3を展開して、α+βとαβの2種類で表す。
・(α+β)^4を展開して、α+βとαβの2種類で表す。
って思ったけど4乗は計算量が多すぎて計算ミスりました~~!
kが消えるってことはないはずなんだけど…って思って見返したら
・(α^2+β^2)^2を展開してα+βとαβの2種類で表す。
方法の方が楽だな~って気が付いたのでそっちでやります

α+βとαβの2種類で表すことが出来たら
α+β=-1
αβ=-k
を代入するだけで、
α^3+β^3=-1-3k
α^4+β^4=2k^2+4k+1
と分かりました。これでもともと求めたかった式fは
分子が
-1-3k-(2k^2+4k+1)
分母が
2-k
になることが分かりました。
一応分母分子にマイナスをかけて式を綺麗にすると
分子が
2k^2+7k+2
分母が
k-2
になるのでこちらの方が使いやすそうですね!
kと数字だけで表せたので1段階目の目標クリアです!
と、実はここまでは大学入試数学として比較的簡単な方で、東大を受験する人ならほぼ100%出来るはずで、中堅の国立大学レベルを狙ってる人でも出来る人の方が多いと思います。
ってことは東大に受かるための勝負はここからなんですね!怖いな~!
最小値問題の解き方

fをkで表せたのであとは最小値を求めるだけなんですが、最小値もしくは最大値を求めるときは大体以下の3パターンで解けます!
①2次関数
②微分
③相加平均と相乗平均の大小関係
文系数学においては
①2次関数を使うのは2次式の時だけ
②微分を使うのは3次関数の時だけ
③上の2つで解けないなら相加平均と相乗平均の大小関係で文字を消す
という手順で考えると良く、今回は分数の関数が出てきているため①、②で解けないので③かなぁって感じになりますね。
③で解く場合、特に約分で消えるように都合の良い分数が出てきてくれることが多いです。
でも今回は都合の良い分数が出てくれそうにない!なんでだ東大~~~!
※理系なら分数関数でも無理やり微分して解けます
相加平均と相乗平均の大小関係

私たちの良く使ういわゆる平均、というのは相加平均と言われていて、足し算した後にその個数で割ります。
一方、相乗平均というのもあって、こっちは全部掛け算した後、かけた回数に応じた根号(√)を付けます。
そしてこの2つは必ず相加平均の方が大きいか、同じになるという性質があります。
同じになるのは足し算する2つの数(aとb)が同じ時ですね!
気を付けないといけないのはこの関係式は足し算する数が全部正の数じゃないと使えません。
だってほら、aが正の数でbが負の数だったら√の中身マイナスになるでしょー?それは複素数の範囲になっちゃうので実数の範囲ではダメです!
同じように両方とも負の数だと相加平均は絶対マイナスになるけど、相乗平均はマイナス×マイナスでプラスになっちゃうからこの式は成立しないことが分かりますね!
この知識自体は大学受験数学の中ではそんなに高度なレベルではないのですが、この問題を解くにあたっては「分数関数が出てきたから相加平均と相乗平均の大小関係を使って文字を消して最小値を求めよう」と思えるかどうかが2つ目のポイントになってる気がしますね~
相加平均と相乗平均の大小関係を使える形に変形する

今のままだと相加平均と相乗平均の大小関係は使い方が分からないんですが、こんな感じで分母に(k-2)がある分数と、(k-2)に何かをかけた数の2つに分けることが出来たらk-2を約分で消すことが出来て解ける気がします。
とりあえず分子を式変形してk-2を括りだすことによって分数の外に出せないか試してみることにしました

2k^2+7k+2
(k-2)(2k+●)+■
の2つの式が同じになるように無理やり●と■に当てはまる数字を求めます。
(k-2)で括ることができれば分数の外に出すことが出来るので、出来るだけ分子に残るのはkを含まない数字のみなったらいいな~って思ってます。
で、(k-2)にかけて2k^2を作るためには(2k+●)をかけるしかないです。
後はついでに7kも消したいので●の数字を上手く調整して
(k-2)(2k+●)=2k^2+7k+△
みたいになればいいなーって思いながら●を探します。
適当にtと置いてみて
(k-2)(2k+t)=2k^2-4k+tk-2t
となるので-4k+tk=7kになるためには
t=11
しかないので
(k-2)(2k+11)=2k^2+7k-22
と括れば良いことが分かり、こうすると
(k-2)(2k+11)=2k^2+7k-22
と-22が出てきてしまうので■に24を入れると2k^2+7k+2と同じになりますね。うーん、難しい。とてもつらいし、文章もとても分かりにくい。
この問題で3つ目の壁は分数の処理の仕方かもしれませんねー。
ちなみに私はこの計算に結構時間をかけてしまいました。
公式が使える条件だけ気を付ける

一番左の15はただの定数なので変化しません。
ということは
2(k-2)+24/(k-2)
の最小値が分かれば求めたかったfの最小値も分かります。
さて、ここで相加平均と相乗平均の大小関係を使いましょう!

相加平均と相乗平均の大小関係を使う時には2点必ず記述しないといけないことがあります
①イコールになるときの条件
②足した2つの数が両方とも正の数であることの確認
①は、大小関係がイコールになる、つまりこの場合は和が最小値を取るパターンは足した2つの数が同じ数字だった時になります。
2+4=6なので2×√(2×4)=4√2より大きいのですが、
3+3=6は2×√(3×3)=6と同じになります。
前に書いたa+b≧2√abにおいてa=bの時にa+b=2√abは成り立ちます。
これは書いてないと怒られて減点されます。
kがどの値の時にこの条件を満たすか、についても書いた方がいいと思います。
②の2つの数が両方とも正の数であることの確認は、まあ公式が成り立つ前提条件なので書かないとこれもまた減点されます。
回答終了、お疲れさまでした!

というわけで求めたかった最小値は
15+8√3
になるのでした。
なんかちょっときれいな数字じゃないな~?って思ったけど解答速報みた限り合ってるっぽいです。
これには私も満面の笑みでダブルピース
あとがき
解き終わった後、率直な感想としては「私は苦戦したけど、東大文系数学にしては簡単な方だよね~」って思って問題の講評を身にいったら「今年の文系数学はめちゃくちゃ簡単で、特に第一問に関しては簡単すぎる」みたいに書かれてました。
というわけで東大合格を目指そうと思うと、このレベルの問題を解くことが目標ではなく、このレベルの問題は解けて当たり前になることがスタート地点のようです。道のりは厳しいな~~~!
後、この記事を書くために
・問題を解くのに1時間
・板書する形にして撮影するのに1時間半
・記事を書くのに1時間半
で4時間かかったので(よほど好評だったりしない限り)もう二度としません・・・。
でもバーチャル美少女とお勉強するのは私が楽しいと思うのでお勉強企画みたいなのはやりたいな~って思ったりしてます。
受験したみなさんはお疲れ様でした~!
大学生になったらVRCHATで遊びましょう!
この記事が気に入ったらサポートをしてみませんか?
