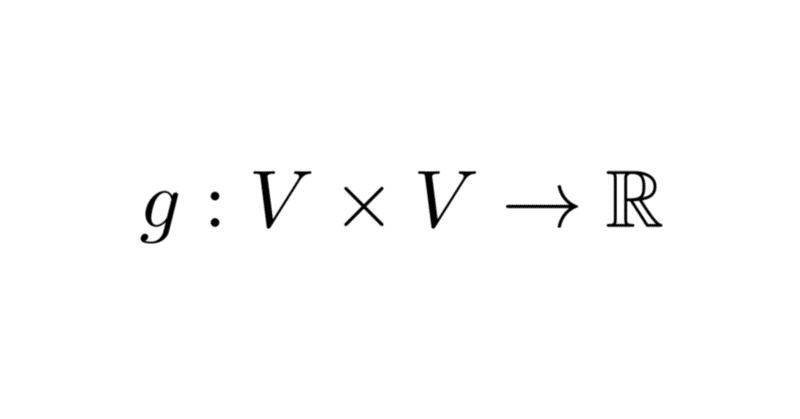
内積の（正）定値性と計量の非退化性

内積の一般化としての計量

　一般の有限次元ベクトル空間$${V}$$に対し、高校で習う$${\mathbb{R}^3}$$の標準内積

$$
\bm{x}\cdot\bm{y}\coloneqq x_1y_1+x_2y_2+x_3y_3
$$

の一般化としての内積が以下のように定義される。

定義1（内積）
$${g:V\times V\rightarrow\mathbb{R}}$$が以下の4条件を満たすとき, 内積（inner product）とよぶ.
(i) （線形性）$${\forall u_1,u_2,v\in V,\ \forall a,b\in\mathbb{R}}$$
　　$${\ g\left(au_1+bu_2,v\right)=ag\left(u_1,v\right)+bg\left(u_2,v\right)}$$
(ii) （対称性）$${\forall u,v\in V}$$
　　$${g\left(u,v\right)=g\left(v,u\right)}$$
(iii) （非負性）
　　$${\forall u\in V,g\left(u,u\right)\geq 0}$$
(iv) （定値性）
　　$${g\left(u,u\right)=0\iff u=0}$$

　(iii)の「非負性」と(iv)の「定値性」をまとめて「正定値性」と呼ぶことも多いが, 本頁では後の議論展開のためにあえて分けてある.

　さて, (i)～(iv)のなかで特に重要な性質は(iii)の非負性である。というのも内積は本来$${V}$$の元$${v}$$の"長さ"を計るための道具であり, $${g\left(v,v\right)}$$が正負どちらにもなり得る状況下ではノルム$${|v|=\sqrt{g\left(v,v\right)}}$$が定義できないからである.

　しかし物理、特に相対論や場の理論では負のノルムも許して定義を拡張した広義の"内積"が重要になってくる（計量とよばれる）. 最も馴染み深い例はMinkowski計量

$$
\eta\left(x,y\right)\coloneqq-x^0y^0+x^1y^1+x^2y^2+x^3y^3
$$

であろう.

　一般の計量（広義の"内積"）の定義は以下で与えられる.

定義2（計量）
$${g:V\times V\rightarrow\mathbb{R}}$$が以下の3条件を満たすとき, 計量（metric）とよぶ.
(i) （線形性）$${\forall u_1,u_2,v\in V,\ \forall a,b\in\mathbb{R}}$$
　　$${\ g\left(au_1+bu_2,v\right)=ag\left(u_1,v\right)+bg\left(u_2,v\right)}$$
(ii) （対称性）$${\forall u,v\in V}$$
　　$${g\left(u,v\right)=g\left(v,u\right)}$$
(iii) （非退化性）
　　$${\forall v\in V, g\left(u,v\right)= 0\implies u=0}$$

　この定義は確かに定義1（内積の定義）から「非負性」を除いたものになっていて内積の拡張だと思える. しかし定義1と定義2をよく見てみると, 最後の条件が「定値性」から「非退化性」に置き換わっていることに気づく.

　これはなぜか？

図1. 内積から計量への一般化

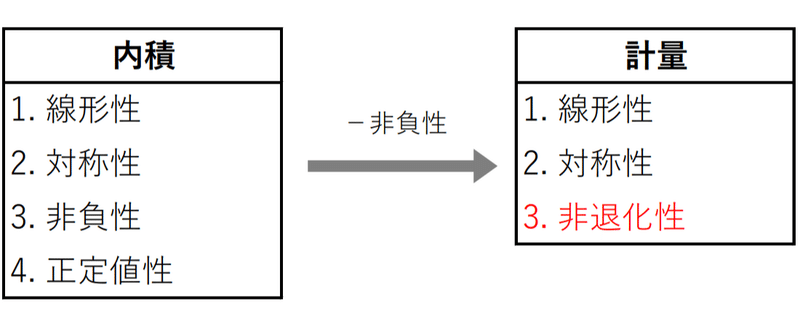
　結論からいうと, 「非退化性」は「定値性」から導かれる緩い条件である. つまり, 内積を計量へ一般化するときに「非負性」を取り除くのに加えて, 「定値性」を「非退化性」に広げたのだ。

　実際, 次に示すように内積（定義より「定値性」を有する）は「非退化性」も満たす.

命題3
内積は非退化性を満たす.

（証明）

　非退化性とは

$$
\forall v\in V, g\left(u,v\right)= 0\implies u=0
$$

が成り立つことであったので, これを示す. 矢印の左側の

$$
\forall v\in V, g\left(u,v\right)= 0
$$

を仮定したとき, 特に$${v=u}$$とすると,

$$
g\left(u,u\right)= 0
$$

となり, 定値性

$$
g\left(u,u\right)=0\iff u=0
$$

により$${u=0}$$, つまり矢印の右側が成り立つ. よって内積は非退化性を満たす ■

　命題3により, 「内積$${\implies}$$計量」が保証される.

「定値性」を緩める理由

　ではなぜ内積を計量に一般化する際に「定値性」を「非退化性」に緩めたのだろうか. それは「非負性」を外すと「定値性」自身では制限が強すぎて不都合が生じるからである.

　実際, 「定値性」を課すことは$${\bm{0}}$$ベクトルではないが長さが$${0}$$のベクトルの存在を許さないことに等しいが, 例えば特殊相対論では, nullベクトルと呼ばれる光円錐（lightcone, $${t^2-x^2-y^2-z^2=0}$$で定義される）上の$${\bm{0}}$$でないが"長さ"は$${0}$$のベクトルが重要になってくる.

図2. Minkowski時空と光円錐（Wikipediaより）

　これはあくまで1つの例における直感的な説明でしかないが, 実はより一般に, 計量に定値性を課すと内積に"逆戻り"してしまうことが示せる:

定理4
定値性を持つ計量は内積または負値内積である.

（註）
負値内積とは内積の定義で
　(iii) （非負性）
　　$${\forall u\in V,g\left(u,u\right)\geq 0}$$
を
　(iii)' （"非正性"）
　　$${\forall u\in V,g\left(u,u\right)\leq 0}$$
に置き換えたものである（"非正性"は一般的な用語ではない）. つまりベクトルの"長さ"が全てマイナスとなる"内積"である.

図3. 内積と負値内積の関係

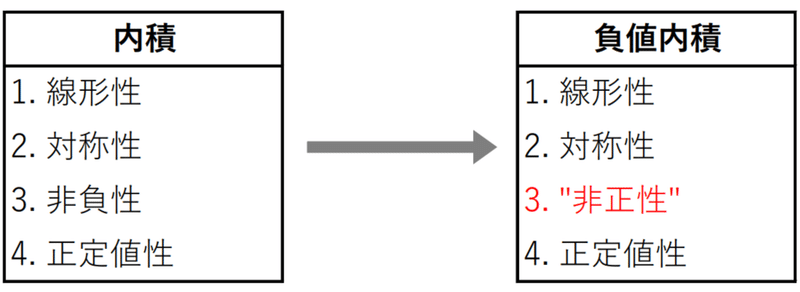
尚, 3の「"非正性"」と4の「定値性」を合わせて「負定値性」と呼ぶことも多い.

　負値内積$${g}$$に対し, $${g^{\prime}\left(u,v\right)\coloneqq -g\left(u,v\right)}$$と定義すれば$${g^{\prime}}$$は内積になるので, 負値内積を考えることは本質的に内積を考えることと変わらない.

（定理4の証明）

　背理法で示す. 計量$${g}$$は定値性を有するが, 内積でも負値内積でもないと仮定する. つまり

$$
g\left(u,u\right)>0,\quad g\left(v,v\right)<0
$$

を満たす$${u,v\in V\backslash\left\{0\right\}}$$が存在すると仮定する. 容易にわかるように$${u\parallel v}$$（平行）にはなり得ない. $${u,v}$$を適当に定数倍することで

$$
g\left(u,u\right)=1,\quad g\left(v,v\right)=-1
$$

であるとして一般性を失わない. このとき$${c\in\mathbb{R}}$$に対し,

$$
\begin{aligned}
g\left(cu+v,cu+v\right)&=c^2g\left(u,u\right)+2cg\left(u,v\right)+g\left(v,v\right) \\
&=c^2+2cg\left(u,v\right)-1
\end{aligned}
$$

と計算できるが, 2次方程式

$$
c^2+2cg\left(u,v\right)-1=0
$$

は実数解

$$
c_1,c_2=-g\left(u,v\right)\pm\sqrt{g\left(u,v\right)^2+1}
$$

をもつので$${g\left(c_1u+v,c_1u+v\right)=g\left(c_2u+v,c_2u+v\right)=0}$$である. $${u\nparallel v}$$なので$${c_1u+v=0}$$でも$${c_2u+v=0}$$でもない.

　これは定値性

$$
g\left(u,u\right)=0\iff u=0
$$

に矛盾するので, 仮定が間違っており, $${g}$$は内積または負値内積である■

　以上で内積から計量へ一般化するときに「定値性」を弱い条件（＝非退化性）に緩める妥当性を説明できた.

「非退化性」に緩める必然性

　しかしまだ疑問は残る. 「弱い条件」に緩和するだけなら非退化性ではない, 別の定値性から導かれる条件でもよかったのではないか.

　実はこの疑問にも合理的な説明が存在する.

　それは内積の場合は、定値性と非退化性が同値になるという事実に依拠する. つまり, 定義1（内積の定義）で最後の(iv)「定値性」を「非退化性」に置き換えたもの（＝計量の定義に「非負性」を追加したもの）が全く同値な定義になるのだ.

図4. 正定値性と非退化性の関係

　「定値性$${\implies}$$非退化性」は既に命題3で示しているので, 逆の「非退化性$${\implies}$$定値性」が, 「非負性」

$$
\forall u\in V,g\left(u,u\right)\geq 0
$$

を満たす計量の場合に成り立つことを示そう（一般の計量では必ずしも成り立たない）.

命題5
非負性を満たす計量$${g}$$は内積である.

（証明）

　$${g}$$が定値性

$$
g\left(u,u\right)=0\iff u=0
$$

を満たすことを示せばよい. $${u\in V}$$に対し$${g\left(u,u\right)=0}$$が成り立つとする. 任意の$${v\in V}$$と任意の$${t>0}$$に対して, 非負性より

$$
\left\{
\begin{aligned}
\frac{g\left(u-tv,u-tv\right)}{t}\geq 0 \\
\frac{g\left(u+tv,u+tv\right)}{t}\geq 0
\end{aligned}
\right.
$$

が成り立つ. $${g\left(u,u\right)=0}$$を用いて2式それぞれで左辺を展開すると,

$$
\left\{
\begin{aligned}
-2g\left(u,v\right)+tg\left(v,v\right)\geq 0 \\
2g\left(u,v\right)+tg\left(v,v\right)\geq 0
\end{aligned}
\right.
$$

ゆえに

$$
-\frac{t}{2}g\left(v,v\right)\leq g\left(u,v\right)\leq\frac{t}{2}g\left(v,v\right)
$$

$${t>0}$$は任意だったので

$$
g\left(u,v\right)=0
$$

となり, $${v\in V}$$も任意だったので, 非退化性より$${u=0}$$■

　上の証明をじっくり読めばわかるが, 非負性を有さない一般の計量は内積にはなるとは限らない（証明の1行名で非負性を使っている点に注目！）.

　命題5で注意してほしいのが, 「非負性 + 定値性（＝正定値性）$${\iff}$$非退化性」ではなく, 「非負性」の下で「定値性$${\iff}$$非退化性」となるということだ. つまり

$$
\text{非負性 + 定値性（＝正定値性）}\iff\text{非負性 + 非退化性}
$$

が正しい.

まとめ

　このように「非負性」の下では「定値性」と「非退化性」は同値条件なのである（命題5）. そして非負性の仮定を外したとき2つは同値でなくなり, 「定値性$${\implies}$$非退化性」という関係になる（命題3）. この場合「定値性」では強すぎる（定理4）ため, 一般の計量の定義では「非退化性」に緩めるのだ.

※ 内積の定義で初めから「定値性」ではなく同値条件である「非退化性」を書いておけば, 内積が計量の一般化になることが定義を見ただけで分かるようになるのではないか, という疑問を持つ人がいるかもしれない.

　これについては最初に定義した人に聞かなければわからないのだが, おそらく内積を"長さを図る道具"として直感的に捉えたとき, 「$${\bm{0}}$$ベクトル以外の長さは$${0}$$にならない」ことを述べている「定値性」の方が「非退化性」より断然イメージしやすかったからではないかと思っている.