
パズルノート大発掘会
この記事はペンシルパズル Advent Calendar 2023 12/19分の記事です。
こんにちは。うまや天国です。
今回はパズルノート振り返りということで、パズルを紙面上で作る時に使っていたノートを見返してみます。
自分はメモが必要なパズルだったり、ぼんやりしたアイデアとかをノートに書き残す派なので、それらがこのまま忘れ去られないよう発掘して晒し上げるのが今回の目的です。

約6年間で使ったノートは計4冊です。
幼少期に学校で使っていたノートの余りを流用しているため、自分の名前とか科目名とかが書いています。
1冊目

表紙から察するに小6の時の計算ドリルに使う予定だったノートを流用しているようです。
初めて作ったパズル

現存する作品のうち最古のパズルはぬりかべでした。
「ふつう」と書いてますが普通に難しいです(完全に難易度詐欺)
やっぱり最初は「唯一解やしええか」の気持ちで過剰に難しい問題を作ってしまいがちです。


「芽」というタイトルがつけられていました。初めて名前を付けたパズルのようです。例にもれずサイズの割りに難易度が高いです。
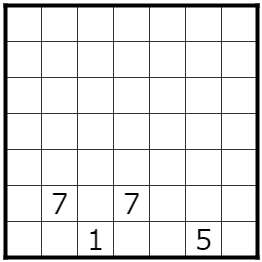
波及効果
表出ゼロ波及効果を発掘しました。
パズル作りたてやのにすごいな(自画自賛)

三角迷路
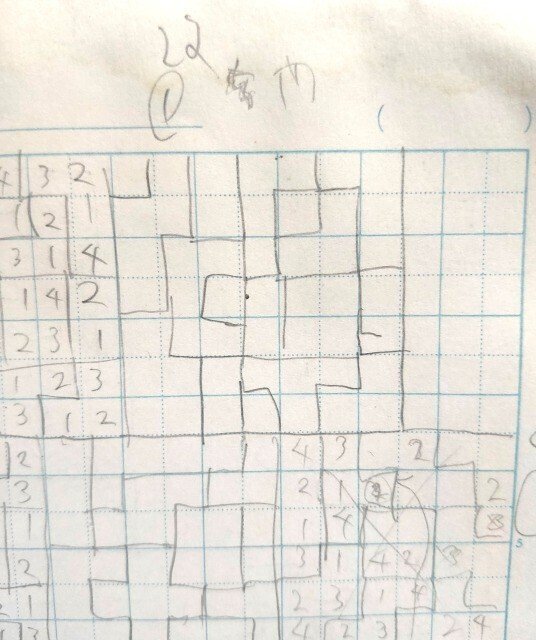
初のオリジナルパズルである三角迷路の作成過程です。
ルール等は過去記事「ペンパ同好会で作ったオリジナルパズルの歴史」をどうぞ↓
https://note.com/umayainferno/n/na37b34da2a1d

5cm四方にぐちゃぐちゃ書いてます。
月か太陽

割り切れマス

このころは問題同士の間隔をあけていないせいで視認性が悪いです。
京都の通りスケルトン
大学の新歓にピッタリすぎて配りまくった思い出のパズルです。
宗教上の理由で猪熊通と綾小路通が交差しています。
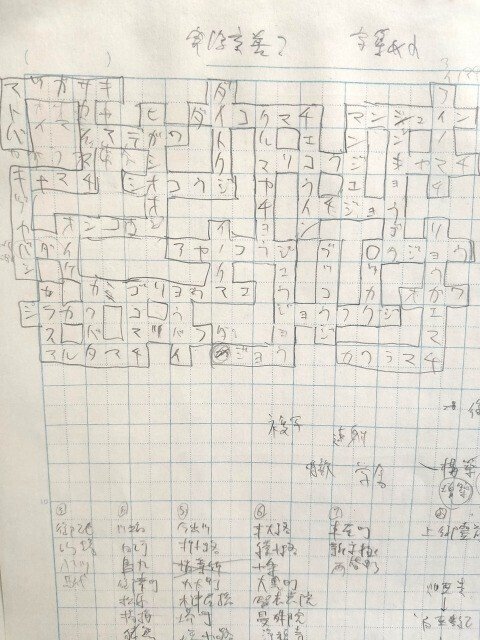
没熟語迷路

SからGまでマスの中央をタテヨコに動いて漢字をちょうど4つ通り、熟語を作ります(同じマスは2度通れない)。
唯一解じゃなさそう等もろもろの理由で没です。
想定解はR7C3, R3C3, R2C6, R5C5を順に通ります。
連番窓口
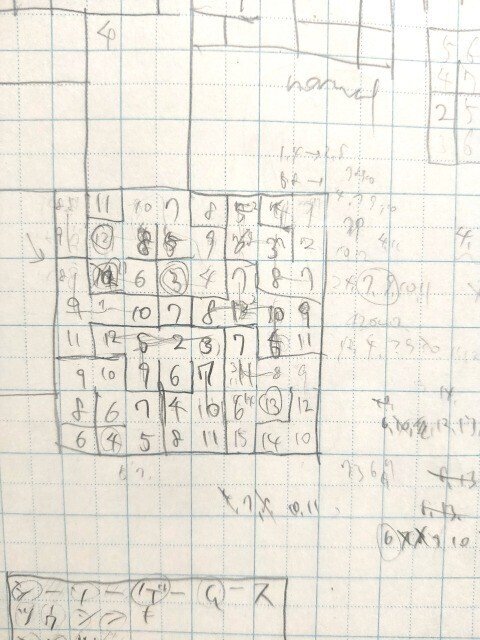
個人的に制約の強いパズルは紙面の方が色々メモできて作りやすいです。
2冊目

この辺りからオリジナルパズルのアイデアメモが増えてきます。
ぬりみさき

ぬりみさき考案時のメモです。
「港湾開発」とか「ミサキン」とかの名前案もありましたが一番無難なのにしました。
シンメトリー迷路
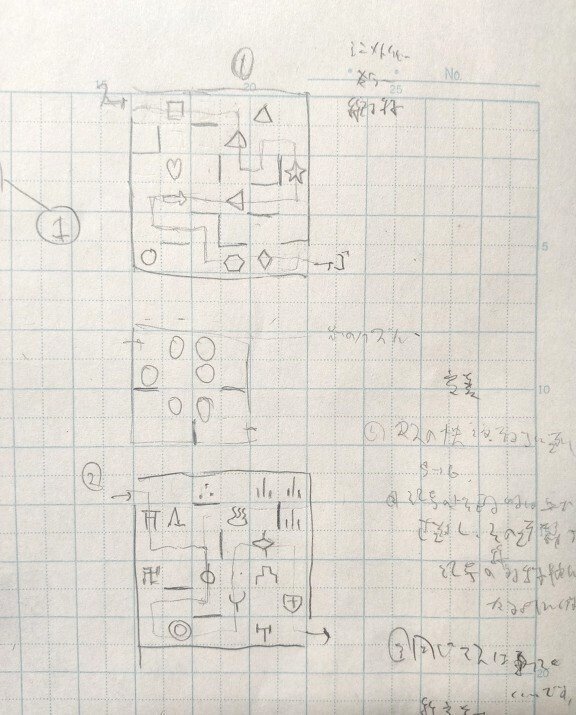
手書きだと味がありますね。
連番窓口
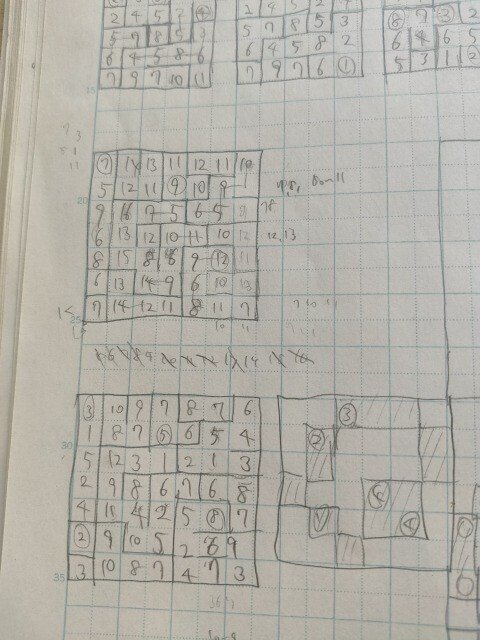
連番窓口を発掘しました。
ちょうどいい感じだったのでパズスクに上げます。
ペンシルズ

ペンシルズの上に鉛筆シールが貼られていました。
ノートに備え付けのやつをふざけて貼っています。
月か太陽美術館
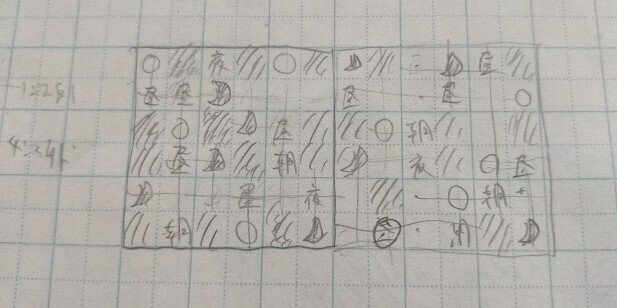
・美術館で明かりの代わりに月か太陽を置く
・日光に照らされる部分は朝に、月光に照らされる部分は夜になり、日光と月光の両方に照らされる部分は中和して昼になる
世界観は好きなんですが今見ると実質的にRGB美術館
オリジナルパズルメモなど
こんなパズルが解きたいなーという願望だけの、パズルですらないものも交ざっています

ルールは謎

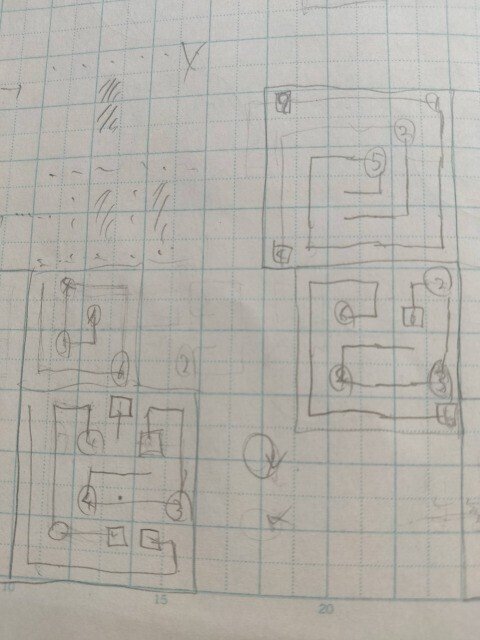
「外回り蚊取り線香」とメモがあった
もしかしてネットにあった問題を写しただけか・・・?

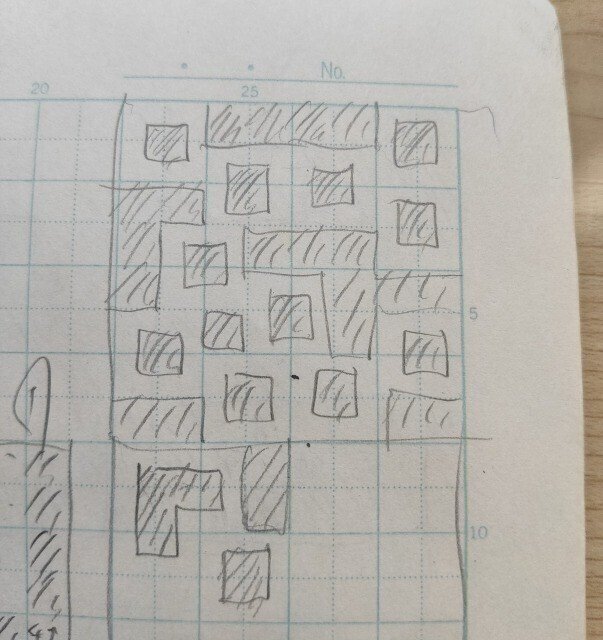
各領域内は連番、△▽はそれぞれ領域内最小最大

恵方巻をイメージ
鋭角に曲がらない、□は直角
鋭直鈍ループの存在を知ったのはしばらく後のことだった
各領域についてループの内側になる面積はちょうど半分
中央や右下が破綻している
3冊目

このころからA4ノートになります。
B5の頃はジャイアント(31×45)を作る時は罫線から盤面がはみ出てました。
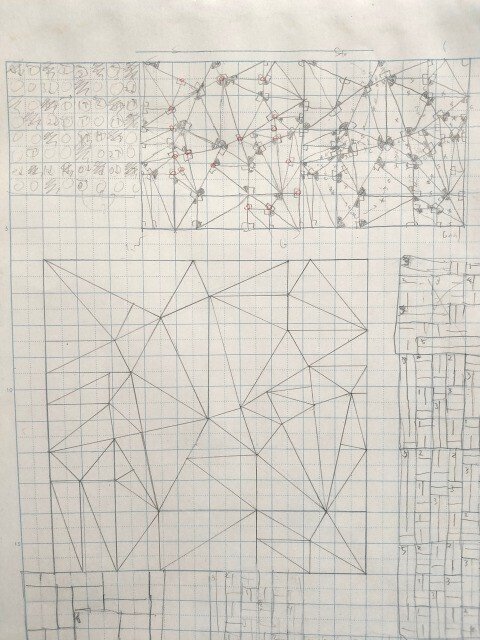
扇迷路
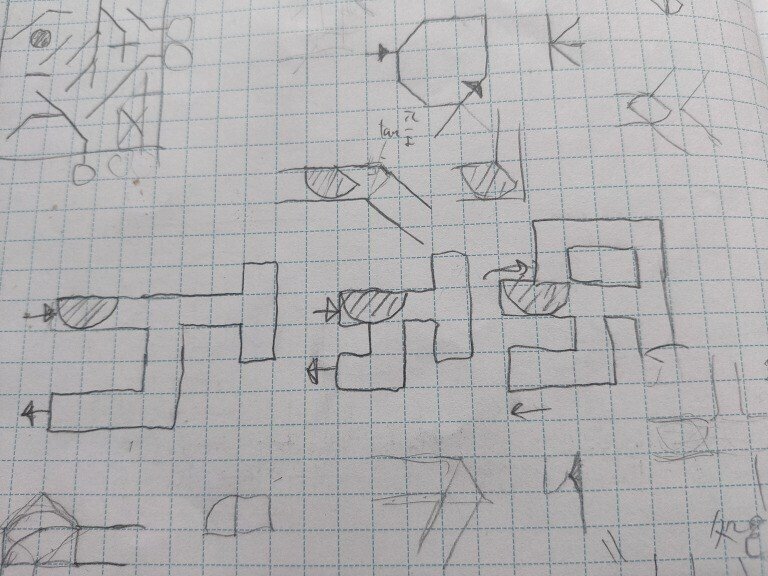
半円の扇形をスタートからゴールまで運ぶパズルです。
ソファ問題から着想を得ています。

こちらは135°の扇形バージョンです。
斜め線が使えて楽しそうです。
プログラミングスキルがあればこういうパズルゲームも作ってみたいですね。
ミッドルーム

ミッドループに領域の概念(□は部屋に入ってから出るまでの中点)を入れています。
通るマスが前半か後半かとかを表出しても面白そうです。
四国に切れ
「ペンパ同好会で作ったオリジナルパズルの歴史」ラストの問題です。
チャージシャトル

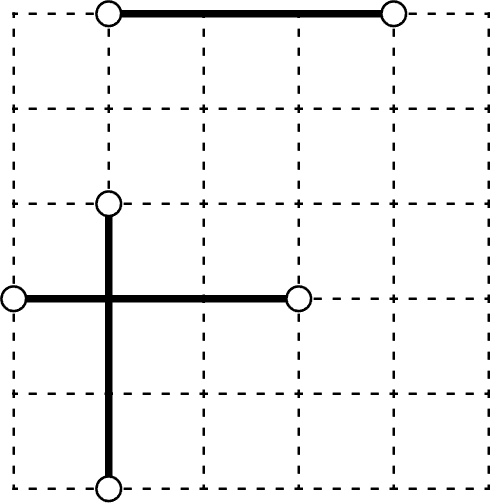
ルール:
・点線上に線を引いて交差ありループを1つ作る
・○で必ず曲がる
・あらかじめ表出されている直線は全て使い、表出の直線を除き線は全て曲がる
線が曲がりまくるパズルええなあと思っていた時に作ったものです。
直線部分がめっちゃ速く走るロケットで、曲線部分が燃料切れみたいだったので「チャージシャトル」と呼んでいました。
意外と細かい部分が決まりづらいです。
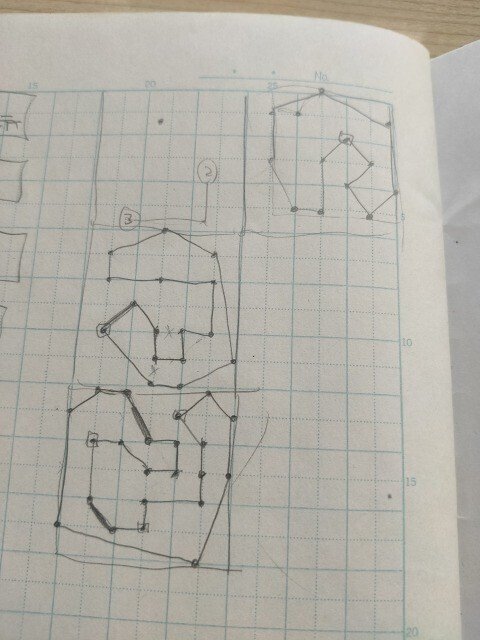
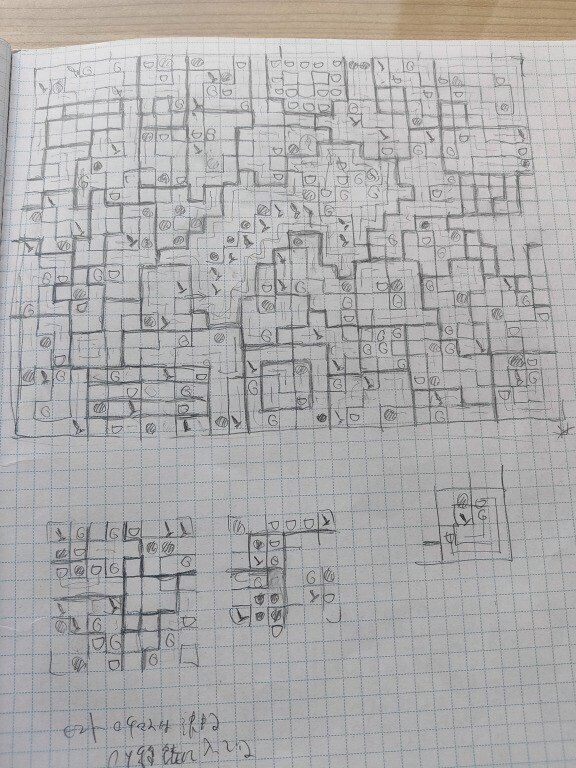
渦巻き

カーブデータで渦巻を入れる時の最小マス数を調べています。

予想ですが右上の図のような形でマス数が増えていきます。
↓の問題にも活用されています、よろしければどうぞ。
https://puzsq.logicpuzzle.app/puzzle/2542
シンプルガコの分類

シンプルガコの数字の入れ方は実質何通りあるか考えたときのものです。
3以下は自明なのですが4から急に地獄になった記憶があります。
行や列の入れ替えで移りあうものを同一視したり、"連結"なものだけを探すと、4 in 4×6は2通りみたいです。
(ここでいう連結は、数字の入っていないマスを氷としたとき、全ての数字マス同士で互いに移動できるみたいな意味です)
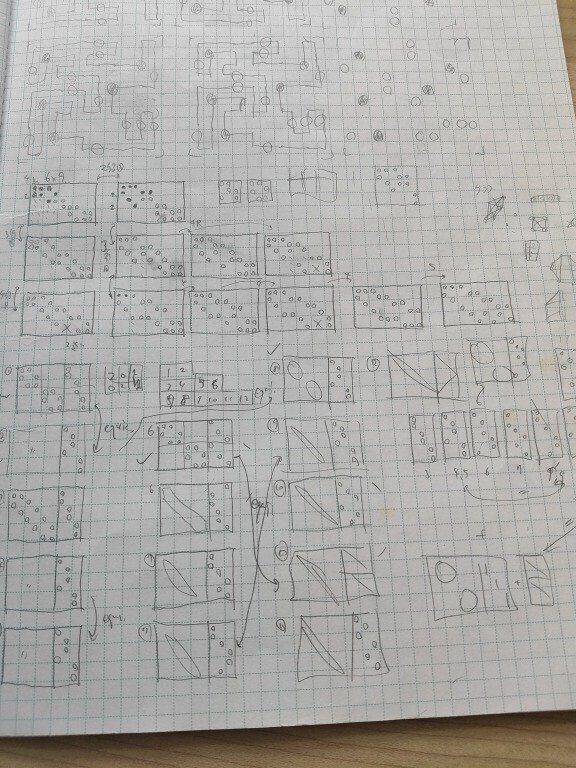
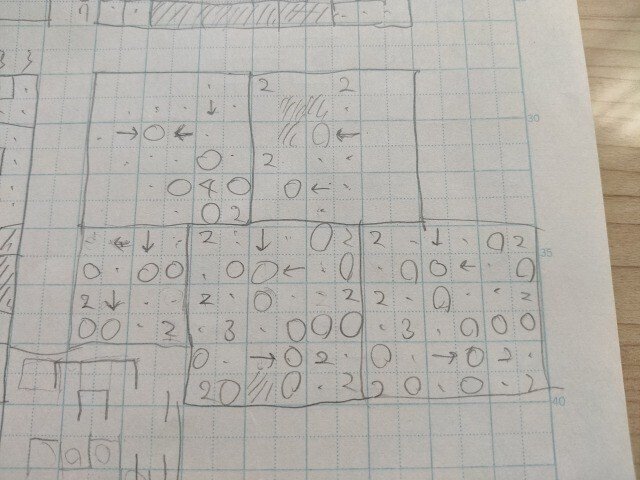
全表出スリリン
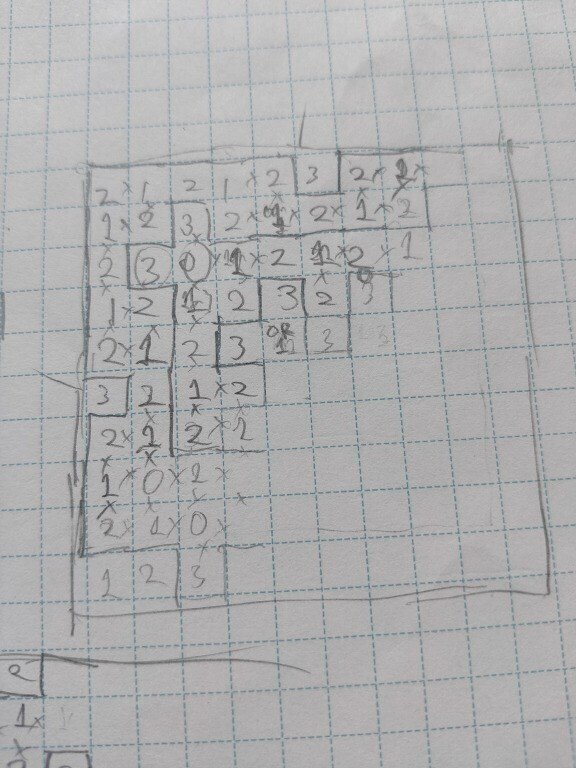
「スリリンの盤面であって、数字を全表出した時に同じ数字がタテヨコが隣接しないようなもの」を探していた時のものです。
上の盤面では同じようなパターンを繰り返し始めて諦めています。
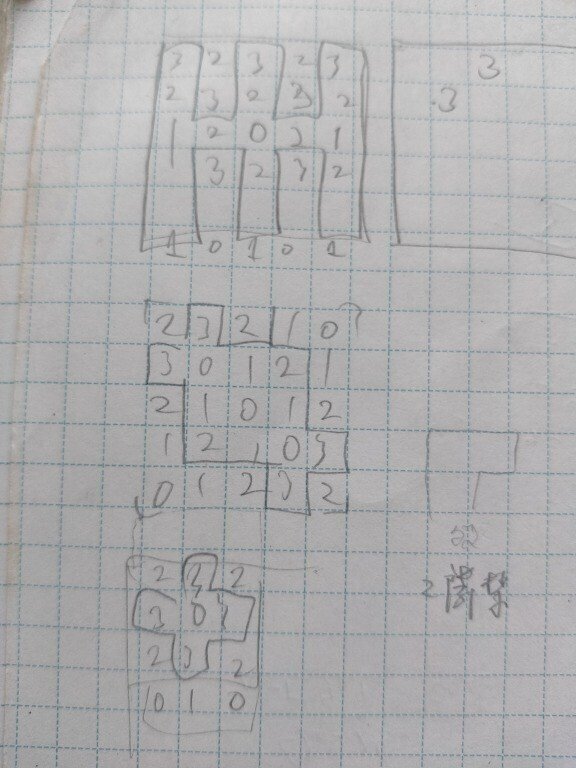
3×3や5×5だといくつか見つけました。
一番上の例は5,6,7×(2n+1)まで拡張できます。
その他


右下のように星同士の線が鋭角にならないルールで何かできそう
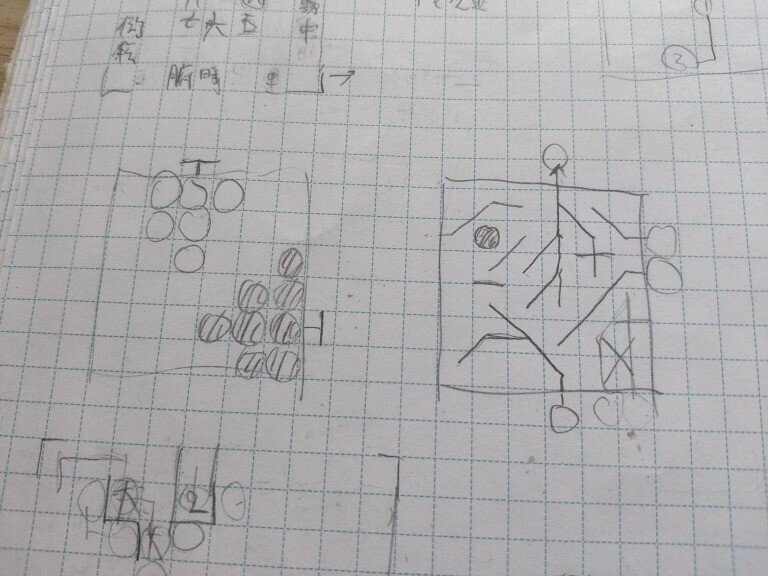
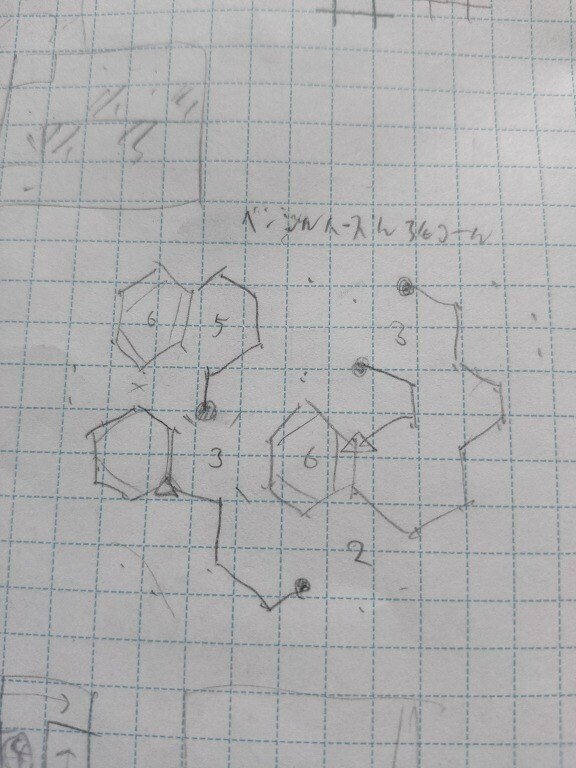
ベンゼン環を使ったパズルに「ベンジルパズル」と名付けるのが夢です

T字をなべぶたと呼びたい

各直線は黒丸、十字白丸、線一本白丸の3種のダンゴを通る(画像中央上)
左下のように黒ダンゴと十字ダンゴ同士が交互につながりまくることに気づきボツ
4冊目

このあたりから数学的な考察が増えてきます。
雑に扱いすぎて4つに分解してしまいました。
タタミサキ

1×n領域に分割、○は領域の端っこ、数字は領域の面積、境界十字禁
何か見覚えあるし既出だったかもしれない
対辺迷路
これです↓
「たいへん迷路」を作りました。
— うまや天国 (@ardjmk10Dqag) August 20, 2022
対辺同士を飛び移ってゴールをめざす感じです。 pic.twitter.com/GERGSXtD79
PC上で清書するのが一番大変でした。
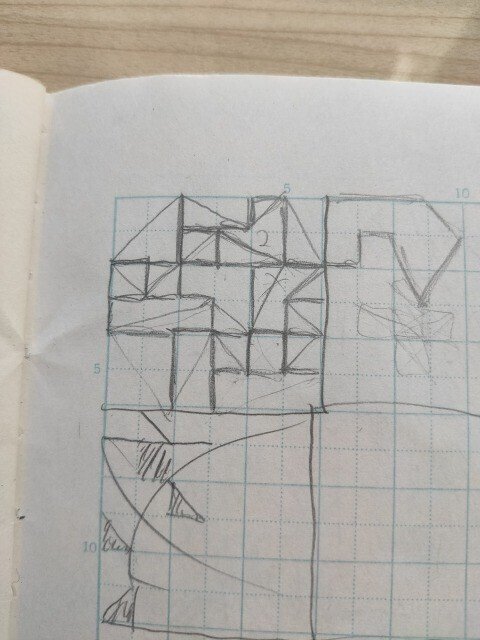
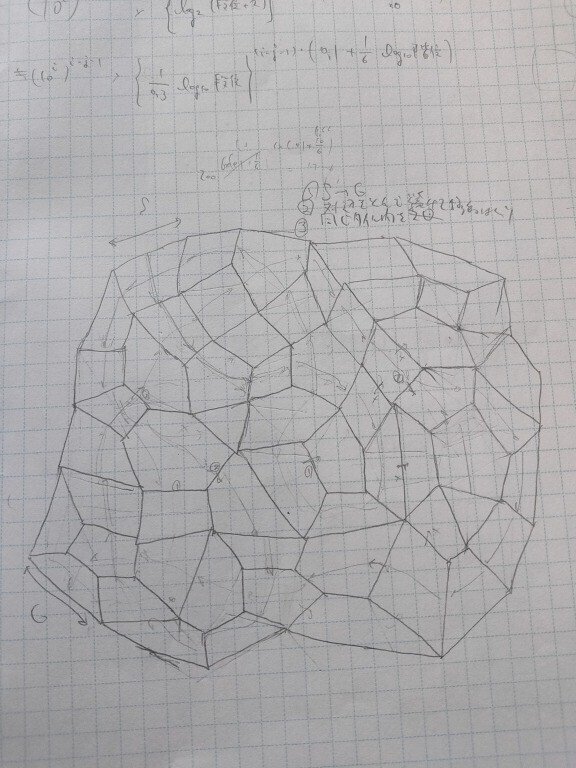
ポリスティック

ポリスティックについての記事「双対ポリスティック」を書いていたころの分類の様子です。
そもそもペンタスティックの一覧がみつからなかったので自分で調べた覚えがあります。

①ポリスティック→ポリオミノへの変換としてスティックの各頂点をモノミノへ置き換える
②ポリオミノ→ポリスティックへの変換としてD変換の逆像を1個取る
とした時、①②を交互に繰り返すとどうなるか調べたものです(D変換は上記記事「双対ポリスティック」参照)。
②の変換は写像にならない(逆像が最大2個になる)ので収拾がつかなくなったりする可能性もありますが、基本的にどこかで止まる気がします。
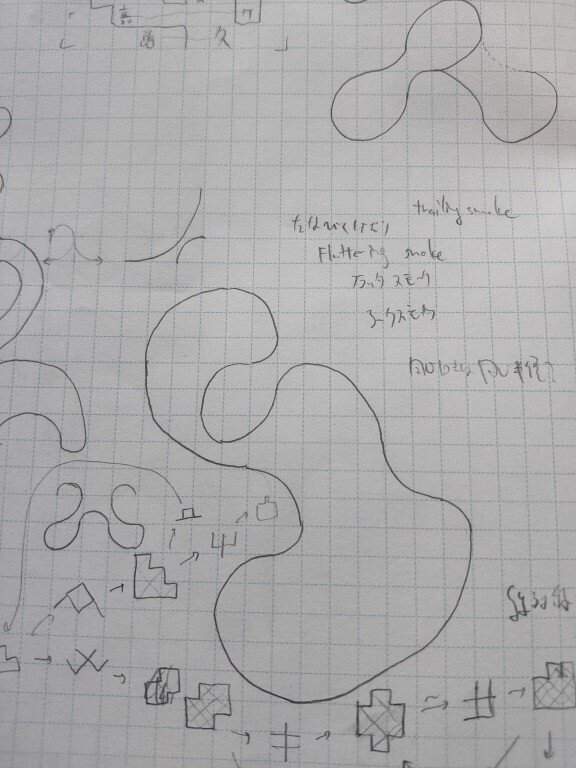
円弧

・半径0.5の半円
・半径1の四分円
の円弧を交互に組み合わせたループを作ろうとしていたものです。
どこかで間違えたのか、なかなかループが閉じず収拾がつかなくなりました。
偶奇がずれてるんだと思います。
変形盤面

↓のスパイラルヤジリンのイメージ図です。
スパイラルヤジリン
— うまや天国 (@ardjmk10Dqag) December 30, 2021
左右の同じアルファベットが書かれた辺同士は繋がっています(A〜I)。
太枠は特にどこかと繋がったりはしていません。https://t.co/eMVLJ6NLY6 pic.twitter.com/GNQhRA2ZDJ
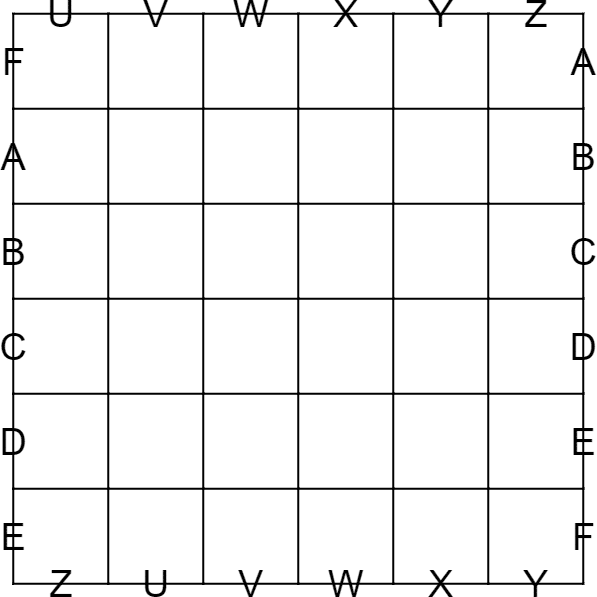
スパイラルヤジリンの盤面は円柱として実現できますが、もっとめちゃくちゃに外周を同一視した盤面を考えられます。
上の例は四隅の格子点近傍がめちゃくちゃになるものの、細かいことを気にしなければパズル上はどうにかなりそうです。
その他

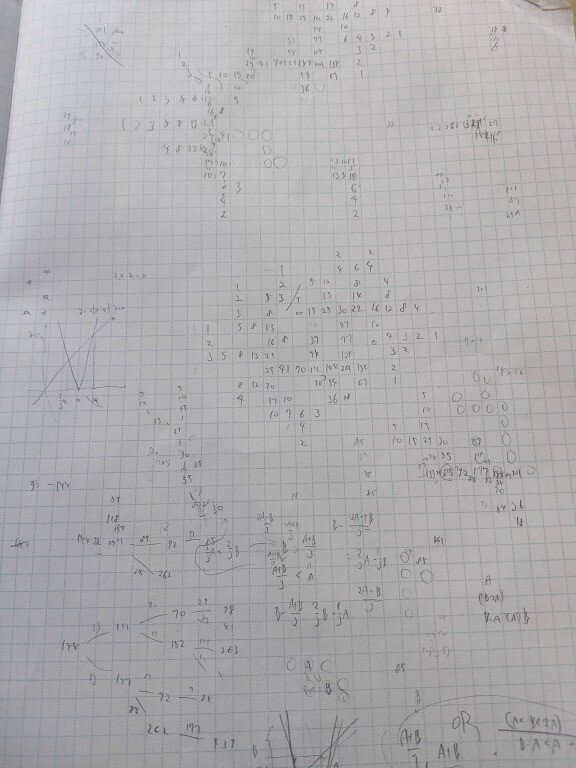


数字を入れ替えて部屋内の数字を連番にする
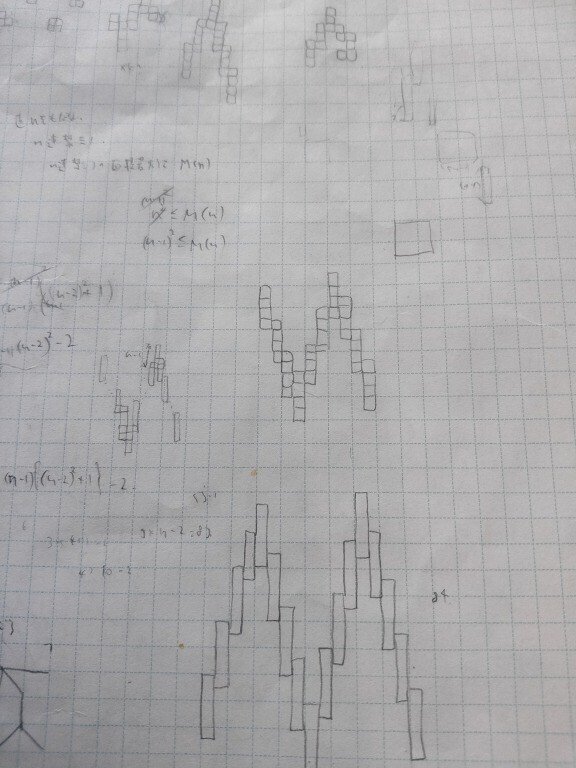
n^3ぐらいのオーダーで増大するものを構成した
非共円ポリオミノの拡張です。
(参考:にしなんとかさんの記事)「非共円ポリオミノについて」
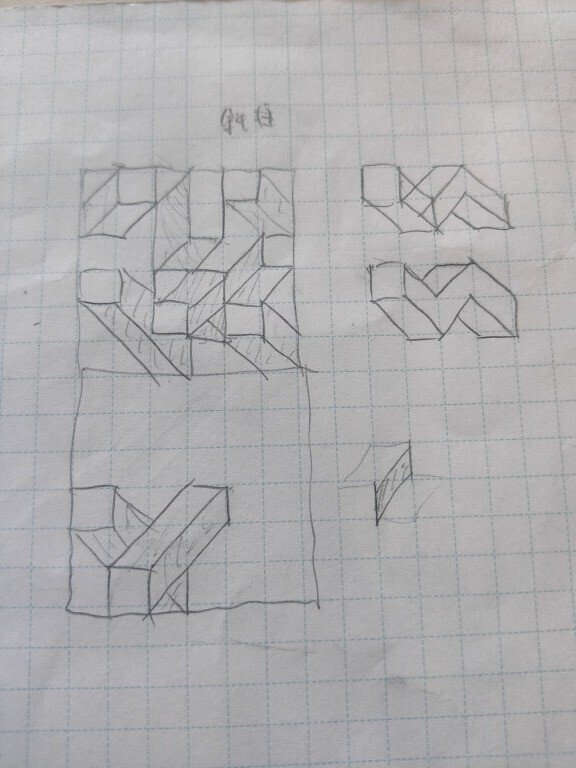

(bell, drop, leaf, fan)
用途はまだない
あとがき
今回アドベントの場をお借りしてパズルノートを振り返ってみました。
率直な感想としては、案外存在を忘れてたアイデアが見つかったりして普通に参考になりました。
あとはこのまま放置してたら永久に忘れてたなーというものもあり、せっかく思いついたアイデアは世に出さなもったいないと思いました。
皆さんも、本棚で眠っているパズルノートがあれば、見返してみると新たな発見があるかもしれませんよ。
この記事が気に入ったらサポートをしてみませんか?
