
振り子と円弧の気まぐれループ
こんばんは。うまや天国です。
今回はみんな大好きパリティの話をします。
といっても何か既存のループについて調べるというよりは、「振り子ループ」というものを考えたら色々見つかった(のと検索したら色々出てきた)ので、その性質とかをまとめます。
この記事を通し、ループは盤面の格子点上を通るとします。
1. 振り子ループ
ルール
次の性質を満たすループを振り子ループと呼ぶ。
①交差、枝分かれのないループ
②奇数長の辺は両端でU字に、偶数長の辺はS字に曲がる
そして、②の性質を振り子性と呼ぶことにします。

文章だけで見ると把握しづらいですが、上のように奇数長辺(緑)では両端でコの字で同じ方向に曲がり、偶数長辺(橙)ではSの字で異なる方向に曲がるということです。
端点の凹凸が奇数長辺だと一致、偶数長辺だと不一致ともいえます。
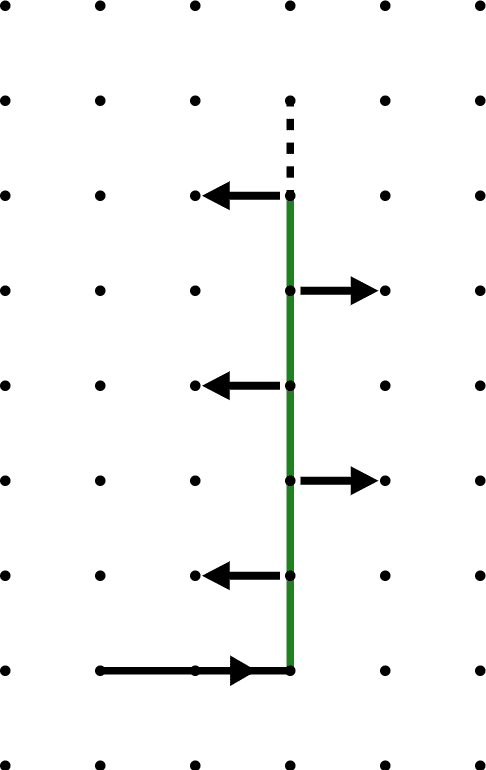
名前の由来は、左右曲がれる方向が振り子のように交互に入れ替わるからです。
周期2秒の振り子を持ちながら毎秒1マスのスピードで歩き、振り子の向いている方向にしか曲がれない、という風にも解釈できます。
動機
ループはマスの通り方によって何種類かに分類できます。
○タテヨコに通る
○タテヨコナナメに通る
・・・45°, 90°, 135°で曲がれる
・・・135°のみ曲がれる
○桂馬飛びで通る
○自由線で通る
これらのループの違いの内、解き味に与える要素として「各点における自由度」があると考えています。

タテヨコループの場合、線が次に進める方向は直進、左、右の3通りです。
一方、タテヨコナナメループなら、8方向から自身を除いた7通りの進み方があります。その意味で、ナナメ有りループの方が各点での選択肢が多く、解き味が重くなる傾向があるといえます。
この理論で行くと、各点での進み方が2通りぐらいだと考えることが少なく、良いパズルになる気がしてきませんか?
ということで直線部分の偶奇によって右左折を入れ替え、2通りにしたのが振り子ループというわけです。何も考えずに右左折の制限を入れるとループの向きに依存するので、S字とU字にしました。(かえって考えることが増えてしまったのはご愛嬌)
2. アークループ
ルール
互いに重ならない半径1の四分円の円弧からなる枝分かれ・交差のないループであって、線がなめらかにつながっているものをアークループと呼ぶ。

要するに同じサイズの1/4円弧を滑らかにつなげたやつです。
今回は円の中心が格子点上にあるものを考えます。
アークループの偶奇性
偶奇性を調べるにあたり、アークループが通り得る頂点や、各点での線の向きを考えます。
四分円弧は斜めの頂点同士をつなぐので、アークループは市松盤面で片方の色の頂点だけを通ります。
また、頂点における円弧の接線はそれぞれ縦と横になるため、縦・横にループが接する頂点は、下図のように交互に並びます。

ここで、ループに適当な向きを入れた時、白丸を通る線の向きを考えます。
ループは白丸と黒丸を交互に通るため、白丸から2つ円弧を通ると白丸に戻ります。

上図中央の白丸を下向きに線が通るとします。このとき、そこから2つの円弧で到達できる白丸は、ABCDの4つあります。
線の向きとしては、点A,Bは上向きに変化し、点C,Dは下向きのままです。言い換えると、真横にある白丸へ移動すると向きが変わるのに対し、斜めにある白丸へ移動しても向きは変わりません。
従って、線が上向きに通る白丸と下向きに通る白丸は、市松模様に交互に並びます。
同様の性質は黒丸についても成り立ちます。

以上をまとめると、上図のような左回りの円△と右回りの円▼が交互に並んだ盤面を考えた時、アークループはそれらの円弧をかいつまんでできたループと考えられます。
3. 振り子ループとアークループの関係
2つのループの同値性

アークループを構成する四分円弧について、それぞれ対応する弦に置き換えるとマスの対角線からなるループになります。
これを1/√2倍して斜めに倒すと、格子点をタテヨコに通るループが得られます。
実はこの操作により得られるループは、振り子ループの性質を満たします。
この意味で、振り子ループとアークループは同じものとみなせます。


この2つのループが一致するのは、振り子性から来る右左折のパターンと、円弧が滑らかになるための偶奇性が一致するからと解釈できます。
上の図でいえば、左折した直後の線は円弧が左回りになっているので"左折したがって"おり、なんとかうねうね直進するために右左折を交互に繰り返している・・・みたいなそんな感じだと思います。
振り子ループの流水モデル
アークループには偶奇性から、ループの向きを決めた瞬間に盤面の各辺を通れる向きが決まるほどの強い制約があることが分かっていました。
振り子ループはアークループと同値なため、同様の制約(盤面全体で線が通れる向きが決定)が期待できます。
そこで、ループの横線に着目します。

右向きの線が、ある点で上に曲がった後の動きを考えます。
このとき、縦方向に奇数マス進むと左に、偶数マス進むと右にのみ進めることが振り子性から従います。
従って、盤面の横列は、左にしか進めない行と右にしか進めない行が交互に並びます。
縦列でも同様なので、盤面で線が通れる向きは下図のようになります。

上図を斜めにして√2倍すると、「アークループの偶奇性」のラストの図と対応していることが分かります。
◇ループの矢印演算
いま、振り子ループに右回りの向きを考えます。
「線が上向きにしか通れない」ことが分かっている辺に隣り合う2マスを考え、A,Bとします。
そして、A,Bのループへの内側の入り方を考えます。

A,Bの内外として上図の①~④の4通りがあります。
このうち①④は内外が一致しているので、辺に線を引かなければ破綻しません。
一方、②③の場合は必ず線が引かれますが、ループは右回りとしているので、Aは外に、Bは中に入ります。
したがって、③だけがセーフで②は破綻します。
線の内側に入るマスをTrue、外側に出るマスをFalseとし、上記の結果を辺によるマスの二項演算と考えると、上向きの辺「↑」による式「A↑B」は、AならばB「A⇒B」と一致します。
つまり、「Aが内側ならばBも内側になる」という表出と同値になります。
この結果を踏まえ、先ほどの振り子ループが通れる盤面の向きを書き換えると下図になります。

「A>B」は「A⇒B」を表しています。
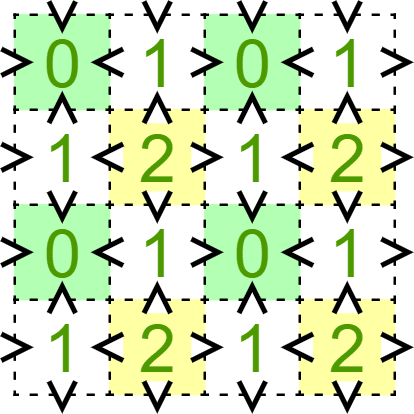
不等号に整合するよう数字を書き込むと上のようになります。不等号から、1のマスがループの内側に入ると、隣接する2つの0のマスも内側になります。また、2のマスが内側に入ると、周囲4マスも必ず内側になります。
したがって、「ループが振り子性を満たす」⇔「上の図において、ループの内側に入る全てのマスは、隣り合う外側のマスより数字が小さい」が成り立ちます(数字の入れ方はループの配置・向きの入れ方に依存します)。

この表現は、数字がマスの高さだとすると、あるマスに水を注いだ時、隣り合うマスで自分より低いところに流れ落ちる様子と似ています。そのためこの考え方を流水モデルと呼んでいます。
振る舞いのよくわからない交差なしループを、比較的とっつきやすい黒マス系パズルに帰着してくれる点が嬉しいですね。
Polystickによる分類
振り子ループはPolystick(Wikipedia)と対応付けることができます。
Polystickとはポリオミノの棒版みたいなやつで、↓の図を見ればなんとなく内容が分かるかと思います。

具体的には、ループの内側にある点のうち、流水モデル盤面で0のマスを頂点、1のマスを辺とみなすことでpolystickが得られます。

特に作り方から、1マスのループしか無いpolystickが対応し、
そのようなpolystickを"充填polystick"を呼ぶことにします。
逆に、全ての充填polystickに対して対応する振り子ループが存在するような気がしています。(ちゃんと示せたわけではないですがまあそうだろうと思います)


黒丸が頂点、白丸が最も近い2つの黒丸を結ぶ辺になる
これまでの結果をアークループに当てはめると、ループの内側にある点のうち、偶奇性から円弧の中心になりうる点(であってループの向きと同じ円の中心になるやつ)を頂点、中心にならない点を辺とみなすことでpolystickが得られます。このとき各辺は最も近い2黒点を結びます。
黒丸の説明は「アークループの偶奇性」のラストのやつです。
以上より、振り子ループ・アークループは充填polystickと同一視できることが分かります。
4. 逆振り子ループ
これまでの話で振り子ループは、アークループや充填polystickと実質的に同じであることが分かりました。
ただ、振り子性の定義にあった「奇数長辺がU字/偶数長辺がS字」という制約に必然性は無いので、偶奇を入れ替えたものも考えてみましょう。
ルール
次の性質を満たすループを逆振り子ループと呼ぶ。
①交差、枝分かれのないループ
②奇数長の辺は両端でS字に、偶数長の辺はU字に曲がる

逆振り子ループにおいては、奇数長辺の両端でカーブの凹凸が異なり、偶数長辺の両端で凹凸が一致します。
従って、ループの凹点・凸点になり得る点が盤面に交互にならびます。

アークループとの関係
逆振り子ループについても、振り子ループと同様にアークループと対応付けられます。

その方法として、図の上側のように辺からS字円弧への変換を考えます。
下側は振り子ループの辺→弦の対応を参考に置いています。
この方法だと振り子ループと異なり円弧の入れ方が2通りありますが、実質的には同じものです。

片方は比較的カーブが緩い"ゆるループ"に、もう片方はうねりが強い"うねりループ"になります。
ゆるループの方が見た感じ扱いやすそうなので、今回はこっちをメインに見てみましょう。
逆振り子性に対応するpolystick

逆振り子ループ→アークループの対応ができたので、これによりどのようなpolystickが対応するのか調べます。

例えば、ルール説明で出てきた逆振り子ループに対応するpolystickを考えると、いくつかの正方形が辺や点、線で引っ付いたものが出てきます。

シャカシャカみたいですね
アークループを取っ払うと、
◇polystickの頂点・・・逆振り子ループの凹点になり得る格子点のうち、ループの境界か内側にあるもの
◇polystickの辺・・・逆振り子ループの内側にあるマスの対角線で、黒丸を結ぶ方
に対応することが見て取れます。
(※凹点になっているのは今回ゆるループを採用しているためで、その"双対"であるうねりループだと凸点が頂点になります)
ここで、polystickの各頂点・マスの周りでどのような配置が破綻するかを調べると以下のようになります。

例えば辺条件の「1マスにちょうど3辺引くと破綻」は、下図で太点線のようにpolystickをおくと、凸点にしかならないはずの白丸が凹点になり破綻することによります。
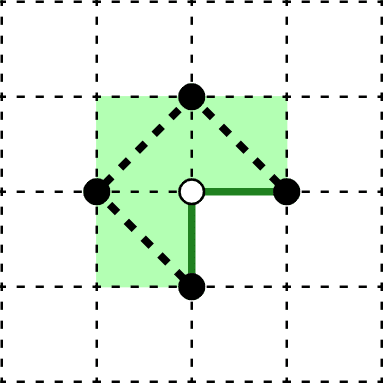
これらの頂点条件・辺条件を満たすpolystickを考えると、擬ポリオミノ同士が蛇腹線でつながった形になることが分かります(擬ポリオミノは斜め連結も許したポリオミノ)。
どことなくヤドリギみを感じます。

以上から逆振り子ループに対応するpolystickは、少なくとも上記の"ヤドリギミノ"の性質を満たすことが必要だと分かりました。
ただ、ヤドリギミノ全体が逆振り子ループに対応するか(何か他の必要条件が無いか)までは未確認です。
頂点条件と辺条件まで見たので大丈夫な気はしていますが、あくまで局所的な条件なので・・・
5. その他の性質・応用・展望
細かい性質
振り子ループ
・バッグの表出は奇数
・更にlohkousの表出は全て奇数
・面積は奇数
・外周の長さは4n
逆振り子ループ

・最小のと2番目に小さいのを考える限り面積・周長の偶奇無し
・擬ポリオミノとの関係から、シャカシャカで「斜め白四角は頂点連結」条件を付けた場合の黒三角による外周は逆振り子的・・・かと思ったら違いました。

パックマンみたいな塊を禁止しないと逆振り子的にならなかったです。
今後の応用・展望
○振り子ループに使った流水モデルで他のループも調べてみたいと思いました。
盤面全体でループの通る向きが決まっているときに使えそうです。
例えば全ての辺が1マスのループだと、0・1が交互に並んだ盤面になります。

○アークループへ対応づける時、振り子ループは弦を弧に、逆振り子ループは辺を斜め線に置き換えるような変換をしています。
逆に考えれば、振り子性・逆振り子性はその変換が無理なく行えるための条件とも捉えられます。
別の変換を考えれば新しい制約を持つループを作れそう。
○初めからループに向きを付け、辺長の偶奇で右左折を決めるバージョンも考えられます。
恐らくループが左回りか右回りかで丸っきり性質が変わりそうです。
○逆振り子ループの全貌は結局よく分かりませんでした。
1辺に対し2個の円弧をあてがっているせいで偶奇性が薄まったんじゃないかと予想してるんですが、かといって薄めずに済む言い換えも思いつかないので何か良い方法無いかなという感じです。
6. 先行研究
今回記事でいくつか用語を導入しましたが、実はアークループについては先行研究があります。
アークループはTangle、振り子ループ(と実質的に同じポリオミノ)はFleron polyominoという名前がついていました。Tangleという名称は、同名のおもちゃが元ネタが由来だそうです。
特に参考文献の[1]が今回の「アークループ~振り子ループ」の内容と非常に近しいです。
変な性質を持つループがどんどん見つかるといいですね。
参考文献
[1]
DOUGLAS A. TORRANCE "ENUMERATION OF PLANAR TANGLES"
https://arxiv.org/pdf/1906.01541.pdf
[2]
Erik D. Demaine, Martin L. Demaine, Adam Hesterberg, Quanquan Liu, Ron Taylor, and Ryuhei Uehara "Tangled Tangles"
[3]
Polyform Puzzles
https://puzzler.sourceforge.net/docs/polysticks-intro.html
この記事が気に入ったらサポートをしてみませんか?
