
Blenderのジオメトリーノードで懸垂線を作る。
はじめに
こんにちはとぅなです。今回がBlenderのジオメトリーノードで懸垂線を作成したのでnoteを書きました。
懸垂線とは、2点間を結ぶロープなどの垂れ下がるときに描く軌道のことで、ボールを投げた際の軌道である放物線のようなものであるという認識で問題ありません。
また、今回は今までのnoteと異なり7割方が数学の特に立式の話になり、同じことを画策する次の人の計算が楽になればという思いで書いています。
また、一般的な高校の数学では懸垂線の説明がされないと思いますが、なるべくわかるように説明していきます。
流れの確認
今回のnoteの流れをざっと説明します。
前半は、Blenderから離れて実際に作っていく中で考えたことを伝えながら計算します。
後半は、軽くノードの説明をします。
計算
以降の計算に用いたpdfデータを付属しておきます。必要があれば確認してください。
懸垂線とは
先ほど懸垂線が放物線のようなものだと伝えたと思いますが、この懸垂線も数式に落とし込むことができます。
これは、以下の双曲線関数というものが用いられます。
$${\displaystyle y = a\cosh\left(\frac{x}{a}\right)}$$
また、これは以下のように定義されます。
$${\displaystyle y =a\cosh\left(\frac{x}{a}\right) = \frac{a\left(e^{\frac{x}{a}}+e^{-\frac{x}{a}}\right)}{2}}$$
しかし、この式ではy軸対象のグラフしかできません。
そこで、今後は以下の一般式を与えて懸垂線を考えていきます。
後々説明しますが、双曲線関数は$${\sinh \cosh}$$があり、これは三角関数の性質に非常に似ています。
$${\sinh}$$の定義は以下の式になります。
$${\displaystyle \sinh(x) = \frac{e^{x}-e^{x}}{2}}$$
一般式
$${y=a\cosh\left(\frac{x-b}{a}\right)+c=\frac{a\left(e^{\frac{x-b}{a}}+e^{-\frac{x-b}{a}}\right)}{2}+c}$$
実装の際の想定
一度休憩を兼ねてBlenderに思いを馳せましょう。
ジオメトリーノードでどのようにこの線を作成することが一番効果的であるか考えます。
実用的なのは紐の端の2点の座標を与え、紐の長さを変化することができるようにする方法でしょう。
つまり、一般式でいうところのaに当たる部分は変数としてモディファイア―欄で操作できるようにし、b, cは2点の座標から自動的に決定できるようにすることが理想的です。
そこで次はb, cを導き出す式を計算で求めていきます。
計算
はじめに、紐の端である地点$${A_{1}, A_{2}}$$の座標を$${(x_{1}, y_{1}), (x_{2}, y_{2})}$$と置くと、
$${\displaystyle y_{1} = a\cosh\left(\frac{x_{1}-b}{a}\right)+c}$$
$${\displaystyle y_{2} = a\cosh\left(\frac{x_{2}-b}{a}\right)+c}$$
となります。これは同じ懸垂線であるため、b, cは同じものです。
まずはcを消します。
$${\displaystyle y_{1}-y_{2}-a\cosh\left(\frac{x_{1}-b}{a}\right)+a\cosh\left(\frac{x_{2}-b}{a}\right)=0}$$
式変形を行って、
$${\displaystyle \cosh\left(\frac{x_{1}-b}{a}\right)-\cosh\left(\frac{x_{2}-b}{a}\right)=\frac{y_{1}-y_{2}}{a}}$$
ここで、$${\displaystyle u=\frac{x_{1}-b}{a}, v=\frac{x_{2}-b}{a}}$$とします。
この際に左辺を以下のように式変形することができます。(計算は後述)
$${\displaystyle \cosh(u)-\cosh(v)=2\sinh\left(\frac{u+v}{2}\right)\sinh\left(\frac{u-v}{2}\right)}$$
よってuとvを元に戻して式変形をすると、
$${\displaystyle 2\sinh\left(\frac{\frac{1}{2}(x_{1}+x_{2})-b}{a}\right)\sinh\left(\frac{x_{1}-x_{2}}{2a}\right)=\frac{y_{1}-y_{2}}{a}}$$
$${\displaystyle \sinh\left(\frac{\frac{1}{2}(x_{1}+x_{2})-b}{a}\right)=\frac{y_{1}-y_{2}}{2a\sinh\left(\frac{x_{1}-x_{2}}{2a}\right)}}$$
sinhの逆関数を用いると(計算は後述)
$${\displaystyle \frac{\frac{1}{2}(x_{1}+x_{2})-b}{a}=\log\left(\frac{y_{1}-y_{2}}{2a\sinh\left(\frac{x_{1}-x_{2}}{2a}\right)}+\sqrt{\left(\frac{y_{1}-y_{2}}{2a\sinh\left(\frac{x_{1}-x_{2}}{2a}\right)}\right)^{2}+1}\right)}$$
よってbの値は、
$${\displaystyle b=\frac{x_{1}+x_{2}}{2}-a\log\left(\frac{y_{1}-y_{2}}{2a\sinh\left(\frac{x_{1}-x_{2}}{2a}\right)}+\sqrt{\left(\frac{y_{1}-y_{2}}{2a\sinh\left(\frac{x_{1}-x_{2}}{2a}\right)}\right)^{2}+1}\right)}$$
以上よりcの値は、$${A_{1}}$$の座標を用いると、
$${\displaystyle c = y_{1} - a\cosh\left(\frac{x_{1}-b}{a}\right)}$$
$${\displaystyle =y_{1}-a\cosh\left(\frac{x_{1}-\left(\frac{x_{1}+x_{2}}{2}-a\log\left(\frac{y_{1}-y_{2}}{2a\sinh\left(\frac{x_{1}-x_{2}}{2a}\right)}+\sqrt{\left(\frac{y_{1}-y_{2}}{2a\sinh\left(\frac{x_{1}-x_{2}}{2a}\right)}\right)^{2}+1}\right)\right)}{a}\right)}$$
これをBlenderの数式ノードを使って計算すれば理論上はできるというわけで、省略した計算を次に書いて計算フェーズは終了です。
オプション:省略した計算①
はじめの計算式は、以下のようなものでした。これを証明していきます。
$${\displaystyle \cosh(u)-\cosh(v)=2\sinh\left(\frac{u+v}{2}\right)\sinh\left(\frac{u-v}{2}\right)}$$
(左辺)
$${=\cosh(u)-\cosh(v)}$$
$${\displaystyle =\frac{e^{u}+e^{-u}}{2}-\frac{e^{v}+e^{-v}}{2}}$$
$${\displaystyle = \frac{e^{u}-e^{v}+e^{-u}-e^{-v}}{2}}$$
$${\displaystyle = \frac{1}{2}\left(e^{\frac{u+v}{2}}e^{\frac{u-v}{2}}-e^{\frac{u+v}{2}}e^{-\frac{u-v}{2}}-e^{-\frac{u+v}{2}}e^{\frac{u-v}{2}}+e^{-\frac{u+v}{2}}e^{-\frac{u-v}{2}}\right)}$$
$${\displaystyle = 2\cdot \frac{\left(e^{\frac{u+v}{2}}-e^{-\frac{u+v}{2}}\right)\left(e^{\frac{u-v}{2}}-e^{-\frac{u-v}{2}}\right)}{4}}$$
$${\displaystyle = 2\sinh\left(\frac{u + v}{2}\right)\sinh\left(\frac{u - v}{2}\right)}$$
=(右辺)
こんな感じになります。
オプション:省略した計算②
$${\sinh}$$の逆関数を導出します。
$${\displaystyle \sinh(x) = \frac{e^{x}-e^{-x}}{2}}$$
より、
$${\displaystyle y = \frac{e^{x}-e^{-x}}{2}}$$
をxについて解きます。
$${\displaystyle e^{x} + 2y = e^{-x}}$$
$${\displaystyle e^{2x} + 2ye^{x} - 1=0}$$
解の公式を用いて$${e^{x}}$$について解くと、
$${\displaystyle e^{x} = y \pm \sqrt{y^{2}+1}}$$
$${\displaystyle x = \log\left(-y \pm \sqrt{y^{2}+1}\right)}$$
よって逆関数は
$${\displaystyle y = \log\left(-x \pm \sqrt{x^{2}+1}\right)}$$
です。
Blenderに落とし込む
ここまで計算できればBlenderにあとはこれを実装するだけになります。
始点と終点を指定する。
まずは始点と終点の座標を与える必要があります。
ぱっと思いつく限りいくつか方法はありますが、2つだけ紹介します。
モディファイア―の入力欄で座標を指定する方式
エンプティを2つ配置し、それらの座標を取得する方式
今回は2つ目を採用しました。これは、座標を入力して望みの場所に置くよりもビューポート上で2点を配置する方が実用的だと判断したためです。
座標の取得方法は下図のようにすればいいです。


続いてこれらを結ぶカーブラインを作成し、任意の値で分割していきます。
この分割したひとつひとつの頂点を計算で求めた座標に配置することで懸垂線を作ります。つまりここでこの分割の値を多くすれば滑らかなで正確な懸垂線に近似できるというわけです。
そのためのノードは以下のようになります。

ここで、位置設定ノードの位置に計算した座標を入れることになります。
任意の懸垂線の導出
ここまで来て、先ほどまで立式していたものは2次元の話で、今回は3次元の値になるため複雑になるのではと考えた人もいるかもしれません。
しかし、難しく考える必要はありません。
懸垂線の場合、座標が分布するのは同一平面になるのが想像できると思います。
そこで、先ほどの立式におけるy軸をBlender上のz軸で見立て、x軸を始点と終点のベクトルのx,y成分を抽出したもので見立てます。
必ずしも直交座標がx,y,z座標系である必要がないというのはgeonodeで使うことが多いかもしれません。
また、この場合どこを原点としても問題ないため、片方の点を原点としてしまいます。
そうすると、先ほどの式が$${(x_{1}, y_{1}) = (0, 0)}$$となるため、BとCの計算が楽になります。
準備のためのノードは以下のようになります。

2つの位置ベクトルを減算しベクトルを出し、x,y成分を抽出し、長さノードをつなげることで、$${x_{2}}$$の値を導出。z成分は直接$${y_{2}}$$の値となり、Aは任意の値を取るためグループ入力ノードから持ってきます。
懸垂線の計算
ここまでくればあとは少しになります。求めたABCを使って懸垂線の式に代入します。注意すべきなのは分割したカーブの座標を取る方法で、今回は、範囲マッピングを用いて以下のようにしています。
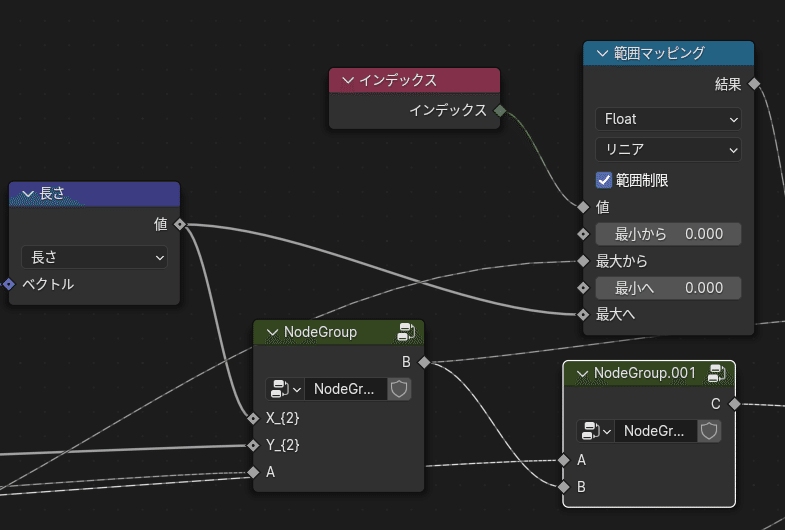
この範囲マッピングの結果の値は$${\displaystyle y = a\cosh\left(\frac{x-b}{a}\right)+c}$$のxに代入されます。
次に計算後のyの扱いを見て最後になります。

先ほど出た位置設定ノードの位置に挿す座標の内zに当たる部分が計算後のyの値になります。
以上でノードの解説は終了になります。
運用方法
最後に、geonodeでは、カーブオブジェクトを生成しても直接カーブとしてモディファイア―を適用できないという問題があります。そのため、適宜メッシュ化を行い、モディファイアの適用後に再度カーブ化を行う必要があることだけ注意してください。
最後に
いままでと異なり数学の側面が強いnoteを書かせていただきました。厳密な計算の扱いは少し間違いがある可能性があります。そこだけ注意してください。
今回計算の確認のためにつかったpdfデータがあるため、一応配布しておきます。立式パートが丸々これの解説となっているため、補助として使うことができるかもしれません。
もし、わからないことがございましたら、コメントかTwitter(現X)にてコンタクトを取ってください。
以上とぅなでした。
この記事が気に入ったらサポートをしてみませんか?
