世界の法則を知るために－微分・積分とは？⑱積分の計算方法(7)

前回は、定積分が面積になることの紹介と、具体例を使った確認をしました。
また具体例を他の方法で解き、
$${\displaystyle S=\int_a^b{y}dx}$$
のような定積分は$${ x}$$の範囲が、
　 $${ 0}$$から上端までの面積$${ -}$$$${ 0}$$から下端までの面積
という計算をしていることを書きました。
今回は、定積分が面積になることの証明をします。
この証明は難しい内容となりますが、読んでみてください。
以下では上端を$${ b}$$、下端を$${ a}$$とすると、$${ 0 \leqq a \leqq b,y \geqq 0}$$
のときとします。

定積分が面積になる理由の証明

次の、
$${ \displaystyle \int_a^b{ydx}}$$
のような定積分は、$${ x}$$が$${ a}$$から$${ b}$$までの範囲の面積となることの証明をします。
以下では、証明に使う文字や記号、具体的に示す式、この式の証明について書いていきます。

準備

証明に使う文字や記号について書きます。
証明では、
$${ y}$$を$${ x}$$で不定積分する
と、
$${ \displaystyle \int{ydx}=Y+C}$$
となるとします。
このとき定積分は、
$${ \displaystyle \int_a^b{ydx}=\left[ Y \right]_a^b}$$
となります。
ここで$${ Y}$$という式の$${ x}$$に、上端である$${ b}$$を代入した式を$${ Y_b}$$、下端である$${ a}$$を代入した式を$${ Y_a}$$とすると、
$${ \displaystyle \left[ Y \right]_a^b=Y_b-Y_a}$$
となります。
これらから、
$${ \displaystyle \int_a^b{ydx}=Y_b-Y_a}$$
となります。

方針

今回は、
$${ \displaystyle S=\int{ydx}=Y+C}$$
となることを証明します。
ここで$${ S}$$は、$${ x}$$が$${ 0}$$から$${ x}$$までの範囲の面積としています。
もしこれがわかると、
$${ \displaystyle \int_a^b{ydx}}$$
は、$${ x}$$が$${ a}$$から$${ b}$$までの範囲の面積となることがわかります。
これは、
$${ \displaystyle S=\int{ydx}=Y+C}$$
は、$${ x}$$が$${ 0}$$から$${ x}$$までの範囲の面積としているため、この式の$${ x}$$に下端である$${ a}$$を代入した、
$${ Y_a+C}$$
は、$${ x}$$が$${ 0}$$から$${ a}$$までの範囲の面積となり、これを$${ S_a}$$とします。
同じように、この式の$${ x}$$に上端である$${ b}$$を代入した、
$${ Y_b+C}$$
は、$${ x}$$が$${ 0}$$から$${ b}$$までの範囲の面積となり、これを$${ S_b}$$とします。
このとき、$${ x}$$が$${ a}$$から$${ b}$$までの範囲の面積は、
　 $${ 0}$$から上端までの面積$${ -}$$$${ 0}$$から下端までの面積
となることを使い、
　 $${ 0}$$から$${ b}$$までの面積$${ -}$$$${ 0}$$から$${ a}$$までの面積
となるので、
$${ S_b-S_a}$$
となります。
これらから、
$${ S_b-S_a=(Y_b+C)-(Y_a+C)=Y_b-Y_a}$$
となります。
また定積分は、
$${ \displaystyle \int_a^b{ydx}=Y_b-Y_a}$$
となるので、
$${ \displaystyle S_b-S_a=Y_b-Y_a= \int_a^b{ydx}}$$
となります。
このことから、
$${ \displaystyle \int_a^b{ydx}=S_b-S_a}$$
となるので、
$${ \displaystyle \int_a^b{ydx}}$$
は、$${ x}$$が$${ a}$$から$${ b}$$までの範囲の面積となります。
これらから、
$${ \displaystyle S=\int{ydx}=Y+C}$$
となることがわかれば良いとなるので、
$${ \displaystyle S=Y+C}$$
の証明をします。

証明

次の、

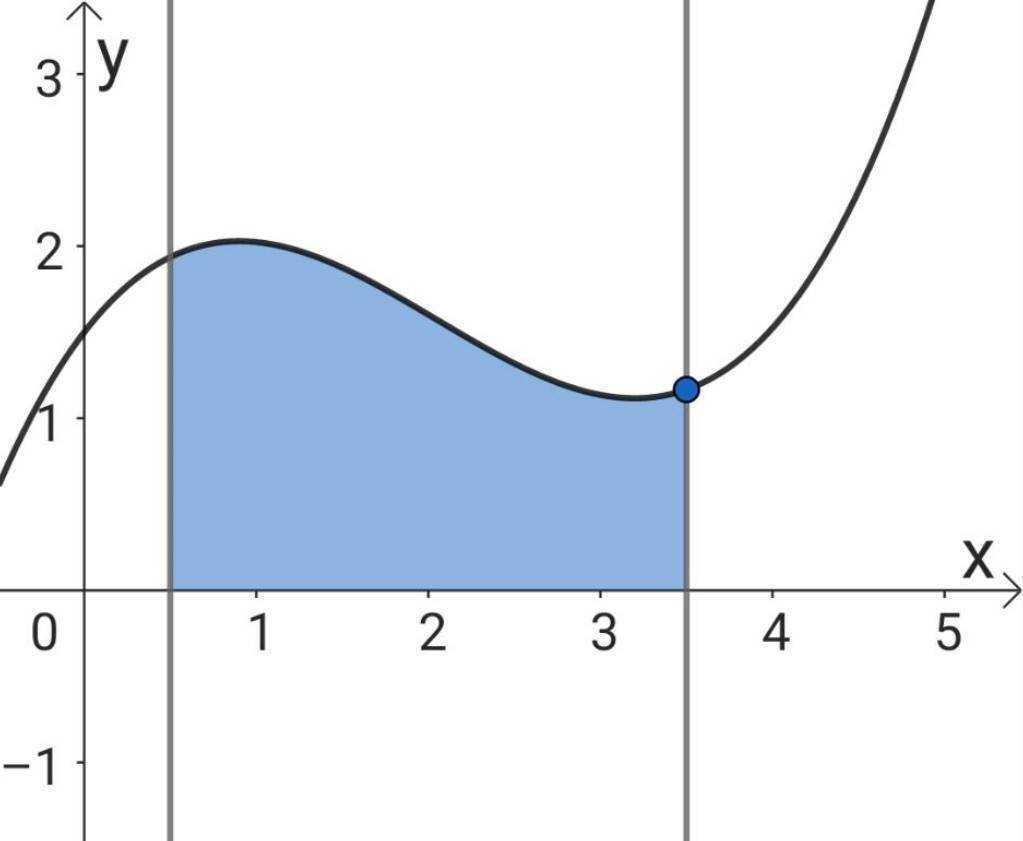
の黒線の関数を$${ y}$$、青点の座標を$${ (x,y)}$$、青色部分の面積を$${ S}$$とします。
この$${ S}$$は、$${ x}$$が$${ 0}$$から$${ x}$$までの範囲の面積としています。
このとき、
$${ \displaystyle S=Y+C}$$
となることを証明します。
このグラフで、

のように、青点が黒線上を動き赤点の場所まで動いた場合を考えます。
このとき、$${ x}$$方向に$${ \Delta x}$$動いたとし、赤色部分は増えた分の面積で$${ \Delta S}$$とします。
この$${\Delta x }$$となる部分を、横幅と呼びます。
ここで、

のように、赤色部分の面積を取り出して考えてみましょう。
また、

のような青い長方形を考えます。
この青い長方形の面積は、青点の座標を$${ (x,y)}$$、青い長方形の横の長さは横幅となるので、
$${ y×\Delta x}$$
となります。
ここで赤点を、黒線上を動かし青点に近づけていくと、

のようになります。
このグラフから横幅が小さくなり、赤色部分の面積と青い長方形の面積はほぼ同じとなり、
$${ \Delta S \fallingdotseq y×\Delta x}$$
となります。
このとき同じではないので、ほぼ同じことを表す記号である$${\fallingdotseq}$$を使っています。
この式の両辺を$${ \Delta x}$$で割ると、
$${\dfrac{ \Delta S}{\Delta x} \fallingdotseq y}$$
となります。
ここでさらに赤点を近づけ、さらに横幅を小さくすると、

のように、赤色部分の面積と青い長方形の面積はさらに同じとなっていきます。
このため、横幅である$${ \Delta x}$$を、
$${ 0}$$に限りなく近づけたとき
を考えると、赤色部分の面積と青い長方形の面積は同じとなります。
このことから、
$${\dfrac{ \Delta S}{\Delta x} \fallingdotseq y}$$
は、ほぼ同じという意味の$${ \fallingdotseq }$$ではなく、同じという意味の$${ =}$$となります。
また、$${ \Delta }$$を$${ d}$$と置き換えることができます。
これらから、
$${\dfrac{ \Delta S}{\Delta x} \fallingdotseq y}$$
は、
$${\dfrac{ d S}{d x} = y}$$
となります。
この式から、
$${ S}$$を$${ x}$$で微分すると$${ y}$$となる
となります。
このとき逆の計算を考えると、
$${ y}$$を$${ x}$$で不定積分すると$${ S}$$となる
と言えます。
このことから、
$${ \displaystyle S=\int{ydx}}$$
となります。
ここで、
$${ \displaystyle \int{ydx}=Y+C}$$
としているので、
$${ \displaystyle S=Y+C}$$
となります。

まとめ

今回は、定積分が面積になることの証明をしました。
この証明は、
$${ \displaystyle S=\int{ydx}=Y+C}$$
となることから、
$${ \displaystyle \int_a^b{ydx}}$$
が、$${ x}$$が$${ a}$$から$${ b}$$までの範囲の面積となることがわかります。
この証明は難しい内容なので、全てを理解できなくても良いと思います。
たしかに、なりそうだなと思えただけでも十分だと思います。
また、数学的には厳密には不十分なところはあるかもしれません。
しかし、面積と積分のつながりを理解はできるかと思います。
今回は、できるだけ簡単な数学でつながりを理解することを目的としているので、許していただければと思います。

今回で、微分・積分の計算方法は終わりとなります。
次回からは応用編として、微分・積分がどのように使われているのか、より具体的に書いていきます。