世界の法則を知るために－微分・積分とは？微分の応用例(1)

微分では微小変化、積分ではいろいろな面積を求められます。
しかし具体的に何に使えるのか等、よくわからないと思います。
このため、微分・積分の応用例について書いていきます。
今回は、微分の応用例について書きます。
ある関数を微分したものは微小変化となるだけではなく、重要なものである接線の傾きでもあります。
今回はなぜ接線の傾きとなるのか、この接線の傾きがなぜ重要なものかについて書いていきます。
具体的に、
$${ y=-2x^2+8x-3}$$
のグラフを書くことができることを最終目標とします。

なぜなるのか

なぜ接線の傾きとなるのかの解説のため、まずは接線とは何かと微分の考え方の復習をします。
次にこれらを使って、なぜ接線の傾きになるのかの理由について書きます。

復習

接線とは何かの復習のため、

の黒線のグラフ、グラフ上の青点を考えます。
この青点の接線は、

の青線となります。
この青線のように接線とは、黒線のある１つの点でのみ重なるような直線のことです。
また、この青点のように黒線と青線が重なっている点を接点と言います。
次に微分の考え方の復習のため、

のように、青点が黒線上を動き赤点の場所まで動いた場合を考えます。
ここで青点を動かすとき、必ず黒線上を動くとします。
また２本の赤い点線間の距離を横幅、２本の青い点線間の距離を縦幅とし、それぞれ$${ \Delta x,\Delta y}$$とします。
微分を考えるとき、赤点を青点にどんどん近づけていき横幅を、
ゼロに限りなく近づけたとき
とします。
また微分は変化の割合、
$${ \dfrac{\Delta y}{\Delta x}}$$
の横幅である$${ \Delta x}$$を、
ゼロに限りなく近づけたとき
の計算をします。

理由

微分の考え方を使い、接線の傾きを求めてみましょう。
接線の傾きを求めるため、微分の考え方と同じように考えます。
ただし、

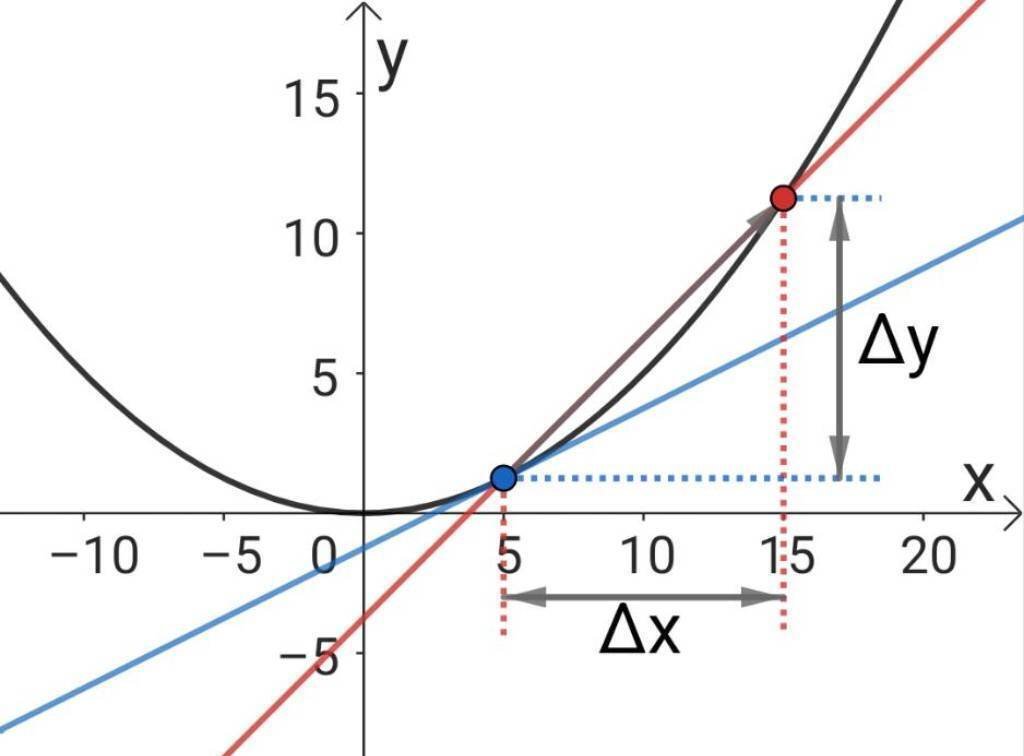
の赤線である青点と赤点を通る直線、青線である青点を接点とする接線を書いた状態で考えます。
このとき、赤点を青点にどんどん近づけていくと、

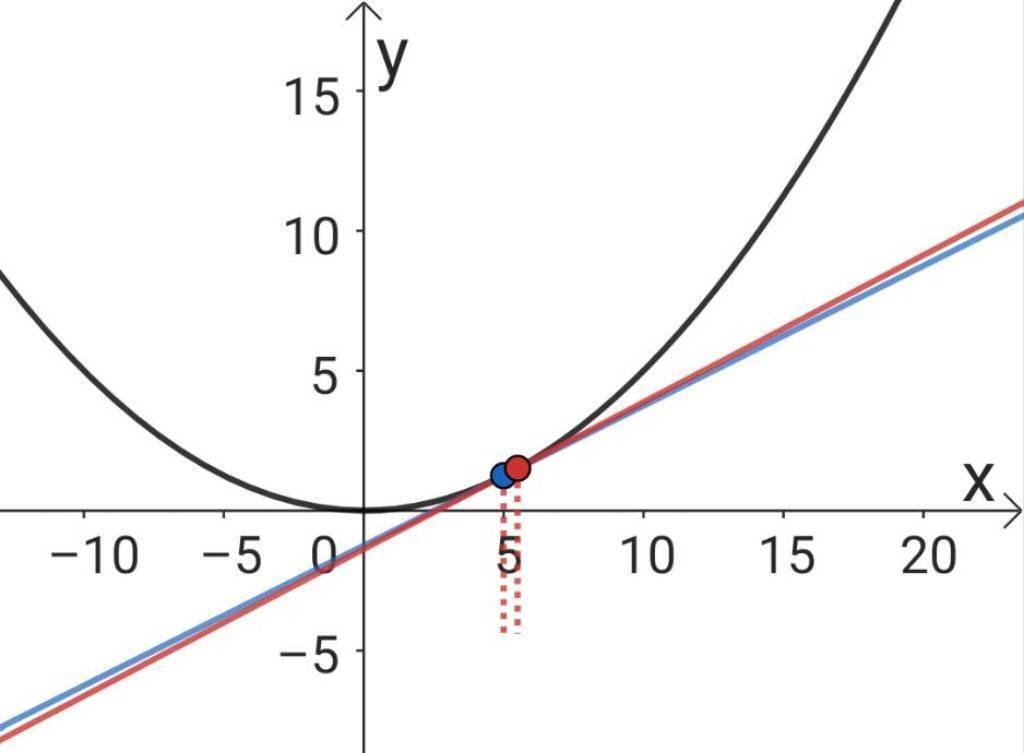
のようになります。
この場合の赤線は、青線である接線とほぼ同じになります。
ここで横幅である$${ \Delta x}$$を、
ゼロに限りなく近づけたとき
を考えると、赤線と青線である接線は同じとなります。
また赤線の変化の割合、
$${ \dfrac{\Delta y}{\Delta x}}$$
は赤線の傾きとなります。
このとき横幅である$${ \Delta x}$$を、
ゼロに限りなく近づけたとき
である、
$${ \dfrac{d y}{d x}}$$
を考えてみましょう。
この場合、赤線と青線である接線は同じとなるので、
$${ \dfrac{d y}{d x}}$$
は青線である接線の傾きとなります。
つまりある関数を微分にしたものは、ある関数の接線の傾きとなります。
正確には、
$${ \dfrac{d y}{d x}}$$
は、ある$${ x}$$のときのある関数$${ y}$$の接線の傾きとなります。

なぜ重要か

ある関数$${ y}$$を微分したものである、
$${ \dfrac{d y}{d x}}$$
は、ある$${ x}$$のときの$${ y}$$の接線の傾きとなります。
このある$${ x}$$のときの$${ y}$$の接線の傾きがわかると、どのような形のグラフになるかわからないような、複雑な形のグラフを書くことができます。
このことの解説のため、あるグラフ上にある青点の右側を考えてみましょう。
このとき、

のように、青点の右上に赤点があり、青点と赤点の間は黒線のようになったとします。
つまり、青点から$${ x}$$が増えたとき、$${ y}$$が増えた場合を考えます。
この場合、青点と赤点の間の黒点を接点とする接線を書くと、

の青線のようになります。
このとき接線は右上がりとなるので、接線の傾きはプラスとなります。
これらから、ある点から$${ x}$$が増えたとき、$${ y}$$が増えた場合、接線の傾きはプラスとなります。
同じように考えると次の、

のように、青点の右下に赤点があり、青点と赤点の間は黒線のようになったとし、青点と赤点の間の黒点を接点とする接線を書くと、

のようになり、接線は右下がりとなるので、接線の傾きはマイナスとなります。
これらから、ある点から$${ x}$$が増えたとき、$${ y}$$が減った場合、接線の傾きはマイナスとなります。
ここで、接線の傾きがゼロとなる場合を考えてみましょう。
接線は直線なので、
$${ y=ax+b}$$
のような一次関数となります。
接線の傾きがゼロとなる場合は、一次関数の傾きは$${ a}$$なので、
$${ a=0}$$
となり、
$${ y=ax+b=0×x+b=b}$$
となります。
この式のグラフを書くと、$${ x}$$軸に平行となる真横の直線となります。
接線が真横の直線となるところではどのようになるか、

のような黒線のグラフを使って考えてみましょう。
このグラフに真横の直線となる接線を書くと、

の青線のようになり、接点は赤点と黒点のようになります。
この赤点の付近で$${ x}$$が増えたとき、$${ y}$$は赤点の左側は減っていて右側は増えています。
同じように黒点の付近で$${ x}$$が増えたとき、$${ y}$$は黒点の左側は増えていて右側は減っています。
つまり赤点と黒点は、$${ y}$$の増減の境目となっています。
このように接線の傾きがゼロになる場合、接点は境目となります。
これらをまとめると、$${ x}$$が増えたとき、

• $${ y}$$が増えている場合、接線の傾きである$${ \dfrac{d y}{d x}}$$がプラスとなり、接線は右上がりになる

• $${ y}$$が境目の場合、接線の傾きである$${ \dfrac{d y}{d x}}$$がゼロとなり、接線は真横になる

• $${ y}$$が減っている場合、接線の傾きである$${ \dfrac{d y}{d x}}$$がマイナスとなり、接線は右下がりになる

となります。
これらから接線の傾き、
$${ \dfrac{d y}{d x}}$$
がプラス、ゼロ、マイナスのどの場合となるかの$${ x}$$の値を調べると$${ y}$$の増減がわかり、複雑な形のグラフを書くことができます。

まとめ

今回は、ある関数$${ y}$$を微分したものである、
$${ \dfrac{d y}{d x}}$$
は、接線の傾きとなること、微分の考え方や変化の割合から接線の傾きとなることについて書きました。
また接線の傾き、
$${ \dfrac{d y}{d x}}$$
がプラス、ゼロ、マイナスのどの場合となるかの$${ x}$$の値を調べると$${ y}$$の増減がわかり、複雑な形のグラフを書くことができることについて書きました。
数学では特に、複雑な形のグラフを書くときに、微分がよく使われます。
次回は今回の内容を使って、最終目標としていた、
$${ y=-2x^2+8x-3}$$
のグラフを書きます。