世界の法則を知るために－微分・積分とは？積分の応用例(3)

ある関数$${ y}$$と$${ x}$$軸で囲まれた部分の、$${ x}$$が$${ a}$$から$${ b}$$までの範囲を、$${ x}$$軸のまわりに一回転させた回転体の体積を$${ V}$$とすると、
$${\displaystyle V=\int_a^b{\pi y^2 dx}}$$
となります。
今回はこの式を使って、最終目標の１つである球の体積の公式を求めます。
球の体積の公式は中１で習いますが、公式を覚えるだけでなぜ公式のようになるかはわからないと思います。
今回の内容がわかれば、球の体積がなぜ公式のようになるかわかります。

球の体積

次の、

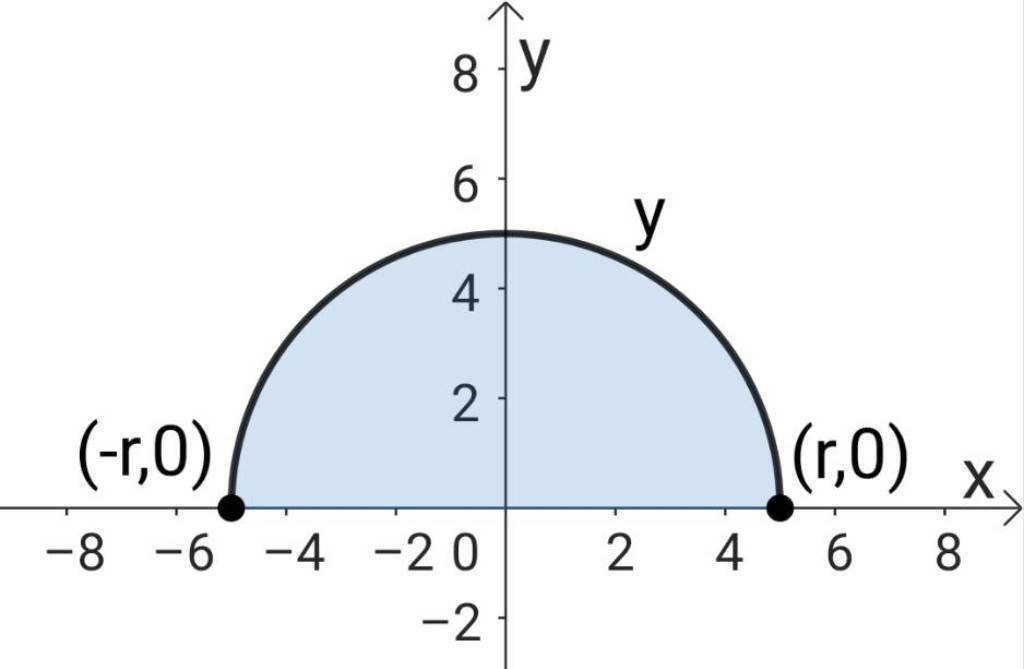
の黒線のような半円を表しているある関数$${ y}$$、青色部分のようなある関数$${ y}$$と$${ x}$$軸で囲まれた部分の、$${ x}$$が$${ -r}$$から$${ r}$$までの範囲を、$${ x}$$軸のまわりに一回転させた回転体の体積を$${ V}$$とすると、
$${ \displaystyle V=\int_{-r}^r{\pi y^2 d x}}$$
となります。
このとき、回転体は半径が$${ r}$$の球となります。
この式で、$${ x}$$の範囲を$${ -r}$$から$${ r}$$までとしたので、上端と下端が変わっていることに注意しましょう。
また、半径が$${ r}$$の球の体積は公式を使うと、
$${ \displaystyle \dfrac{4}{3}\pi r^3}$$
となります。
ここでは、定積分を使った回転体の体積の求め方を使って、球の体積の公式を求めてみましょう。
ここで、球の体積を計算するために、半円を$${ x,y}$$で表した式が必要になります。
まず半円を$${ x,y}$$で表した式がどのようになるか解説し、この式と定積分を使った回転体の体積の求め方を使って、球の体積の公式を求めます。
以下では、この半円を$${ x,y}$$で表した式を半円の式と言い、半径が$${ r}$$の球を考えます。

半円の式

半円の式を$${ x,y}$$を使って表すには、三平方の定理を使うため、三平方の定理の紹介をします。
次の、

のような直角三角形を考えてみましょう。
この直角三角形の辺の長さには、
$${ a^2+b^2=c^2}$$
という関係があります。
これを三平方の定理と言います。
この三平方の定理を使うと、$${ x,y}$$を使って半円の式を表すことができます。
次の、

のような半径$${ r}$$、中心$${ O(0,0)}$$の半円を考えてみましょう。
この半円上に、

という点$${ A(x,y)}$$を考えます。
このとき、

のように、三角形$${ AOB}$$が直角三角形になるようにします。
この直角三角形$${ AOB}$$の辺の長さは、
$${OB=x,AB=y,OA=r}$$
となります。
これらの辺の長さは三平方の定理より、
$${ x^2+y^2=r^2}$$
となり、この式が半円の式となります。

体積

球の体積を$${ V}$$とすると、定積分を使った回転体の体積の求め方から、
$${\displaystyle V= \int_{-r}^{r}{\pi y^2 dx}}$$
となり半円の式は、
$${ x^2+y^2=r^2}$$
となります。
これらから球の体積の公式を求めてみましょう。
半円の式、
$${ x^2+y^2=r^2}$$
より、
$${ y^2=r^2-x^2}$$
となります。
これを、
$${\displaystyle V= \int_{-r}^{r}{\pi y^2 dx}}$$
に代入すると、
$${\displaystyle V= \int_{-r}^{r}{\pi (r^2-x^2) dx}=\int_{-r}^{r}{(\pi r^2-\pi x^2) dx}}$$
となります。
この式を、$${ \pi,r}$$は定数であることに注意して計算すると、
$${\displaystyle V=\left[ \pi r^2 x-\dfrac{\pi}{3} x^3 \right]_{-r}^{r}}$$
  $${\displaystyle =\left( \pi r^2 r-\dfrac{\pi}{3} r^3 \right)-\left\{ \pi r^2 (-r)-\dfrac{\pi}{3} (-r)^3 \right\}}$$
　$${\displaystyle =\pi r^3 -\dfrac{\pi}{3} r^3  +\pi r^3 -\dfrac{\pi}{3} r^3}$$
　$${\displaystyle =\dfrac{4}{3}\pi r^3}$$
となります。
この結果は公式を使った結果、
$${\displaystyle \dfrac{4}{3}\pi r^3}$$
と同じになります。
このようにして、球の体積の公式を求めることができます。

まとめ

今回は、ある関数$${ y}$$と$${ x}$$軸で囲まれた部分の、$${ x}$$が$${ a}$$から$${ b}$$までの範囲を、$${ x}$$軸のまわりに一回転させた回転体の体積を$${ V}$$とすると、
$${\displaystyle V=\int_a^b{\pi y^2 dx}}$$
となることを使って球の体積の公式、
$${ \displaystyle \dfrac{4}{3}\pi r^3}$$
を求めました。
特に球の体積の公式は、中１で習うときに公式を覚えるだけで、なぜ公式のようになるかはわからないと思います。
しかし、今回のように定積分を使った回転体の体積の求め方がわかれば、球の体積が公式のようになることがわかります。
次回は、球の表面積の公式を求めます。
微分を使うと、球の表面積の公式を求めることができます。