世界の法則を知るために－微分・積分とは？－⑦微分の計算方法(2)

微分の計算方法を理解するためには、変化の割合を理解する必要があります。
この変化の割合は、増加量から求められます。
また、この微分の計算ではギリシャ文字である$${ \Delta}$$がよく使われます。
これらから今回は変化の割合、増加量、デルタについて解説します。
以下では、前回と同じようにグラフを使います。
ここでも前回と同じように横軸を$${ x}$$、縦軸を$${ y}$$とします。
また横方向を$${ x}$$方向、縦方向を$${ y}$$方向と言います。

今回の内容も、すでに理解している場合は読み飛ばして良いと思います。
目次を参考に、各自わからない場合は読んでいただければと思います。

デルタ

微分では、よくデルタを使います。
これはギリシャ文字で、$${ \Delta}$$と書きます。
このデルタは、数学で差を表すためによく使われます。
よく使われる例として、

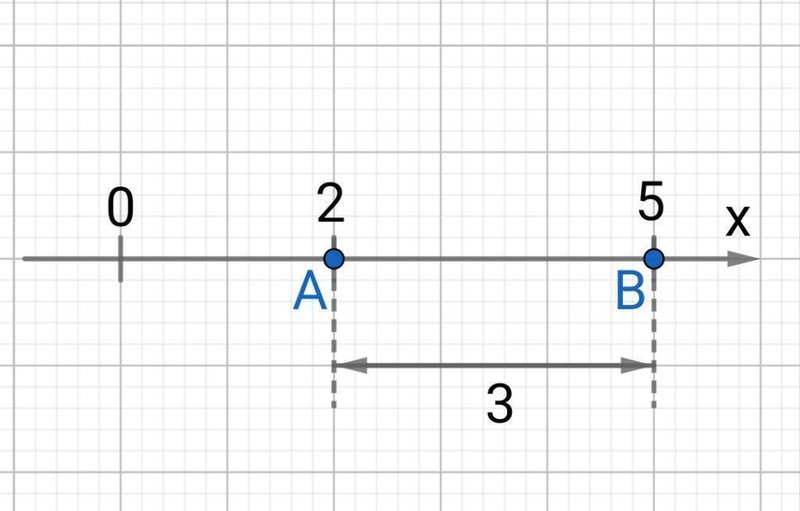
のような、数直線上にある２つの点$${ A,B}$$を考えます。
ここで、この数直線は$${ x}$$軸とします。
また$${ B}$$は、$${ A}$$から右に$${ 3}$$動いた点とします。
この$${ AB}$$間の距離は、
$${ 5-2=3}$$
のように、引き算を使って求められます。
これらから、デルタは数学で差を表すためによく使われ、距離は引き算により求められるので、
$${ \Delta x=5-2=3}$$
のように、距離に対してよくデルタを使って表現します。
ここで、$${ x}$$方向の距離を表しているため、$${ \Delta}$$の後に$${ x}$$を使い、$${ \Delta x}$$としています。
このとき$${ \Delta x}$$は、
$${ \Delta \times x}$$
という意味ではなく、$${ \Delta}$$と$${ x}$$の２文字で１組となります。
特に、ある方向にある距離だけ動かすような場合にデルタを使います。
同じように考えると、$${ y}$$方向の距離を表すためには、$${ \Delta y}$$となります。

今まで横幅、縦幅という表現を使っていました。
この横幅は$${ x}$$方向の距離、縦幅は$${ y}$$方向の距離と同じになります。
この後で基本的に横幅を$${ \Delta x}$$、縦幅を$${ \Delta y}$$と表現しています。

変化の割合と増加量

ここでは微分の計算に必要な、変化の割合について解説します。
変化の割合は、増加量を使って求めます。
これらから増加量、変化の割合の解説をします。

増加量

次の、

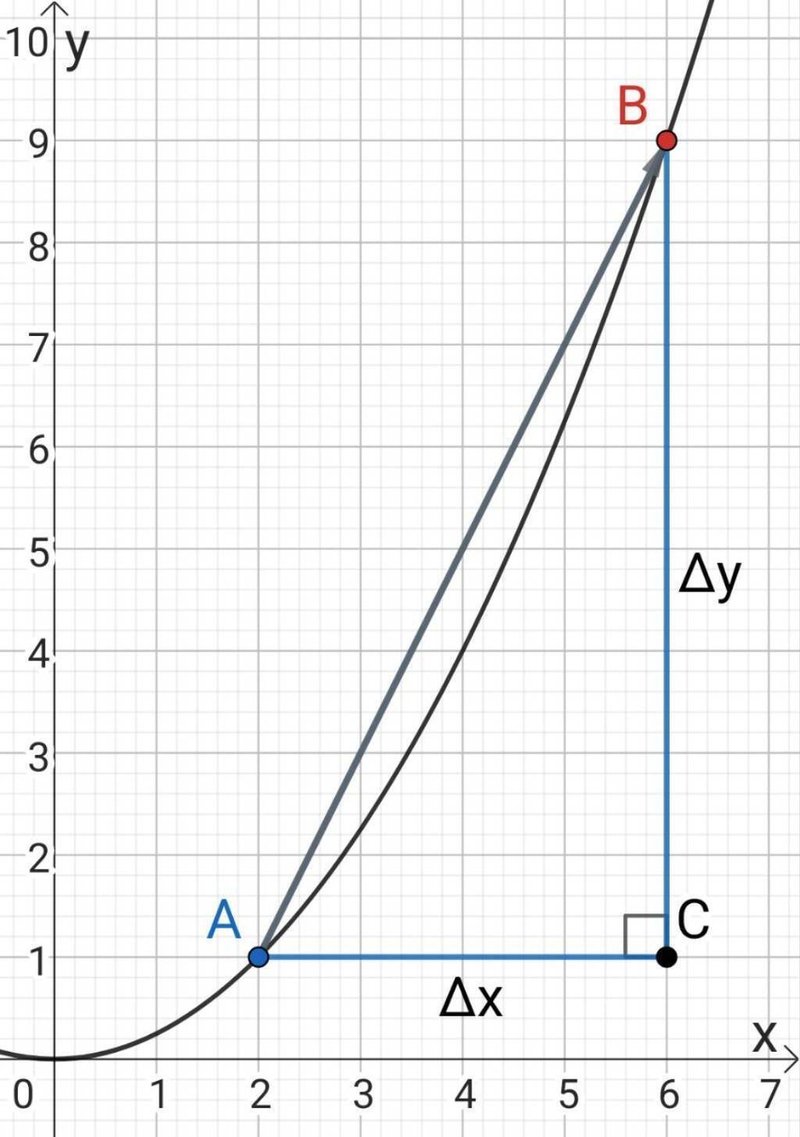
のように、青い点が黒線上を動き、赤い点の場所まで動いた場合を考えてみましょう。
以下では青い点を動かすとき、必ず黒線上を動くとします。
またグラフのように、直角三角形$${ ABC}$$をつくります。
このとき$${ AC}$$、$${ CB}$$はそれぞれ青い点と赤い点の横幅、縦幅となります。
これらからデルタを使って、
横幅$${ =AC=\Delta x}$$
縦幅$${ =CB=\Delta y}$$
と表します。
これら$${ \Delta x}$$と$${ \Delta y}$$を使って、増加量を求めることができます。
増加量とは、ある方向にどれだけ変化したかを表す値です。
$${ x}$$方向に変化した場合は$${ x}$$の増加量と言い、グラフの右方向に動いた場合はプラスの値、左方向に動いた場合はマイナスの値となります。
$${ y}$$方向に変化した場合は$${ y}$$の増加量と言い、グラフの上方向に動いた場合はプラスの値、下方向に動いた場合はマイナスの値となります。
これらから、
$${ x}$$の増加量$${ =\Delta x }$$
$${ y}$$の増加量$${ =\Delta y }$$
となります。

この増加量を座標を使って考えてみましょう。
次の、

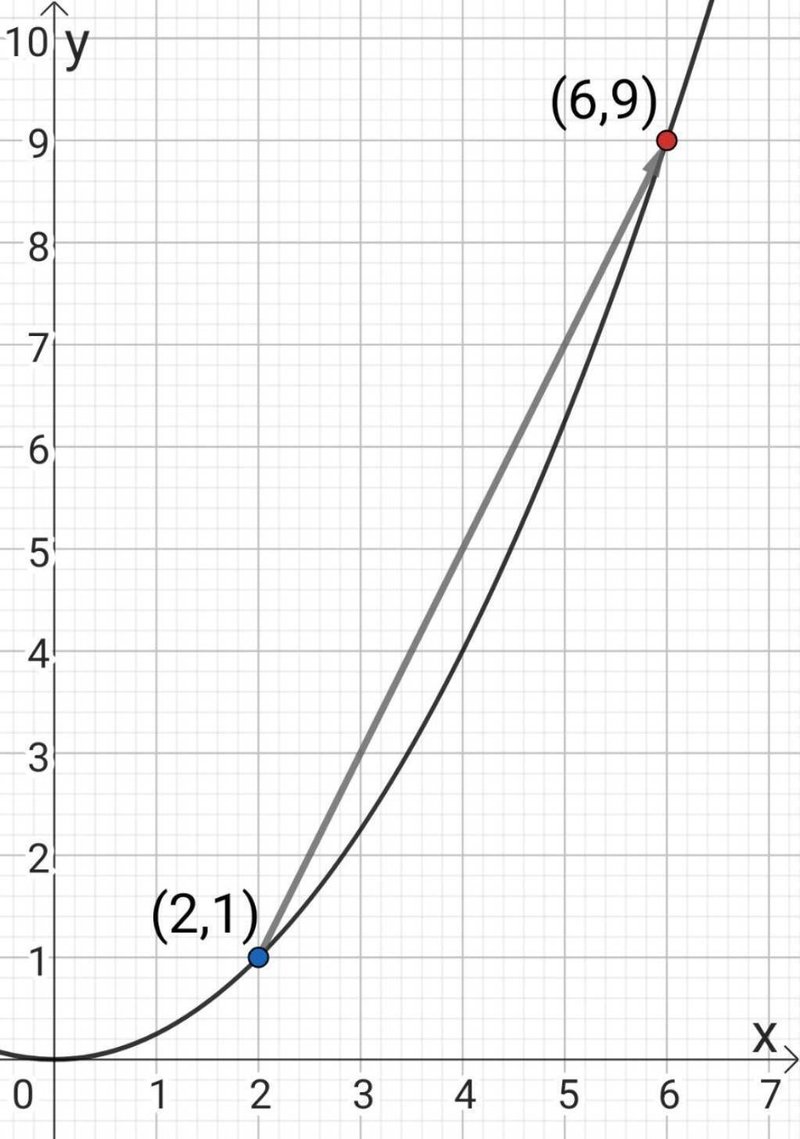
のように青点の座標を$${ (2,1)}$$、赤点の座標を$${ (6,9)}$$とします。
このときも、青い点が黒線上を動き、赤い点の場所まで動いた場合を考えます。
この場合、
$${(2,1) \to (6,9)}$$
と青い点が赤い点まで動くことを、座標と矢印を使って表すことにします。
増加量は、ある方向同士の動いた後の座標から動く前の座標を引くと求められます。
このため、
$${(2,1) \to (6,9)}$$
の各座標の矢印の後ろから前を引いて、
$${ x}$$の増加量$${ =6-2=4}$$
$${ y}$$の増加量$${ =9-1=8}$$
と求められます。
次に青点の座標を$${ (x_1,y_1)}$$、赤点の座標を$${ (x_2,y_2)}$$と文字にして、同じように考えると、
$${(x_1,y_1) \to (x_2,y_2)}$$
と表すことができ、
$${ x}$$の増加量$${ =x_2-x_1}$$
$${ y}$$の増加量$${ =y_2-y_1}$$
となります。
これらから増加量をデルタ、座標を使ってそれぞれ表すと、
$${ x}$$の増加量$${ =\Delta x=x_2-x_1}$$
$${ y}$$の増加量$${ =\Delta y=y_2-y_1}$$
となります。

変化の割合

増加量のときと同じように次の、

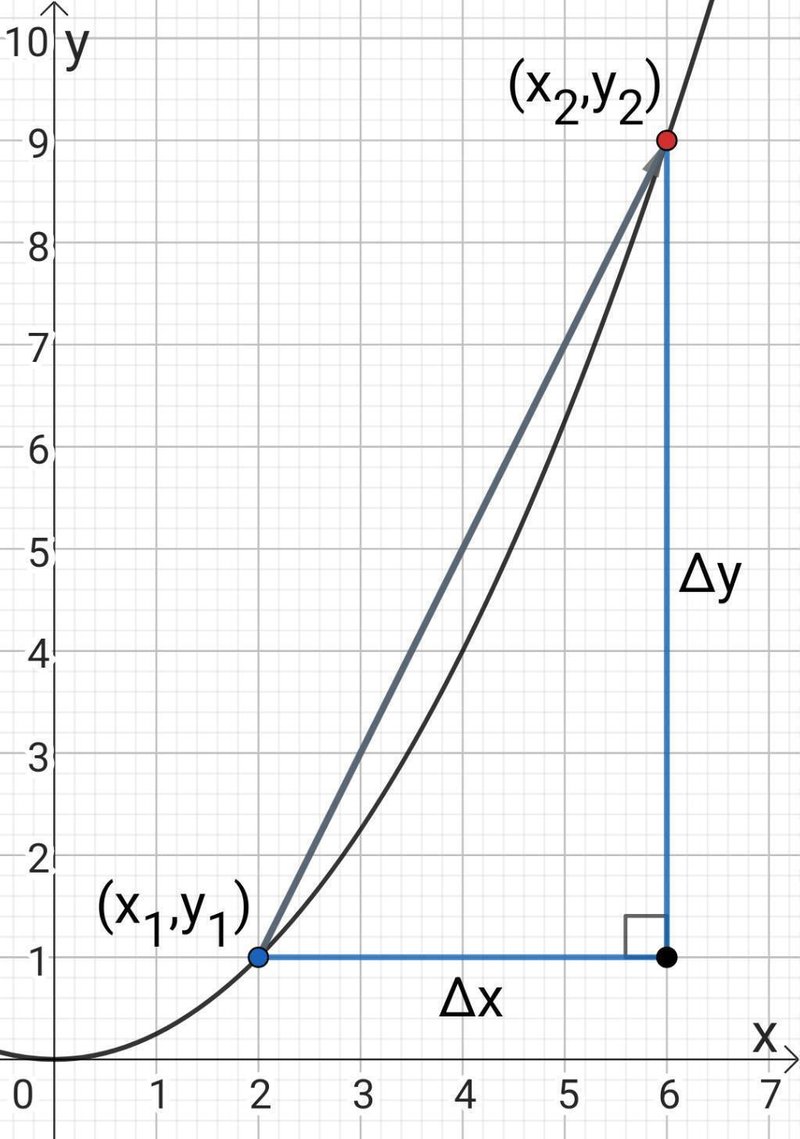
のように、青い点が黒線上を動き、赤い点の場所まで動いた場合を考えてみましょう。
以下では青い点を動かすとき、必ず黒線上を動くとします。
変化の割合とは、$${ x}$$方向に変化したとき$${ y}$$方向にどれだけ変化したかの割合のことです。
また増加量は、$${ x}$$方向または$${ y}$$方向にどれだけ変化したかを表す値です。
これらから、
変化の割合$${ =y}$$の増加量$${ ÷x}$$の増加量
で求めることができます。
増加量はデルタを使うと、
$${ x}$$の増加量$${ =\Delta x }$$
$${ y}$$の増加量$${ =\Delta y }$$
となるので、
変化の割合$${ =\dfrac{ \Delta y}{ \Delta x}}$$
となります。
また座標を使うと増加量は、
$${ x}$$の増加量$${ =x_2-x_1}$$
$${ y}$$の増加量$${ =y_2-y_1}$$
となるので、
変化の割合$${ =\dfrac{ y_2-y_1}{ x_2-x_1}}$$
となります。
これらから変化の割合をデルタ、座標を使って表すと、
変化の割合$${ =\dfrac{ \Delta y}{ \Delta x}=\dfrac{ y_2-y_1}{ x_2-x_1}}$$
となります。

まとめ

今回は、この後の微分の計算で使うデルタ、増加量、変化の割合について解説をしました。
特にデルタは、中学では扱わないので、知らない方やわからない方もいるでしょう。
しかしデルタは、ある方向への幅を表すためによく使われるので、微分・積分でよく使います。

次回は、微分の計算方法について解説をしていきます。
この計算には微分の考え方や、前回と今回の内容を使います。
特に、変化の割合が必要になります。

今後は、ここの内容はわかっているものとして解説をしていきます。
もし、わからなければここを読み直してみてください。