世界の法則を知るために－微分・積分とは？微分の応用例(2)

ある関数$${ y}$$を微分したものである、
$${ \dfrac{d y}{d x}}$$
は接線の傾きとなり、これがプラス、ゼロ、マイナスのどの場合となるかの$${ x}$$の値を調べると、複雑な形のグラフを書くことができます。
今回はこのことを使って、複雑な形のグラフの書き方を解説します。
具体的に最終目標としていた、
$${ y=-2x^2+8x-3}$$
のグラフを書いてみましょう。

複雑な形のグラフの書き方

微分を使うと、

の青線、赤線のような複雑な形のグラフを書くことができます。
これらのようなグラフは、

1. 微分をする

2. 増減表を作る

3. グラフを書く

という手順で書きます。
この増減表や手順について、最終目標としていた、
$${ y=-2x^2+8x-3}$$
を使って、この手順通りにグラフの書き方の解説をします。

微分

次の、
$${ y=-2x^2+8x-3}$$
を微分すると、
$${ \dfrac{d y}{d x}=-4x+8}$$
となります。
この式の右辺がゼロ、プラス、マイナスとなるときの$${ x}$$を求め、増減表を作ります。

増減表

増減表を作るために、
$${ \dfrac{d y}{d x}=-4x+8}$$
の右辺がゼロ、プラス、マイナスとなるときの$${ x}$$を求めます。
このとき、この式の右辺を、
$${ y=-4x+8}$$
としてグラフを書き、グラフから$${ y}$$がゼロ、プラス、マイナスとなるときの$${ x}$$を求めます。
このグラフを書くと、

となります。
このグラフから、黒点のとき$${ y}$$がゼロとなるので、このときの$${ x}$$を求めるには、
$${ -4x+8=0}$$
の方程式を解けば良いとなります。
これを解くと、
$${ x=2}$$
となり黒点の座標は、
$${ (2,0)}$$
となります。
またグラフから、青線のとき$${ y}$$がプラス、赤線のときマイナスとなり、黒点の座標は$${ (2,0)}$$なので、
$${ y}$$がプラスになるとき$${ x<2}$$
$${ y}$$がマイナスになるとき$${ x>2}$$
となることがわかります。
これらをまとめると、

• $${ \dfrac{d y}{d x}}$$がプラスのとき$${ x<2}$$

• $${ \dfrac{d y}{d x}}$$がゼロのとき$${ x=2}$$

• $${ \dfrac{d y}{d x}}$$がマイナスのとき$${ x>2}$$

となります。
これらを、

$$
\begin{array}{c|c}
x & 　  　  　 \\ \hline
\dfrac{d y}{d x} & 　 　  　 \\ \hline
y & 　  　  　 \\
\end{array}
$$

のような表に、
$${ x,\dfrac{d y}{d x},y}$$
についてまとめます。
この表を増減表と呼びます。
この増減表を完成させましょう。
１行目は、
$${ \dfrac{d y}{d x}=0 }$$
となるときの$${ x}$$の値、この両隣には$${ \cdots}$$を書き、

$$
\begin{array}{c|c|c|c}
x & \cdots & 2 & \cdots \\ \hline
\dfrac{d y}{d x} & 　 & 　 & 　 \\ \hline
y & 　 & 　 & 　 \\
\end{array}
$$

とします。
２行目は、
$${ \dfrac{d y}{d x}=0}$$
となるときの$${ x}$$の値の下に$${ 0}$$を書き、

$$
\begin{array}{c|c|c|c}
x & \cdots & 2 & \cdots \\ \hline
\dfrac{d y}{d x} & 　 & 0 & 　 \\ \hline
y & 　 & 　 & 　 \\
\end{array}
$$

とします。
３行目は、
$${ \dfrac{d y}{d x}}$$
の符号、ゼロとなるときの$${ y}$$の値を書きます。
ここで$${ x=2}$$のとき、
$${ y=-2×2^2+8×2-3=-8+16-3=5}$$
となります。
これらから３行目は、

$$
\begin{array}{c|c|c|c}
x & \cdots & 2 & \cdots \\ \hline
\dfrac{d y}{d x} & 　 & 0 & 　 \\ \hline
y & + & 5 & - \\
\end{array}
$$

となります。
２行目の残りは３行目で、
$${ \dfrac{d y}{d x}}$$
の符号が、プラスのときは$${\nearrow}$$、マイナスのときは$${\searrow}$$を書き、

$$
\begin{array}{c|c|c|c}
x & \cdots & 2 & \cdots \\ \hline
\dfrac{d y}{d x} & \nearrow & 0 & \searrow \\ \hline
y & + & 5 & - \\
\end{array}
$$

となります。
ここで、$${\nearrow}$$は$${ y}$$が増えていくこと、$${\searrow}$$は$${ y}$$が減っていくことを表しています。
これで増減表が完成となります。
この増減表から、グラフを書くことができます。

グラフ

増減表、

$$
\begin{array}{c|c|c|c}
x & \cdots & 2 & \cdots \\ \hline
\dfrac{d y}{d x} & \nearrow & 0 & \searrow \\ \hline
y & + & 5 & - \\
\end{array}
$$

を使って、グラフを書いてみましょう。
まず、
$${ \dfrac{d y}{d x}=0 }$$
となるときの点をグラフに書きます。
この点の座標は増減表、

$$
\begin{array}{c|c|c|c}
x & \cdots & \boxed{2} & \cdots \\ \hline
\dfrac{d y}{d x} & \nearrow & 0 & \searrow \\ \hline
y & + & \boxed{5} & - \\
\end{array}
$$

の四角で囲んだ部分から$${ (2,5)}$$となります。
これを、

の黒点で表したようにグラフに書きます。
この点が$${ y}$$の増減の境目となるので、増減表から$${ (2,5)}$$の左右で$${ y}$$が増えるか減るかを見ます。
$${ y}$$の増減は増減表、

$$
\begin{array}{c|c|c|c}
x & \cdots & 2 & \cdots \\ \hline
\dfrac{d y}{d x} & \boxed{\nearrow} & 0 & \boxed{\searrow} \\ \hline
y & + & 5 & - \\
\end{array}
$$

の四角で囲んだ部分から、境目である黒点の、
左側は$${ \nearrow}$$なので増える
右側は$${ \searrow}$$なので減る
となります。
これらからグラフは、

となります。

確認

増減表、

$$
\begin{array}{c|c|c|c}
x & \cdots & 2 & \cdots \\ \hline
\dfrac{d y}{d x} & \nearrow & 0 & \searrow \\ \hline
y & + & 5 & - \\
\end{array}
$$

とグラフの確認をするため、
$${ y=-2x^2+8x-3}$$
と、この式を微分した、
$${ \dfrac{d y}{d x}=-4x+8}$$
の右辺を、
$${ y=-4x+8}$$
としたときのグラフを見てみましょう。
以下では、
$${ y=-2x^2+8x-3}$$
を曲線のグラフ、
$${ y=-4x+8}$$
を直線のグラフと言います。
これらのグラフは、

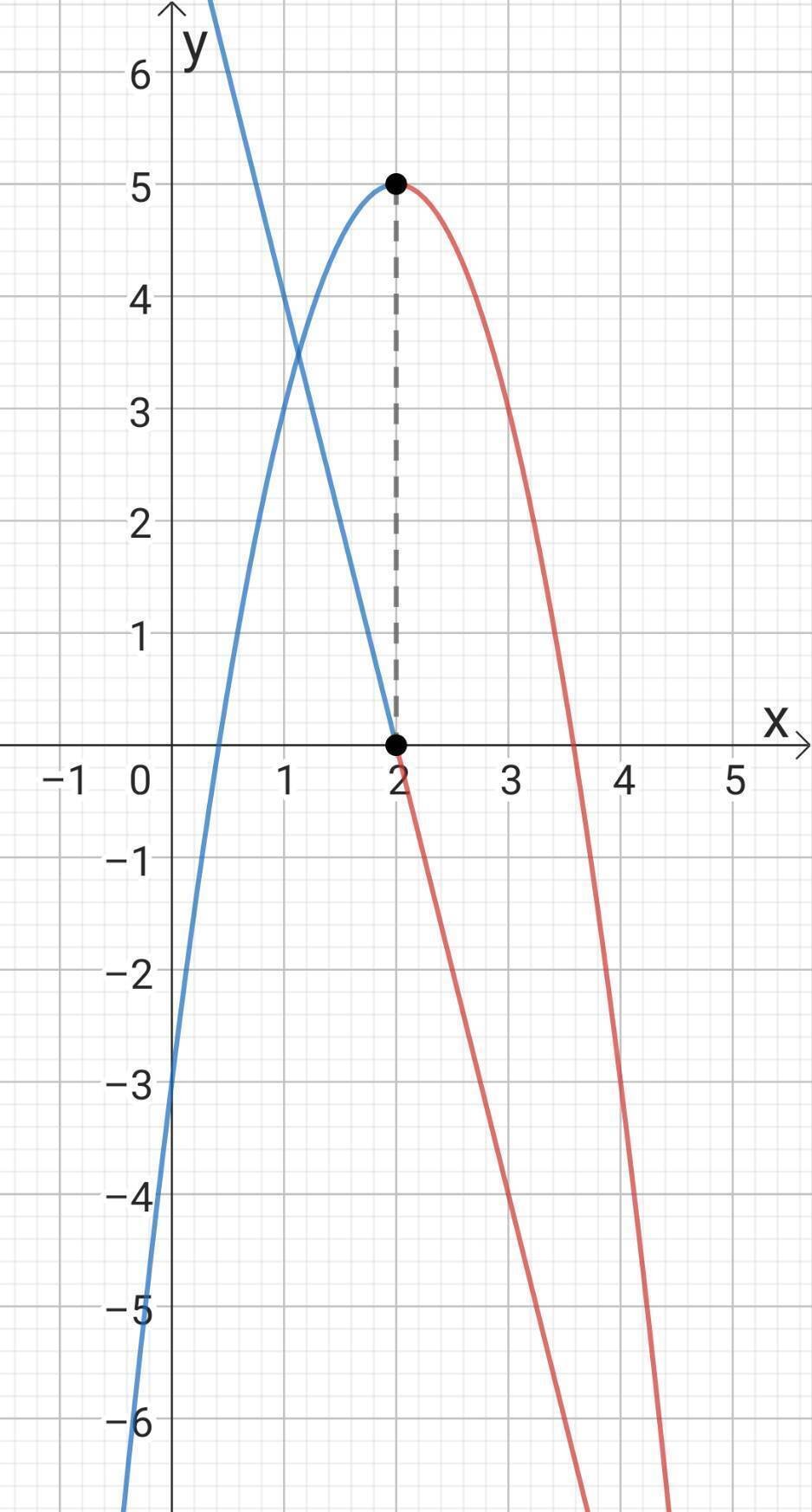
のようになります。
このグラフから、

• 曲線のグラフの黒点は、増減の境目となっていること

• 直線のグラフの黒点は、$${ y}$$の値がゼロとなっていること

• ２つの黒点の$${ x}$$座標は同じになっていること

がわかります。
また、

• 黒点の左側である青線は、曲線のグラフでは$${ y}$$が増えていて、直線のグラフでは$${ y}$$がプラスになっていること

• 黒点の右側である赤線は、曲線のグラフでは$${ y}$$が減っていて、直線のグラフでは$${ y}$$がマイナスになっていること

がわかります。
これらから増減表、グラフが正しいことがわかります。

まとめ

今回は最終目標としていた、
$${ y=-2x^2+8x-3}$$
のグラフを書きました。
このとき、この式を微分して増減表を作り、この表からグラフを書きました。
この増減表は、複雑な形のグラフを書くために、よく使います。
今回で微分の応用例は終わりとなります。
次回は、積分の応用例について書きます。