世界の法則を知るために－微分・積分とは？積分の応用例(1)

積分により、いろいろな面積を求めることができます。
このいろいろな面積を求められることから、例えば等速直線運動ではなく、速さがいろいろな変化をする場合の距離を求められます。
この例のように積分は、物理で使われることがありますが、積分を利用すると他にも求められるものがあります。
この積分の応用例では積分を利用した他の求められるものの例として、回転体の体積の求め方について解説します。
また、回転体の体積の求め方の具体例として円柱、円錐、球の体積を求めます。
特に球の体積は公式を覚えただけで、なぜ公式のようになるかわからないと思います。
また、球の体積と表面積は微分・積分と深い関係があり、このことを使うと球の表面積を求めることもできます。
これらから積分の応用例の最終目標は、球の体積と表面積の公式を求めることとします。

復習

ここでは回転体とは何か、積分の考え方の復習をします。
これらは、回転体の体積を求めるために必要な内容となります。

回転体

次の、

の黒線のようなある関数$${ y}$$、青色部分のようなある関数$${ y}$$と$${ x}$$軸で囲まれた部分の、$${ x}$$が$${ a}$$から$${ b}$$までの範囲を考えます。
この黒線のある関数$${ y}$$は、真横の直線を表しています。
また青色部分を、$${ x}$$軸のまわりに一回転させると円柱になります。
このように、青色部分のようなある関数$${ y}$$と$${ x}$$軸で囲まれた部分の、$${ x}$$が$${ a}$$から$${ b}$$までの範囲をある直線のまわりに一回転させてできた立体を回転体と言い、この回転体の体積を考えます。
以下ではグラフの、黒線をある関数$${ y}$$とします。
また青色部分は、黒線と$${ x}$$軸で囲まれた部分の、$${ x}$$が$${ a}$$から$${ b}$$までの範囲とします。

積分の考え方

積分の考え方の復習のため次の、

の青色部分の面積を考えます。
積分では青色部分を、

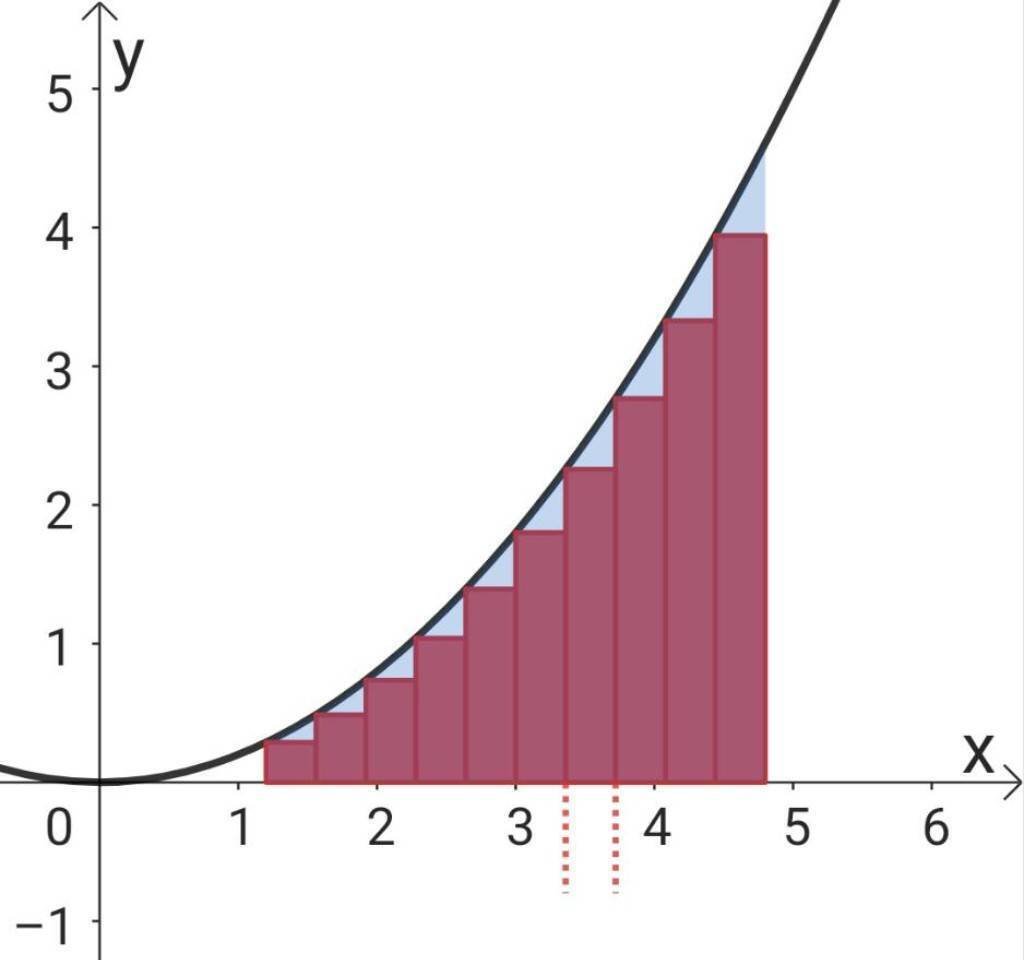
のように赤い長方形で分割し、赤い点線間の距離のような横幅$${ \Delta x}$$を、
ゼロに限りなく近づけたとき
を考えると、赤い長方形の面積と青色部分の面積は同じになります。
この青色部分の面積は、
$${\displaystyle \int_a^b{ydx}}$$
のように定積分を使った式で表すことができます。
この定積分の式は、ある関数$${ y}$$と$${ x}$$軸で囲まれた部分を表しているため、
$${\displaystyle \int_a^b{\boxed{y}d\boxed{x}}}$$
の四角で囲んだ部分となっています。
また、$${ x}$$が$${ a}$$から$${ b}$$までの範囲の面積となるため、
$${\displaystyle \int_{\boxed{a}}^{\boxed{b}}{yd\boxed{x}}}$$
の四角で囲んだ部分となっています。

回転体の体積の求め方

回転体の体積の求め方を解説するため、定積分の式の他の見方について解説をします。
このことと復習の内容を使って、回転体の体積の求め方の解説をします。
以下でもグラフの、黒線をある関数$${ y}$$とします。
また青色部分は、黒線と$${ x}$$軸で囲まれた部分の、$${ x}$$が$${ a}$$から$${ b}$$までの範囲とします

他の見方

定積分の式、
$${\displaystyle \int_a^b{ydx}}$$
の見方を変えてみましょう。
次の、

の青色部分を、

のように赤い長方形に分割して、青色部分の面積を考えます。
ここで、赤い点線間の距離である横幅は赤い長方形の横の長さで、これを$${ \Delta x}$$とします。
このとき、

のように、赤い長方形の１つを抜き出し、この面積を考えます。
この赤い長方形の縦の長さは$${ y}$$となり、横の長さは$${\Delta x}$$なので、この長方形の面積は、
$${y \Delta x}$$
となります。
ここで横の長さである$${\Delta x}$$を、
ゼロに限りなく近づけたとき
を考えると、
$${y dx}$$
のように、$${\Delta}$$を$${d}$$に置き換えることができます。
また、

のように青色部分の面積は、分割した赤い長方形の面積を、$${ x}$$が$${ a}$$から$${ b}$$までの範囲の全てを足すので、
$${y dx}$$
に、
$${\displaystyle \int_a^b}$$
を書き加えると定積分の式、
$${\displaystyle \int_a^b{ydx}}$$
となります。
この後に上端、下端である$${ a,b}$$が、
$${\displaystyle \int_a^b{yd\boxed{x}}}$$
の四角で囲んだ部分の文字の範囲となっているか確認をします。
これは、$${ a}$$から$${ b}$$までの範囲になるから、
$${\displaystyle \int_a^b}$$
を書き加えるだけと考えていると、$${ a,b}$$が$${ x}$$以外の範囲のとき、
$${\displaystyle \int_a^b{ydx}}$$
として間違いとなる場合があります。
今回の定積分の式、
$${\displaystyle \int_a^b{ydx}}$$
は、$${ a,b}$$が$${ x}$$の範囲のときなので、正しい式となります。

体積の求め方

次の、

の青色部分を、$${ x}$$軸のまわりに一回転させた回転体の体積を考えてみましょう。
このとき青色部分を、

のように赤い長方形に分割します。
ここで、

のように、赤い長方形の１つを抜き出して考えます。
この赤い長方形を、$${ x}$$軸のまわりに一回転させると、

• 底面の半径が$${ y}$$

• 高さが$${ \Delta x}$$

の円柱となります。
この円柱の体積は、
$${ \pi × y^2 × \Delta x=\pi y^2 \Delta x}$$
となります。
ここで、円柱の高さである$${ \Delta x}$$を、
ゼロに限りなく近づけたとき
を考えると、
$${ \pi y^2 d x}$$
となります。
また、

の青色部分を$${ x}$$軸のまわりに一回転させた回転体の体積は、分割した赤い長方形を$${ x}$$軸のまわりに一回転させた回転体の体積を、$${ x}$$が$${ a}$$から$${ b}$$までの範囲の全てを足したものとなるので、
$${ \pi y^2 d x}$$
に、
$${\displaystyle \int_a^b}$$
を書き加えると、
$${\displaystyle \int_a^b{\pi y^2 dx}}$$
となります。
この式が、青色部分を$${ x}$$軸のまわりに一回転させた回転体の体積を求める式となります。
この式の確認をしましょう。
この式では上端、下端である$${ a,b}$$が、
$${\displaystyle \int_a^b{\pi y^2 d\boxed{x}}}$$
の四角で囲んだ部分の文字である$${ x}$$の範囲となっているので、この式が正しいことがわかります。

まとめ

今回は回転体と積分の考え方の復習をし、定積分の式の他の見方から、積分の応用例として回転体の体積の求め方について解説をしました。
ある関数$${ y}$$と$${ x}$$軸で囲まれた部分の、$${ x}$$が$${ a}$$から$${ b}$$までの範囲を、$${ x}$$軸のまわりに一回転させた回転体の体積を$${ V}$$とすると、
$${\displaystyle V=\int_a^b{\pi y^2 dx}}$$
となり、定積分を使って回転体の体積を求めることができます。
次回は具体例として、
$${\displaystyle V=\int_a^b{\pi y^2 dx}}$$
を使って円柱、円錐の体積を求めます。