世界の法則を知るために－微分・積分とは？微分・積分の応用例(3)

微分方程式を使って斜方投射の問題を解くと、二次関数が放物線となる理由がわかります。
このため前回は理科の内容の解説として、主に運動方程式について解説をしました。
今回は最終目標としていた、二次関数が放物線となる理由の解説をします。

斜方投射

次の、

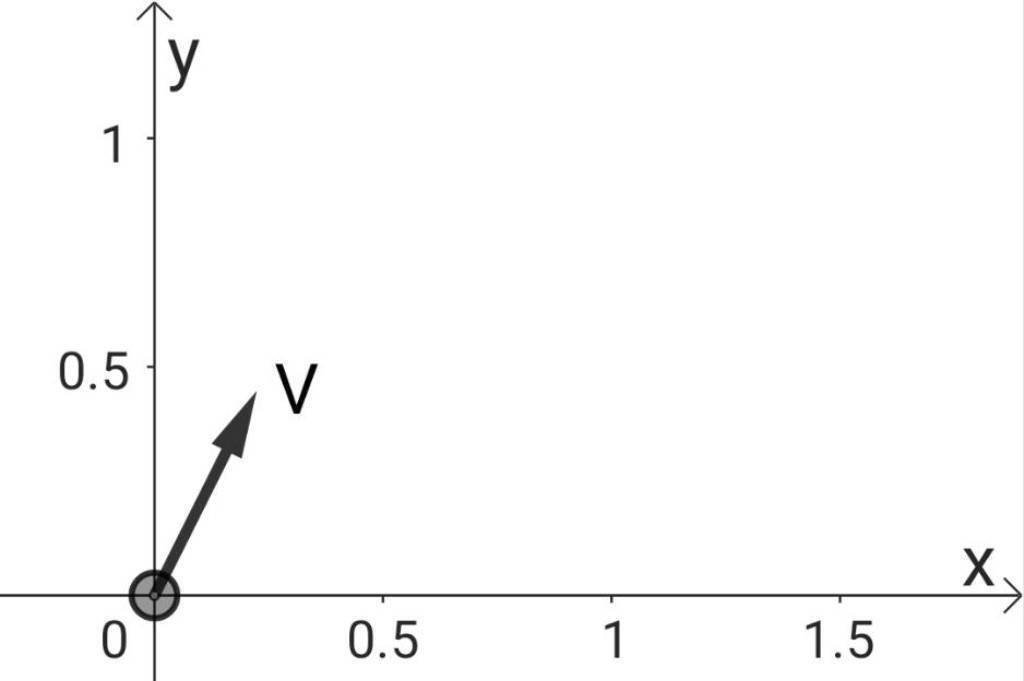
のように時刻$${ t}$$が$${ 0}$$のとき、点$${ (0,0)}$$にある質量$${ m}$$の小球を、斜め方向に速さ$${ V}$$で投げた場合である斜方投射を考えます。
ここで、

のように、ある時刻$${ t}$$のときの速さを$${v}$$、力を$${F}$$とします。
また、ある時刻$${ t}$$のときの$${ x}$$方向、$${ y}$$方向の$${ (0,0)}$$からの距離をそれぞれ$${ x}$$、$${ y}$$とします。
このとき斜め方向を考えているため、$${v,F }$$を$${ xy}$$方向に分解すると運動方程式は、
$${\displaystyle \dfrac{dv_x}{dt}=\dfrac{F_x}{m},\dfrac{dv_y}{dt}=\dfrac{F_y}{m}}$$
となります。
また$${ x}$$方向の距離と速さ$${ x,v_x}$$、$${ y}$$方向の距離と速さ$${ y,v_y}$$から、
$${\displaystyle  \dfrac{dx}{dt}=v_x,\dfrac{dy}{dt}=v_y}$$
となり、これらを以下では距離と速さの関係式と言います。
これらの式から、二次関数が放物線となる理由の解説をします。

斜方投射の運動方程式と解

斜方投射のとき運動方程式は、
$${\displaystyle \dfrac{dv_x}{dt}=\dfrac{F_x}{m},\dfrac{dv_y}{dt}=\dfrac{F_y}{m}}$$
となります。
この場合の$${ F_x,F_y}$$を求めてみましょう。
$${ x}$$方向には力が働いていないので、
$${ F_x=0}$$
となります。
$${ y}$$方向には重力が働いているので、
$${ F_y=-G=m×(-g)=-mg}$$
となります。
ここで$${G,g }$$の符号は、$${ y}$$軸方向の逆である真下となるのでマイナスとなります。
これらを、
$${\displaystyle \dfrac{dv_x}{dt}=\dfrac{F_x}{m},\dfrac{dv_y}{dt}=\dfrac{F_y}{m}}$$
に代入すると、
$${\displaystyle \dfrac{dv_x}{dt}=\dfrac{0}{m},\dfrac{dv_y}{dt}=\dfrac{-mg}{m}}$$
となり、
$${\displaystyle \dfrac{dv_x}{dt}=0,\dfrac{dv_y}{dt}=-g}$$
となります。
これらの微分方程式の解は、右辺を不定積分して、
$${\displaystyle v_x=\int{0dt},v_y=\int{-gdt}}$$
となります。
これらは、$${ g}$$が定数であることに注意して計算すると、
$${\displaystyle v_x=C_x, v_y=-gt+C_y}$$
となります。
ここで、$${ C_x,C_y}$$は各式の積分定数としています。
これら$${ C_x,C_y}$$を求めます。
この斜方投射では、$${ t=0}$$のとき$${ v=V}$$としています。
$${ V}$$を$${ xy}$$方向に分解すると、
$${ t=0}$$のとき$${ v_x=V_x,v_y=V_y}$$
となります。
このとき$${ V}$$は定数なので、$${ V_x,V_y}$$も定数となります。
これらから、
$${ t=0}$$のとき$${ v_x=V_x,v_y=V_y}$$
を、
$${\displaystyle v_x=C_x, v_y=-gt+C_y}$$
に代入すると、
$${\displaystyle V_x=C_x, V_y=-g×0+C_y=C_y}$$
となり、
$${\displaystyle C_x=V_x, C_y=V_y}$$
となります。
これらを、
$${\displaystyle v_x=C_x, v_y=-gt+C_y}$$
に代入すると、
$${\displaystyle v_x=V_x, v_y=-gt+V_y}$$
となります。
また距離と速さの関係式から、
$${\displaystyle  \dfrac{dx}{dt}=v_x,\dfrac{dy}{dt}=v_y}$$
となるので、
$${\displaystyle v_x=V_x,v_y=-gt+V_y}$$
を代入すると、
$${\displaystyle  \dfrac{dx}{dt}=V_x,\dfrac{dy}{dt}=-gt+V_y}$$
となります。
これらの微分方程式の解は、右辺を不定積分して、
$${\displaystyle x=\int{V_xdt},y=\int{\left( -gt+V_y \right)dt}}$$
となります。
これらは、$${ V_x,V_y,g}$$が定数であることに注意して計算すると、
$${\displaystyle x=V_xt+D_x,y=-\dfrac{1}{2}gt^2+V_yt+D_y}$$
となります。
ここで、$${ D_x,D_y}$$は各式の積分定数としています。
これら$${ D_x,D_y}$$を求めます。
この斜方投射では、$${ t=0}$$のとき$${ x=0,y=0}$$としています。
これらを、
$${\displaystyle x=V_xt+D_x,y=-\dfrac{1}{2}gt^2+V_yt+D_y}$$
に代入すると、
$${\displaystyle 0=V_x×0+D_x}$$
$${0=-\dfrac{1}{2}g×0^2+V_y×0+D_y}$$
となり、
$${\displaystyle D_x=0, D_y=0}$$
となります。
これらを、
$${\displaystyle x=V_xt+D_x,y=-\dfrac{1}{2}gt^2+V_yt+D_y}$$
に代入すると、
$${\displaystyle x=V_xt,y=-\dfrac{1}{2}gt^2+V_yt}$$
となります。
これらの式から、$${ y}$$を$${ x}$$の式で表すことを考えます。
まず、
$${\displaystyle x=V_xt}$$
の両辺を$${ V_x}$$で割ると、
$${\displaystyle t=\dfrac{x}{V_x}}$$
となります。
これを、
$${\displaystyle y=-\dfrac{1}{2}gt^2+V_yt}$$
に代入して計算をすると、
$${\displaystyle y=-\dfrac{1}{2}g \left( \dfrac{x}{V_x}  \right)^2+V_y \left( \dfrac{x}{V_x} \right)}$$
　$${\displaystyle =-\dfrac{g}{2V_x^2} x^2 + \left( \dfrac{V_y}{V_x} \right)x}$$
となります。
$${ g,V_x,V_y}$$は定数なので、この式の各係数は定数となります。
これらの各係数を、
$${\displaystyle a=\dfrac{g}{2V_x^2},b=\dfrac{V_y}{V_x}}$$
とすると、
$${ y=-ax^2+bx}$$
となります。
この式から斜方投射のとき、$${ (0,0)}$$からの距離である$${ x,y}$$の関係式が、二次関数となっていることがわかります。
これらから、斜方投射の軌道である放物線は二次関数となることがわかります。

まとめ

今回は斜方投射の運動方程式を解き、最終目標としていた二次関数が放物線となる理由の解説をしました。
このことは、運動方程式のような微分方程式からわかります。
他にも、微分方程式からいろいろなことがわかるため、微分方程式は数学の中で最も重要なものの１つとなります。
今回で、応用例の全てが終わりとなります。
また、次回のあとがきで微分・積分について終わりとなります。