
柔らかい幾何学1(オイラー数、オイラーの公式)
※この記事はあまり厳密な議論をしないようにします。
0.はじめに
・下の三角形1つからなる平面グラフについて考えてみよう。これの頂点の数は3つ、辺の数は3つ、領域の数は2つである。(今回はグラフの外側の領域もカウントすることにする)

・さて、この平面グラフに次のように点と辺を付け足して2つの三角形からなる平面グラフを作る。この平面グラフの頂点の数は4個、辺の数は5個、領域の数は3個となる。

・一見すると、先ほどの平面グラフとこの平面グラフの共通点はないように見えるが、実は
(頂点の個数)ー(辺の個数)+(領域の個数)
を計算するとどちらも2であることがわかる。実際、最初の平面グラフの場合は3-3+2=2だし、その次の平面グラフも4-5+3=2となる。ではさらに点と辺を付け足して3つの三角形からなる平面グラフを作ると、これに関しても(頂点の個数)ー(辺の個数)+(領域の個数)=2を満たす。

・一般に、$${n}$$個の三角形からなる平面グラフに関しても(頂点の個数)ー(辺の個数)+(領域の個数)=2が成り立つ。ざっくりと証明すると、($${n-1}$$)個の三角形からなる平面グラフに点と辺を付け足して、$${n}$$個の三角形からなる平面グラフを作るときに、頂点は1つ、辺は2つ、領域は1つ増えるので、上の式の値は点と辺を付け足しても変わらない(証明終)。
・今は、いくつかの三角形からなる平面グラフだけを考えていたが、実は三角形でないものでも成立する。以下はそれについて説明する。
1.言葉の定義
・連結平面グラフ
有限個の点とそれらを結ぶ辺からなり、辺同士の交差はなく、連結成分が1であるもの.
例(連結平面グラフの例)

・H変形(専門用語ではない)
辺を(交差が起こらないように)グネグネ変形したり、2点とそれを結ぶ辺を1点に縮めたり、逆に1点から2点とそれらを結ぶ辺に広げたりする変形.
例(H変形の例、H変形じゃない例)

・$${\bm{n}}$$-ブーケ
1つの点と$${n}$$本の辺からなる連結平面グラフを$${n}$$-ブーケという.($${n}$$の指定がない場合は単にブーケという)
例($${n}$$-ブーケの例)

$${n}$$-ブーケの定義から、次は明らかである:
「$${\bm{n}}$$と$${\bm{m}}$$が異なるなら$${\bm{n}}$$-ブーケから$${\bm{m}}$$-ブーケにH変形することはできない」
さらにここで一つの命題を紹介する(証明は省くが、証明には上の事実を用いる):
「任意の連結平面グラフは、ある唯一の$${\bm{n}}$$-ブーケに変形できる」

問1:次の連結平面グラフをH変形して、$${n}$$-ブーケにせよ.
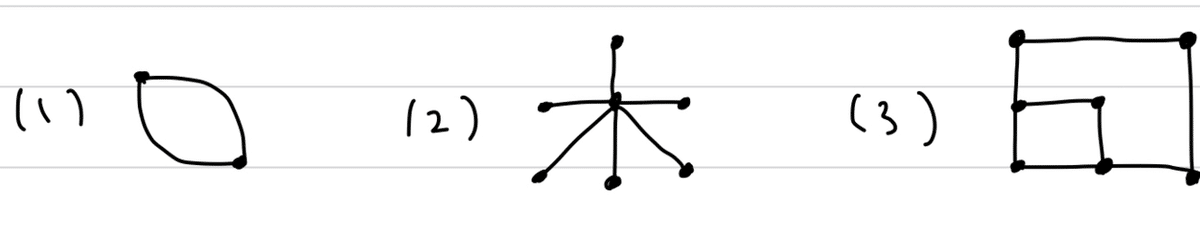
・H同値(専門用語で言うとホモトピー同値に該当する同値性)
連結平面グラフ$${G_1}$$と$${G_2}$$が共に$${n}$$-ブーケにH変形できるなら、$${G_1}$$と$${G_2}$$はH同値であるといい、$${\bm{G_1\simeq G_2}}$$とかく.
(大学数学を勉強している方向け;問:H同値は同値関係であることを示せ)
問2:次のうち、連結平面グラフ(*)とH同値であるものを選べ.

2.オイラー数
・オイラーの公式を述べる前にまずオイラー数というものを紹介する.
・連結平面グラフ$${G}$$の点の数を$${V(G)}$$、辺の数を$${E(G)}$$とした時、
$${\chi (G):=V(G)-E(G)}$$を$${G}$$のオイラー数という.
ここで次の命題を紹介する:
「連結平面グラフ$${\bm{G,G’}}$$がH同値ならば$${\bm{\chi (G)=\chi(G’)}}$$が成立する.またその逆も成立する」
(ざっくりと証明)
$${G}$$と$${G’}$$はH同値なので、(少し考えればわかるが)$${G}$$からH変形することで$${G’}$$が得られることがわかる.
H変形の定義を見返すと、
①$${G}$$の各辺がグネグネ変形
②$${G}$$の異なる2点とそれを結ぶ辺を1点に収縮
③$${G}$$の1点を異なる2点とそれを結ぶ辺に拡張
の3種類の操作からなる.それぞれの操作を施した時の点と辺の数を見ると、
①点、辺の数共に変わらない
②点、辺の数共に1つ減る
③点、辺の数共に1つ増える

これより、H変形によりオイラー数は変わらないことがわかった.逆が成り立つことについては省略.
問3:問2の4つの連結平面グラフのオイラー数を求めよ
3.連結平面グラフにおけるオイラーの公式
・オイラー数を定義するときは連結平面グラフの点の数と辺の数を用いた。対してオイラーの公式では、点、辺の数に加えてグラフが分ける領域の数$${F(G)}$$を考慮した式となる。
・この「連結平面グラフが分ける領域」には、下の例のようにグラフの外側の無限に広がる部分も1つの領域とカウントする。すなわち、領域の数は必ず1以上の整数になる。
・以上を踏まえた上でオイラーの公式を述べる:
「任意の連結平面グラフGに対し、$${\bm{V(G)-E(G)+F(G)=2}}$$が成り立つ」
これの証明を述べる前にいくつか例を示す。

(オイラーの公式の証明(ざっくりめ))
・$${E(G)}$$に関する数学的帰納法を用いて示す。
・まず$${E(G)=0$$}のとき、$${G}$$は一点からなるグラフとなるため、$${V(G)=1,F(G)}$$よりオイラーの公式が成り立つ。
・次に$${E(G)=n}$$であるいかなる連結平面グラフ$${G}$$がオイラーの公式を満たすときに、$${E(G’)=n+1}$$である連結平面グラフ$${G’}$$もオイラーの公式を満たすことを示す。
(i)点の数が2以上のとき

(ii)点の数が1のとき(すなわち$${(n+1)}$$-ループであるとき)

4.補足:高校で習うオイラーの公式について
・以上の議論では、連結平面グラフ版オイラーの公式を紹介したが、高校で習うオイラーの公式は(3次元)凸多面体版である.
・実は立体射影を用いるとれ連結平面グラフ版オイラーの公式から凸多面体版オイラーの公式が導かれる.これについて少し述べる.
4.1.立体射影について(紹介だけ)
・単位球$${S^2=\{(x,y,z)\in \mathbb{R} |x^2+y^2+z^2=1\}}$$と点$${N(0,0,1)}$$、$${S^2}$$上の$${N}$$以外の点$${A}$$について、直線$${NA}$$と$${xy}$$平面の交点の$${(x,y)}$$座標を$${p(A)\in \mathbb{R}^2}$$とする.このとき、写像$${p:S^2\backslash \{N\} \rightarrow \mathbb{R}^2}$$を立体射影(stereographic projection)という.大事な事実として、立体射影は全単射(1対1対応)である.

4.2.連結球面グラフ
・ここで立体射影$${p}$$を用いて連結球面グラフを定義する:
「$${G_{S^2} \subset S^2\backslash \{N\}}$$に対し、$${p(G_{S^2})}$$が連結平面グラフであるとき、$${G_{S^2}}$$を連結球面グラフであるという.
・連結球面グラフ$${G_{S^2}}$$の点、辺、領域の数は連結平面グラフのときと同じ記号$${V(G_{S^2}),E(G_{S^2}),F(G_{S^2})}$$を用いる.
・$${p}$$は全単射なので$${V(G_{S^2})=V(p(G_{S^2})),E(G_{S^2})=E (p(G_{S^2})),F(G_{S^2})=F(p(G_{S^2}))}$$が成り立つ.すなわち、連結球面グラフに関してもオイラーの公式が成り立つ.
4.3.凸多面体版オイラーの公式
・次に単位球$${S^2}$$にすっぽり覆われるような凸多面体Pを考える.この凸多面体Pの内部の1点(例えば重心とか)に光源を設置し、Pの頂点や辺を単位球に投影する
(ただしここで点$${N(0,0,1)}$$に頂点や辺が投影されないように予め凸多面体Pは調整されているものとする).
・すると、単位球に投影されたPの頂点や辺は連結球面グラフになるから、オイラーの公式が成立.「投影」というのは全単射であるから、多面体Pに対してもオイラーの公式が成り立つ.
最後の方はかなり雑な説明になってしまったが、以上.
追記:参考文献
枡田幹也、代数的トポロジー、朝倉書店、2002年
よろしければサポートをお願いします。いただいたサポートは、数学書の購入といった、今後の執筆にあたり必要となる費用に充てる予定です。
