回転とは何か:物理数学:群論の触り

前回までのお話物理は量子力学がもつ直感的でない現象の話をしてきた．どれほど直感的でない帰結でも実験で確かめられてしまった以上，現実は変な世界なのだった．世界は量子力学を正しいと言っている．

これから数回(?)に渡って量子力学から離れて少し数学の話をしようと思う．数学といっても数学者から見ればガバガバで聞くに絶えないかもしれないが直感的な理解と物理のイメージを重視する．致命的な誤りがあれば指摘してほしい．

なぜわざわざ数学の話をするかといえば，物理は数学の言葉で書かれているからだ．言葉を持たぬものが人に何かを伝え，受け取るのは難しい．

これから話すのは"群論(ぐんろん)"と呼ばれるものの触りだ．掛け算の一般化なのだが，物理の世界では対称性とよく結びつき，その理解が素粒子や原子核の物理を理解する上で必要だ．計算する上では必要なのだが，お話の上で必要か今ひとつはっきりしない．あとで必要になる前にあらかじめ用意しておこうと言う算段だ．

では話を始めよう．早速だが質問だ．回転とは何か？一言で表すならば何だろうか．

------

辞書を引いてみるか〜．

回転（かいてん）
１ 物が、ある軸を中心としてまわること。
https://dictionary.goo.ne.jp/word/%E5%9B%9E%E8%BB%A2/#jn-36598

ふんふん，まわる...．

回る（まわる）
１ 軸を中心にして円を描くように動く。回転する。
https://dictionary.goo.ne.jp/word/%E5%9B%9E%E3%82%8B_%28%E3%81%BE%E3%82%8F%E3%82%8B%29/#jn-210283

おい循環論法じゃねぇか！！！！やっぱり国語辞典はダメだな．

じゃあ僕の理解を話そう．回転とは

平行移動を除いて，微小変換の繰り返しで作れる，長さを変えない変換

だ．もっと具体的にいえば，伸び縮みしない棒の片方を固定して，もう一方を動かしてできる変換の全てだ．この中で回転でないものは絶対にない(はず)．

これを理解していれば今日の話は終わりだ．正しくはこれを数学の言葉で話して終わりにしよう．

最も次元の低い，回転の定義できる空間は二次元だ．今日は二次元の話をしよう．また，回転される対象は最も簡単なベクトル(矢印)を扱う．

早速だがこの中で赤の矢印を回転して移れる矢印はどれだろう．

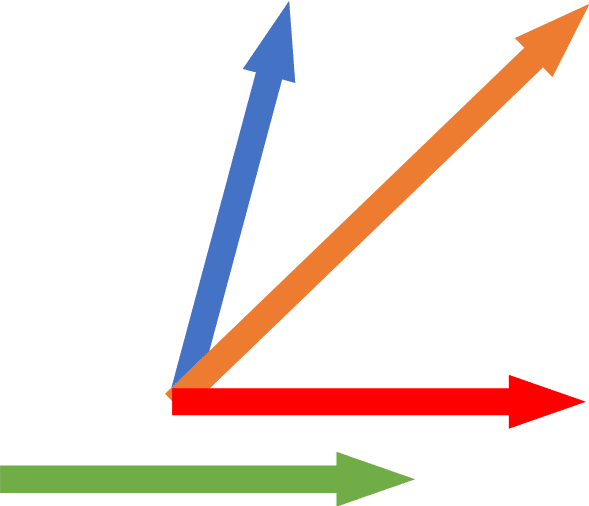
青が回転で移れる矢印だ．他は回転ではない．緑は長さも向きも変わっていないが平行移動している．オレンジは根元は揃っているが長さが変わっている．青は根元が揃って，かつ長さが同じ矢印なのだ．

長さを変えず，根元を変えないで，回転でないものがある．それは裏返す行為だ．ただの矢印では表せないが，三角形などを例に取ればイメージできるだろう．三つの頂点それぞれの長さを変えずに，ひっくり返せば青から赤にできるが，長さを変えないまま少しずつ変形させていっても裏返しにはできない．

先の回転の定義が，直感的に理解できただろうか．

平行移動を除いて，微小変換の繰り返しで作れる，長さを変えない変換

さて日本語では回転を決められたが数学の言葉ではどうなるのだろう．と言うかこんなまどろっこしい言い方でなく簡単な表現がないだろうか．ある．

n次元回転とはSO(n)群で表現される変換

だ．おい何かを説明するために別の何かを用意するな．今日は二次元回転がSO(2)で表せることを見て終わりたい．実はSO(2)の定義を日本語に直したのが先の回転の定義なのだ．

ここからは紹介になるから，話半分に聞いてほしい．

SOとはSpecial Orthogonal のことで日本語にするなら特殊直交であろう．これは変換を表現する行列が直交行列で行列式が1のものであると言うことなのだが，まぁ具体例を見て体験しよう．

二次元のベクトルを変換するものは二次元の行列だ．その中で直交行列とは転置行列が自身の逆行列，つまり行と列，縦と横を入れ替えて掛け算すると"1"になる行列だ．

具体的には例えば

おぉ確かに"1"になっている．これはちなみに45度回転の変換に対応している．

なぜこれが回転を表すかといえば，直交行列によって変換されたベクトルはその長さや内積を変えないからだ．

ベクトル"v"と"u"が変換行列"U"によって変換される時，その内積は上の式のようになって，元の内積に等しくなる．つまり直交行列によって"長さが変わらない"と言う回転の定義がそのまま反映されているのだ．

実は二次元回転は1つのパラメタで行列を表現できる．その表現は三角関数を使ってかける．

この時もパラメタ"θ"が回転の角度を表すことになる．

ちなみにこの変換はちょびっと変化の積み重ねでできる．長さ"1"の棒をちょびっとの角度"δ"だけ回転させた時，

のような変換になる．原理的には有限の角度もこのちょびっと変化を繰り返して移れるのだ．

後半はほとんど紹介になってしまった．今日話したことは，

・回転とは長さを変えない変換
・数学の言葉ではSO(n)群と結びつく
・SO(n)群は回転の変換そのものの定義を反映した変換を表す
・"何も変えない"からのちょびっと変化を生み出すものがある

だろうか．今日は前半だけふ〜んと聞いてもらえればいい．