
変わらない曲がり:一般相対論/曲率
前回までのあらすじをまとめておこう.重力の効果とは,座標変換で全て吸収できるという原理を受け入れると,時空が曲がることがわかった.曲がった時空を記述するために,時空の各点に物差し:計量gとちょびっと隣との曲がり具合:接続Γを導入したのだった.
今回は誰から見ても変わらない(観測者に依らない/座標不変)曲がり具合を導入したい.
ちょっと待て,前回導入した接続Γとは,ちょびっと隣との曲がり具合ではなかったのか?残念ながら,接続とは座標に依る,つまり見る人に依る曲がり具合なのだ.
簡単(で屁理屈的)な説明として,共変微分を使って座標によることを示せる.

共変微分∇はベクトルである.これは共変微分がベクトル(見る人に依らない)になるように決めたのだから当然だ.他方,偏微分∂はベクトルでない.共変微分を作らなければならない理由だった.共変微分は偏微分と接続で作られる.接続がテンソル(ベクトルのすごいの)であれば,ベクトルでないものとテンソルを合わせるとベクトルになってしまう.なので接続がテンソルではあり得ない....わかんない.
もうちょっと直感的な説明を試みよう.接続とはちょびっと隣との曲がり具合だった.そうちょびっと隣なのだ.その隣は"どこ"かを指定するために,人間には座標が必要になってしまう.これがダメな理由だ.

絵でいえば,赤から移そうと思ったとき,平行移動した時の緑の効果を青に載せるのが接続の役割だった.では赤の根元から青緑の根元に移す時,二点の場所を指定するために座標が必要になる.座標とは見るひとそのもの(の物差しの分布)だったから,結局接続が見る人に依っていることになる.残念.
でもどれぐらい曲がっているかというのは,曲がった世界では特徴的な量だろう.なんとしてでも,見る人に依らない量にしたい.どうしようか,ちょびっと隣の情報を,自分の場所だけで取り入れる必要がある.なんだかトンチのような問題だ.
実は簡単だ.行って帰ってこればいい.行ってしまえばちょびっと隣の情報を拾えるし,帰ってこれば自分の場所だけの話に戻ってくる.実際にやってみよう.
ボールと割り箸を用意してどこかにちょっと触れてほしい.平行移動を4回繰り返して元に戻ってくるとちょっと向きが変わっている.下の絵は,赤>緑>青>黄>紫と平行移動を繰り返した.赤と紫は同じ位置にいるのだが,向きが変わっている.これが時空が歪んでいる影響だ.

向きが変わるのはにわかには信じられないと思うので,ちょっと自分でやって見てほしい.後の話のために四点の絵を描いているが,三点でもいい.二点はだめだ.三点でおすすめなのは地球儀の赤道から北極へ,90°曲がってまた赤道に,そして出発点に帰って見てほしい.どうなるかぜひやって見てくれ(実際にやってコメントで答えを書いて見てほしい(コメコジキ)).ともあれこれで曲がりの情報を自分の場所だけで表せる.
ではこれを物理で使う数式の言葉で書こうと思う.さっきの絵を流用しよう.
矢印はベクトルだったから,ベクトルAを青>黄>紫と青>緑>赤と平行移動していこう.


各点の矢印は,前の矢印から平行移動でできてますよ〜と言う関係.最後の二行は,経路のちょびっと変化は同じだと言うことを示している.では紫と赤の差を考えてみよう.

最後の一行がポイントだ.そう,二階の共変微分の差になっている.これから,経路dxとベクトルの成分に依らない情報を取り出そうと思う.次のようなものが考えられる.

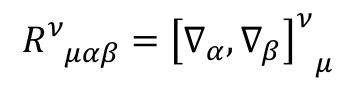
オシャレに交換関係を使って書いている.このRを曲率テンソルと言う.曲率と言うのはさっき見た曲がり具合を表しているのだ.
この曲率テンソルは共変微分から作られる.だからこれはテンソルなのだ.何が言いたいかといえば,これは見る人に依らない量なのだ.
次回はついに,ついにこれを使って物理法則を決めようと思う.聞いたことがあるかもしれないアインシュタイン方程式と言うものだ.
最後まで読んでいただきありがとうございます. 見ていただくだけでなく,"スキ",コメント励みになります. サポートいただければとても助かります/noblesse oblige(煽り)
