見るひとによってはいけない

物理の世界には相対論と呼ばれる理論がある．それを話したいがためにそもそも必要な"物理に於ける相対"の導入．

では始めよう．

物理の世界の"相対"の意味は"物理的に起こっている事実は観測者に依らない"と言う意味だ．は？

前後左右の相対

例えば車が走っている．

青い人曰く"車が右から左に走っている"，赤い人曰く"車が左から右に走っている"．観測者によって状況が違って見える．でも車は一台しか走っていない．走る方向も一方向だ．赤と青の人は同じものを見てるはずだ，これをどうしようか．

この世には同じ事実でも全く異なる言い方表現がある．それは赤青の立場(視点)の違いに依るものだろう．赤青それぞれに真実がある．立場の違いを認識せずにあたかも事実の認識が間違っているように争う人がいる．真実はいくつもあるが事実は一つだ．

閑話休題．赤青それぞれの人は真実を語ってる．とて互いに事実は一つだと知っている．これが物理に於ける相対論の出発点だ．物理法則は見る人に依る真実であってはいけない．物理法則は見る人に依らない事実を記述するものだ．

この状況について事実は"車が走っている"だ．方向については互いの方角を共有して話を進めなければならない．物理の世界の方角は"座標"と呼ばれる．青い人の右左前後(方角~座標)と赤い人の前後左右をすり合わせなければならない．赤の前後左右をひっくり返して後前右左にすれば青い人の前後左右になる．この視点の切り替えを物理の世界では座標変換と言う．

まとめ
・観測者によって見え方が違う
・物理的に起こっていることは観測者に依らない
・物理法則は観測者に依らないように書かれなければならない
・異なる観測者の見かた(座標)をつなげるのが座標変換

今日はここまでで終わってもいい．あとは具体例だ．

相対性の具体例

物理法則は観測者に依らないといった．ではどう言う形で表せば良いか，観測者はそれぞれ視点(座標)を持っているわけだから，物理法則を座標に依らないように書けばいいのだ．

実はもう座標に依らないように物理法則を書いている．それは運動方程式(であったり，作用)と言うものだ．

運動方程式は座標"x"とその時間微分"\dot{x}(xのドットつき)"によって書かれている．運動方程式を導く手順が上の画像なのだが，この処方箋が座標に依らなければいいのだ．

では具体例を見てみよう．外の赤い人がみる車と，赤い人から見て速度"v"で走る車の中の青い人を考えよう．

重力はかからないから作用はそれぞれこうなる．

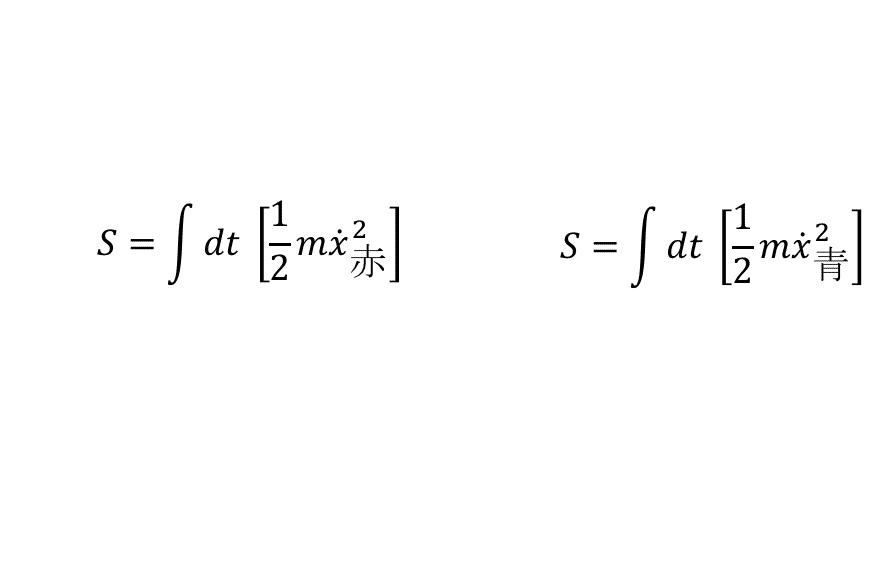
一緒じゃん．赤と青の座標"x_赤"と"x_青"の違いはあるが全く一緒だ．これから出てくる運動方程式も全く一緒に書かれている．

おぉ，これが座標に依らないと言うことだ．ここで言えるのは，この作用で書かれる理論は等速で走っている速度に依らない理論なのだ．例えばもっと別の速度で走る黄色い人がいても同じように運動方程式が書かれるはずだ．

赤と青の違いは微分方程式の解に必要な"境界条件"と言うのに現れる(微分方程式は解いて見せたことはないが)．

ちなみに赤と青の座標変換は

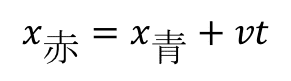
これの関係で赤い人と青い人の視点(座標)が繋がる．

touya_Y のお話物理｜touya｜note