ちょびっと変化:量子力学:運動量演算子

前回は演算子を使って調和振動子の固有状態とそのエネルギー固有値を出して見せたのだった．

今回は波動関数での表示を演算子から出してみよう．

波動関数とは状態と位置固有状態の内積なのだった．

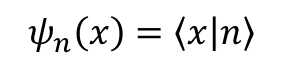
波動関数の二乗はその位置に粒子を見出す確率だった．これは状態"|n>"の時位置"x"に粒子を見出す確率を

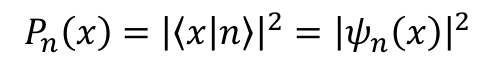
と決めたことと対応している．

ハミルトニアンを演算子でかいた時は運動量演算子で書かれていた部分

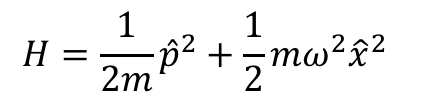
が波動関数の固有値方程式として書いた時は微分になっていた．

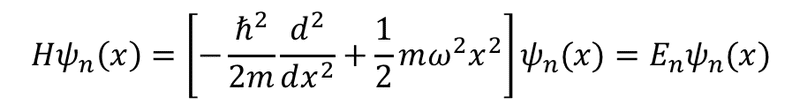
これをじっと見ると次のような対応があるように見える．

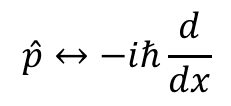
負号はどうやって出てきたんだよというのはさておき，運動量と微分が対応しているように見える．これを理解するのが今日の目標だ．

位置固有状態"|x>"とちょびっと変化させた位置固有状態"|x+ε>"を考えよう．"ε"は本当にちょびっとの数字とイメージして欲しい．これに位置演算子を作用させれば当然

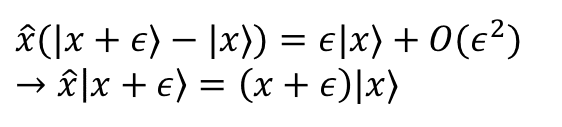
位置の固有値が帰ってくる．この時ちょびっとの量"ε"はものすごく小さい数だから"ε^2"はカスみたいに小さいと思って無視しよう．そうすれば位置固有状態"|x+ε>"はほとんど"|x>"と思っていいという感じだ．

他方交換関係に位置固有状態を作用させてみよう．

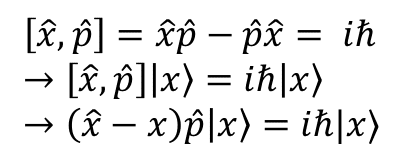
矢印の最後をじっとみれば，"p|x>"に位置演算子を作用させたものと元の状態の差が書かれているように見えてくる．

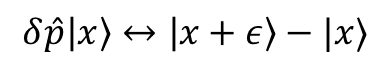
"δ"はちょびっと量だ．この"δ"は"ε"とどんな関係にあるかといえば

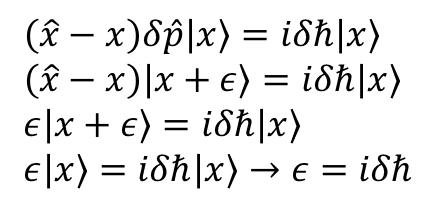
となっている．ここまで用意して，波動関数を見てみよう．

波動関数のちょびっと変化から考えると

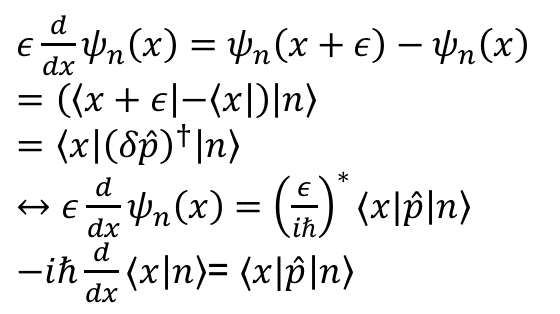
と確かに運動量演算子と微分が結びついた．

今日は数式を雰囲気でいじり回していたが，この話のキモは

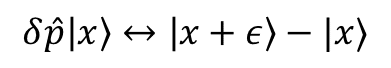
とおいたことだった．これの意味するところは，運動量演算子を作用させると位置固有状態の固有値がちょびっと進むということだ．

これを物理っぽくいうと"運動量演算子は位置並進の生成元"と言う．