天下り導出:特殊相対論/電磁気は相対論的

今回は特殊相対論からみた電磁気の話をしようと思う．本来はゲージ理論と(ふんわり)微分幾何(びぶんきか)の視点から見ればやっていることは超簡単なのだが，今日は天下り的に操作を追っていこうと思う．

はじめに

電磁気の法則は今までの(ガリレイ)変換ではうまく行かなかった．

で見たように電磁気の法則はガリレイ変換では見る人によって法則が変わる，物理の信条からは外れたものだった．

今回は電磁気の法則(運動方程式)が特殊相対論的な手続きで出てくることを見よう．今回の説明では天下り的に見えるが，実はそれは別の見方をすれば筋が通っている．またいつか話そうと思う．

謎のベクトル"A_μ"，テンソル"F_μν"

謎のベクトル"A_μ"を用意する．これをなぜかベクトルポテンシャルと呼ぼう．ベクトルの形のポテンシャルなのだ．ポテンシャルと言うからには，これを使って何かを引き出すのだ．

ベクトルポテンシャルから引き出すものは電磁場テンソル"F_μν"と言う．

"∂"とは微分のようなもので0~3まで数字が走ると，それぞれt,x,y,zで(偏)微分しろと言う意味になる．

"F_μν"は添字の入れ替えで符号が反転する．"F_μν"の決め方からも反対称なのがわかると思う．

"F_μν"の中に電場と磁場がある．電場"E"と磁場"B"は

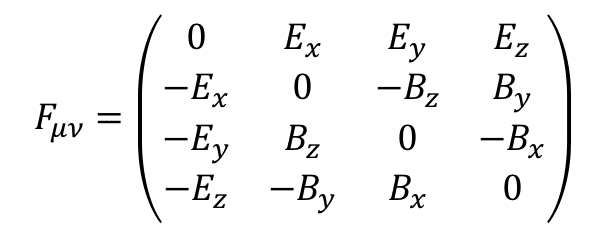
のように中に入っている．添字の入れ替えは縦横をひっくり返すことに対応するので，ここからも"F_μν"が反対称なのがわかると思う．

運動方程式

とりあえず"F_μν"を決めたのでそこから運動方程式を考えよう．

まずは"F_μν"の定義から自動的に満たされる式(Bianch(ビアンキ)恒等式)

と，物理の要請から出てくる湧き出しの式．

"j^ν"は0成分が電荷，1,2,3成分が電流を表すものだ．電流と関係することで数学から物理になる(イメージ)．

この二つを持って電磁気の運動方程式になる．各成分を見ていくと

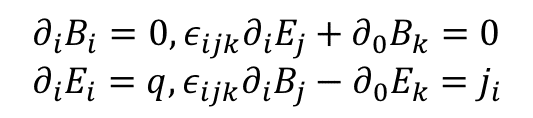
となる．ちなみに

このお話物理では陽に言っていないが，これがもともとあった電磁場の運動方程式なのだ．Maxwell(マクスウェル)方程式と名前が付いている．

何が嬉しいかといえば，相対論的なテンソル微分方程式が実はもともとあった電磁気の運動方程式になっているのだ．これから言えるのは電磁場は実はすでに相対論的なものだったのだ．

まとめ

・相対論的なテンソルを構築して，その成分を電場"E"と磁場"B"と呼ぶことにした
・物理の要請と数学的な恒等式から微分方程式を作った
・作った微分方程式が実は電磁場の運動方程式になっていた

つまるところ，電磁気はもともと相対論的なもので，ガリレイ変換でおかしく見えたのは電磁気が間違っているのではなく，ものの見方，相対性が間違っていたのだ．

touya_Y のお話物理｜touya｜note