歪んだ物差し:一般相対論/計量
前回は,重力の影響は相対性原理から空間の歪みに置き換えられることを見た.
そこで立場を変えよう.重力とは,物体間の力ではなく,物体が時空と影響を与え合う現象のことを言うと.

時空の歪みが重力の本質になると言う立場だ.
何が嬉しいかといえば,二つの物体を用意して初めて重力の話を始められたのに対して,一個物体をおけば重力(時空)の話ができるのだ.二つ目の物体は物体同士ではなくまた時空と相互作用する.もう一歩踏み込めば,離れた場所の情報がいらなくなるのだ.時空の歪みは物体から決められて,物体はその一点の空間の歪みがわかれば重力の情報がわかる.手元の情報だけでやりたいことができるのだ.
ではどうやって時空の歪みを記述しようか.実はここで計量が出てくる.計量とは長さの決め方を指定する物差しのようなものだった.歪んだ物差しがあれば歪んだ空間の歪みを書ける.
特殊相対論の時は時空の全てに渡って同じ計量"η"を使っていたが,一般相対論では時空の各点各点に計量"g(x)"が決められている.歪み方は時空の各点各点できっと違うから,それを記述するために"g(x)"も各点に必要なのだ.
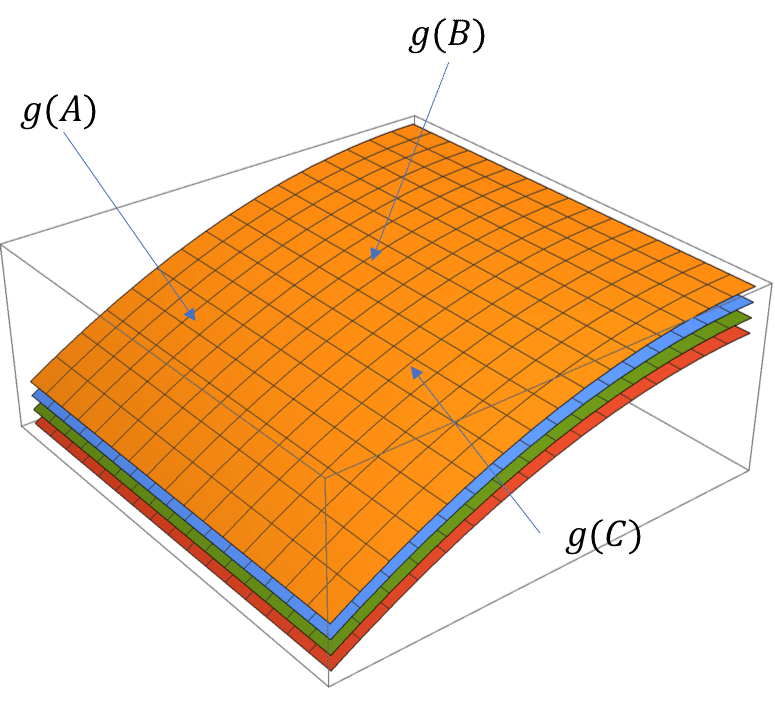
もちろん,全く重力の影響が無い空間は特殊相対論的な時空になる.その時は全ての時空の各点の計量が"g(x)=η"になる.
重力の影響は時空の各点各点の計量で決められる.
次回からは少し数学の作業になると思う.計量からどうやって重力の影響を取り出すかを考えていこう.
何か質問があれば気軽にコメントをしてほしい.どんな素朴な疑問でもきっと答える価値のあるものだと思う.
最後まで読んでいただきありがとうございます. 見ていただくだけでなく,"スキ",コメント励みになります. サポートいただければとても助かります/noblesse oblige(煽り)
