新・透明駒源泉館（解答編　その1）

表記法など細かいルールについては「透明駒をはじめから」を参照のこと。尚、判明した透明駒については、詰め上がりにおいて枡目に色をつけている。

　　　　　　　　　　　(1)

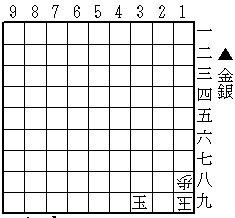
　　　　　　　　　　　ばか詰　3手（透明駒0+1）

29金、同X、28銀（X=角）迄3手詰。

　　　　　　　　　　　（詰め上がり）

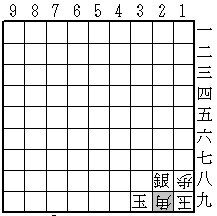
29金を取らせておいて28銀と打つことで、29にある透明駒が先手玉に王手をかけていないこと、即ち2手目が同角生だったことが証明される。
　言う迄もないが、これは詰パラ9月号の「透明駒入門発刊記念作品展」の元ネタである。流石にこれだと考えるところがないかと思って、先手にも透明駒を持たせてかしこにしたのだが、今度は詰め上がり形が定まらないことで不安を感じた解答者が多かったようだ。

　　　　　　　　　　　(2)

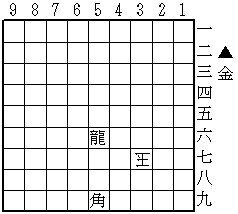
　　　　　　　　　　　ばか詰　3手（透明駒1+0）

　X、36玉（X=香）、26金迄3手詰。

　　　　　　　　　　　（詰め上がり）

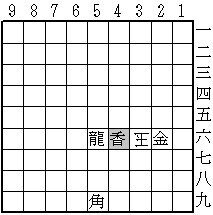
　初形で既に王手がかかっていると現在先手番ということと矛盾するので、透明駒が48にいることは明らか。これが動いて王手を掛け、2手目に玉が36に動けたのだから、初手は48香が46に動いたことになる。
　ここでは動いた駒が透明飛ではないことを36玉によって証明しているのだが、この例から分かるように、同じ動きができる透明駒が数種類あるとき、一般的には弱い駒の方が証明が容易い。では逆に、「48から46へ透明飛が動いた」ということは、どういう構図なら証明できるだろうか。一寸考えてみて下さい。

　　　　　　　　　　　(3)

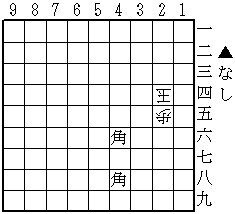
　　　　　　　　　　　ばか詰　3手（透明駒1+0）

X、15玉（X=37飛）、17飛迄3手詰。

　　　　　　　　　　　（詰め上がり）

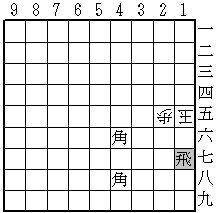
　2手目に15玉と動けることから、初手は35の透明駒が48の角の利きを止めるように動いたことになる。そのような動きができるのは飛しかないから、2手目を指し終えた時点で37に飛が可視化し、3手目が指せることになる。
（2）では「弱い駒の方が証明しやすい」と書いたが、それは同じ利きを持つ駒が複数ある場合であって、ある動きができる駒が1種類しかない場合には、すんなり透明駒の駒種が判明することになる。

　　　　　　　　　　　(4)

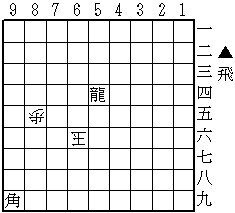
　　　　　　　　　　　ばか詰　3手（透明駒1+0）

96飛、75玉、X(=76歩)迄3手詰。

　　　　　　　　　　　（詰め上がり）

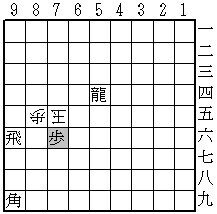
　これも初形で88か77に透明駒が挟まっていることは明らか。初手96飛と打ち、75玉にXとすると、飛が売り切れの為、75玉に王手を掛けられる透明駒は77歩しかない！
　最終的に透明駒が歩だと判明する作品はかなり珍しく、「透明駒入門」の中にもそのような作は1作もないようだ。もっとも、最後まで正体が確定しないまま詰め上がる作品も多く、その方がより高度だという意見もあるので、特にスゴいことをやっている訳ではない。

　　　　　　　　　　　(5)

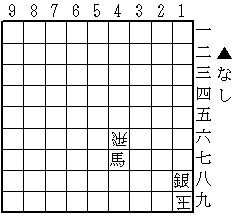
　　　　　　　　　　　ばか詰　3手（透明駒0+1）

37馬、28飛、X（=金）迄3手詰。

　　　　　　　　　　　（詰め上がり）

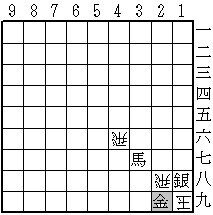
　3手目にXと指すことで、初手が透明駒を取る手だったことが証明される。そして、2手目に飛を売り切れにしておけば、3手目は29金打の可能性しかなく、これで詰を主張できるという訳。
　透明金は、その利きのみでは証明が難しい（龍・馬も同じ動きができるし、何より小駒成駒と区別がつかない）。なので本作では、「持駒にしてから打つ」という手順構成にしてある。では、持駒を経由せずに透明金を証明する方法はあるだろうか？例えばこういうところに、透明駒創作のきっかけが転がっている。

（明日へ続く）