透明駒をはじめから（2）

　　　　　　　　　　　例2 

ばか詰　3手（透明駒 1+0）

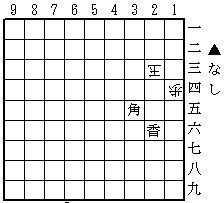
　初形で王手がかかっていると、現在先手番であることに矛盾するので、攻方の透明駒は24、25のどちらかにあります。では、どちらにあって、その種類は何なのでしょう？
　まず、X、13玉！と進めてみましょう。2手目に13玉と指せる為には、24に攻方の透明駒が配置されなければならず、しかもその透明駒は13への利きを持っていてはいけません。従って、それは歩、香、桂、飛のいずれかです。このうち、初手に25から24へ動いても合法な駒は歩しかありませんね。つまり、初手Ｘは、25歩を24に突き出す手だったということが「証明」されました。2手目13玉と指した時点で透明駒の位置と種類は完全に確定しましたから、24歩は可視化され（→仮定(3)）、3手目23歩成とすることができます。

　ここで「証明」という言葉を使いましたが、これは数学でいう証明とは意味が異なります。透明駒における「証明」は、「もしそうでなければ、手順が合理的に説明できない」という意味で用いられます。例3では、Ｘ、13玉という2手が合法である為には、2手目に24歩がいなければなりませんでした。つまり、この2手によって「現在先手の透明駒が24にいて、それは歩である」ということが「証明」されたのです。
　これこそ、透明駒特有のロジックです。普通の詰将棋なら、配置がまずあって、それらを動かすことで手順が生じます。ところが透明駒では、逆に手順が先にあって、それが配置を規定するのです！この論理の倒錯が、透明駒を取っつきにくいものにしていると同時に奥深いものにしていると、個人的には思っています。

　　　　　　　　　　　例3 

ばか詰　5手（透明駒 0+2）

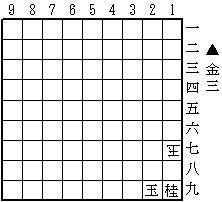
まずは18金、18Xとしてみましょう。この時点で1枚後手の透明駒が18にいることは確かですね。続いて28金と指せば、18に飛が浮かび上がってきます。何故なら、この3手目が合法ということは、18金を取った透明駒が先手玉に王手をかけていなかったことを意味するからです！
　3手目28金も同様に28Xと取ってもらい、最後に27金と打てば、全く同様の意味付けで28に生角があることが示され、これで確かに後手玉は詰んでいます。
　尚、透明飛は38～98のいずれかにいた訳ですから、28金、同X、18金の順では飛が18に入れず失敗します。

　　　　　　　　　　　例4 

ばか詰　3手（透明駒 1+1）

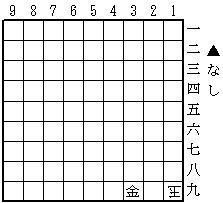
　初手は28金とします。これが王手であることから、49～99のいずれかに攻方の透明飛（又は龍）がいることが分かりますね。玉方の2手目は29飛！です（意味は後述）。これを同金と取ってしまうと、今度は玉方にも透明駒があるので、29Xと取り返されてしまいます。3手目はX！で、これで詰。意味が分かりますか？
「そもそも、攻方には1枚しか透明駒がなかった筈では？」という声が聞こえてきそうですが、これでいいのです。攻方の透明飛（龍）では3手目に王手をかけることができないのに、3手目も透明駒の着手だという、一見ありえない手順。これを合理的に説明する手段が1つだけあります。つまり、初手28金は玉方透明駒を取る手だったのです！
　だとすれば、3手目はその取った透明駒を打つ手ということになり、これが王手であることから18に透明金が浮かび上がります（→仮定(2)）。納得して頂けましたか？
　ここでも、手順限定の論理は「3手目に打てた」→「だから初手は駒取りだったのだ」というように、逆立ちしていますね。言い換えると、3手目の着手によって初手の駒取りを「証明」したことになります。
　尚、2手目飛合限定なのは、飛を売り切れにする意味です。他合では、4手目18歩などとして「透明飛による王手だった」と主張されてしまいます。又、29以外だと、4手目に29飛とされ「3手目は29透明金だった」ということにされてしまいます。