超簡単　比例　（小学算数）

6年生で習う比例は、実は中学校以降の勉強の基礎になる重要な単元です。数学だけではなくて、例えば中学理科の応用問題は、ほとんど比例を使って解きます。

基本をしっかりと理解しよう

他の単元とちがって、比例では大事なことを最初にしっかりと理解しておかないといけません。覚えておかないといけないことはたった4つです。

比例とは

長さ1mで重さが10gの針金があるとします。2mだと20g、3mだと30g、…と、長さが増えたら重さも同じように増えていきます。
これが比例です。

増え方にも規則があって、長さが1m,2m,3m,4m,…と2倍,3倍,4倍…になると、重さも10g,20g,30g,40g,…と2倍,3倍,4倍…になっています。

比例の式

次に、比例や反比例では、いろいろな値をとる片方をx、もう片方をyで表します。この例だと、長さ（m）がx、重さ（g）がyです。

もう一度、表を見てください。

表の下（重さ、y）はいつも、上（長さ、x）の10倍になっています。
このとき、式はy=10×xだ、といいます。

10と数字を入れたところは問題によっていろいろ変わるので、
比例の式は、y=きまった数×x
と覚えます。

比例のグラフ

次に、比例の関係にある2つの数はグラフに表すことができます。

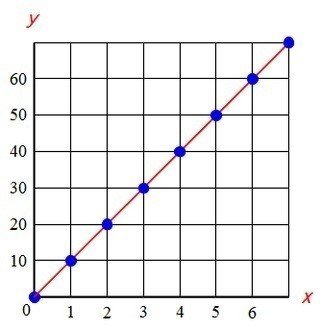
横の軸でxの値を見つけ、縦の軸でyの値を見つけて、
x=0のときy=0、
x=1のときy=10、
x=2のときy=20、
…というふうに点を打っていって、
最後にすべての点を通る直線を引きます。

0から始まってグラフの端まで直線を引くことになります。
このことを、比例のグラフは0を通る直線であるといいます。

比例の文章題

最後に、比例の文章題の解き方を考えます。
「長さ2mのとき重さが8gの針金があります。この針金3mの重さは何gですか。」これが比例の文章題です。

長さ2mで重さは8gなので、針金1mの重さは8÷2=4gです。
1mが4gの針金が3mあるので、答えは4×3=12gです。

つまり、まずわって1mにあたる量を求めて、次にかけて答えを求めたらよいのです。

比例で知っておかないといけないこと

以上より、比例で覚えておかないといけないこと4つは次のようになります。

1、比例では、片方が2倍,3倍,4倍…になると、もう片方も2倍,3倍,4倍…になる。

2、比例の式は、いつもy=きまった数×xで表すことができる（「きまった数」を求めると比例の式が完成します）。

3、比例のグラフは、0を通る直線になる。

4、比例の文章題は、わって1にあたる量を求めて、かけて答えを出す。

では、覚えられたかどうか、例題で試してみましょう。

例題：次の表は、リボンの長さxmと代金y円の関係を表しています。

（１）yはxに比例しますか。
（２）yをxを使った式で表しなさい。
（３）xが9のときyの値を求めなさい。
（４）yが850のときxの値を求めなさい。
（５）xとyの関係を表すグラフをかきなさい。
（６）長さ3mで代金が120円の別のリボンがありました。このリボンを5m買うと代金はいくらになりますか。

（解答）
（１）yはxに比例しますか。
片方が2倍,3倍,4倍…になると、もう片方も2倍,3倍,4倍…になれば比例です。
xが1,2,3,4,…と2倍、3倍、4倍になると、yも50,100,150,200,…と2倍、3倍、4倍になっているので、比例しています。

（２）yをxを使った式で表しなさい。
表の下はいつも上の数値の50倍になっています（50÷1=50、100÷2=50、150÷3=50、…になっています）。
比例の式y=きまった数×xの「きまった数」が50だから、
y=50×xです。

（３）xが9のときyの値を求めなさい。
yはいつもxの50倍なので、9×50=450です。
または、y=50×xの式でx=9だから、y=50×9=450です。

（４）yが850のときxの値を求めなさい。
yはいつもxの50倍なので、850÷50=17です。
または、y=50×xの式でy=850だから、50×x=850より、x=850÷50=17です。

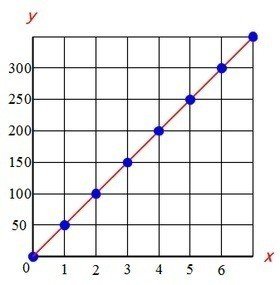
（５）xとyの関係を表すグラフをかきなさい。
比例のグラフは、0を通る直線になります。

（６）長さ3mで代金が120円の別のリボンがありました。このリボンを5m買うと代金はいくらになりますか。
比例の文章題は、わって1にあたる量を求めて、かけて答えを出します。
120÷3=40
1mの代金が40円だから5mの代金は、
40×5=200円です。