
【ここまで気にしてる?】正弦定理で大活躍する円周角の定理をご存知ですか??
こんにちは。とまねぎです。
今回の記事では、↓の記事
こちらで大活躍する
「円周角の定理」の復習をします。
「円周角の定理」は
中学校3年生で学習します。
その便利さから高校でも重宝され、
図形を分析するために大活躍する定理です。
分かりやすい定理なので
「余裕だぜ!!」と思っている方も
居らっしゃるかもしれません。
…本当に?
意外と盲点な内容もありますよ?
本当に全部理解していますか??
しかも、円周角の定理は
数学Ⅱに繋がる重要な話が絡んでいます。
それにも気付いていますか??
「えっ…??」
と感じた方は最後まで読んでください。
そんな奥が深い円周角の定理ですが、
本記事を読むことで
次のような学習効果が期待できます。
・円周角の定理の基本を全て復習することができる。
・数学Ⅱに関連する話を確認することができる。
それでは、始めましょう。
意外と奥が深い円周角の定理
1.円周角の定理の基本
まず、用語の確認からいきましょう。

ざっくり解説します。
円周角は
「弧の両端から伸びた2直線により
円周上に作られる角」
で、
中心角は
「弧の両端から伸びた2本の
半径により中心に作られる角」
です。
まあ、そのままですね。
この円周角には
次のような性質が成り立ちます。

「同じ弧に対する円周角は等しい」
という特徴で、
画像の5つの図形に書かれている
∠APBは全て同じ角度になります。
また、↓のような特徴もあります。

簡単にいってしまうと、
「円周角は中心角の半分になる」
という特徴です。
これも重要な特徴なので
頭に叩き込んでおきましょう。
ここでは3パターンに分けて
「円周角は中心角の半分になる」
具体例を紹介してあります。
各図を拡大したものがこちらです。
赤い角度が円周角で、
青い角度が中心角です。
参考としてザックリ解説しますが、
「円周角は中心角の半分になる」
という認識がもてればそれでOKです。
読み飛ばしてくれても構いません。

まずはこちら。
半径が等しいのでOP=OBとなります。
これにより△OPBが
二等辺三角形であると分かるので、
∠OPB=∠OBPという特徴を
上手く利用するとよいです。
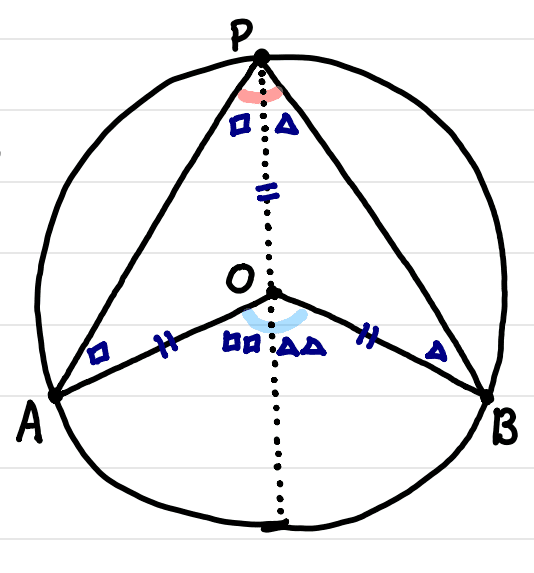
続いてこちら。
∠APBを直線OPで分けて
▢,△としておきます。
このとき、直線OPは
∠APBを二等分している
わけではないことに注意しましょう。

最後はこちら。
これは難しいですね。

まずは細長い三角形に注目です。
この三角形は2つの辺が半径なので
二等辺三角形になります。
なので、青▲の角度が等しいです。

すると、真ん中赤〇の角度が
青▲2つ分であることが分かります。

続いて右側に見つかる
三角形に注目です。
この三角形もまた
2つの辺が半径なので、
二等辺三角形になります。
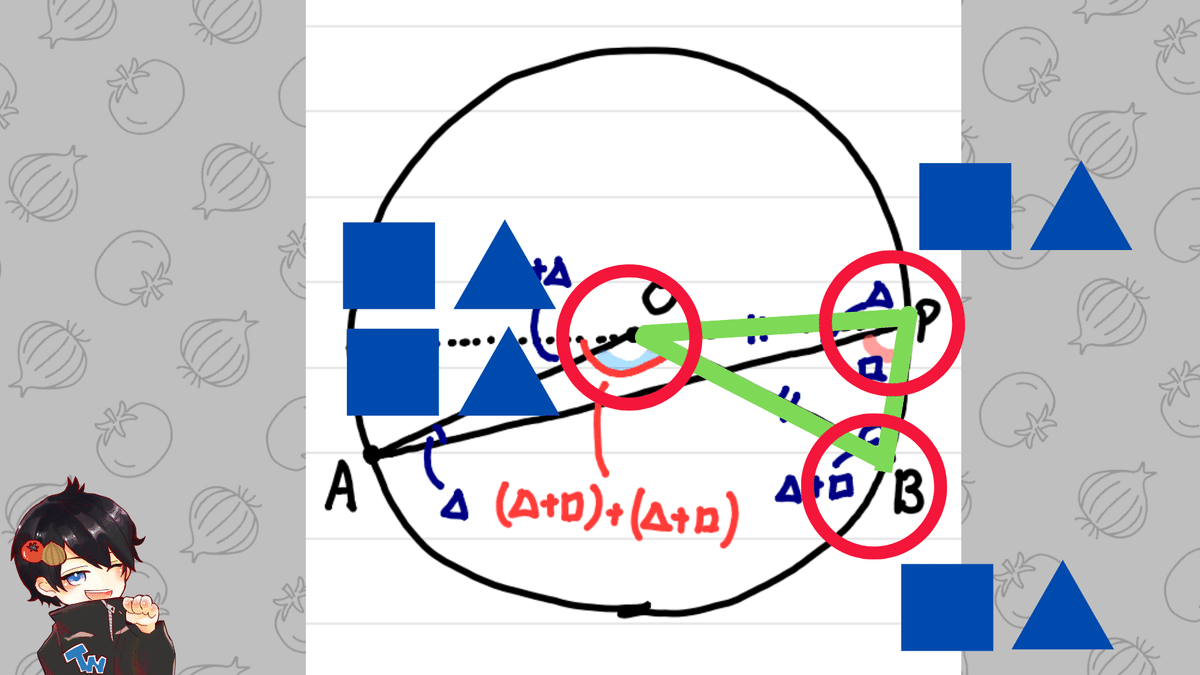
すると、中央の赤〇の部分の角度が
青■2つ分と青▲2つ分になることが分かります。

あとは大きい緑〇から
小さい緑〇を引いて、
∠AOBが青■2つ分と求まり、
やっぱり円周角は中心角の
半分になっていることが分かります。
改めて、
円周角の定理とは何か
まとめておきましょう。
まずは超基本的なことです↓

続いて、円周角と中心角について↓

円周角が分かれば中心角が分かるし
中心角が分かれば円周角が分かる。
この関係は大切です。
忘れがちなのは
中心角が180°のとき、
円周角が90°になるということです。
そしてこのとき、
弦ABは直径と一致します。
この知識は正弦定理でも活用するので
絶対頭に入れておきましょう。
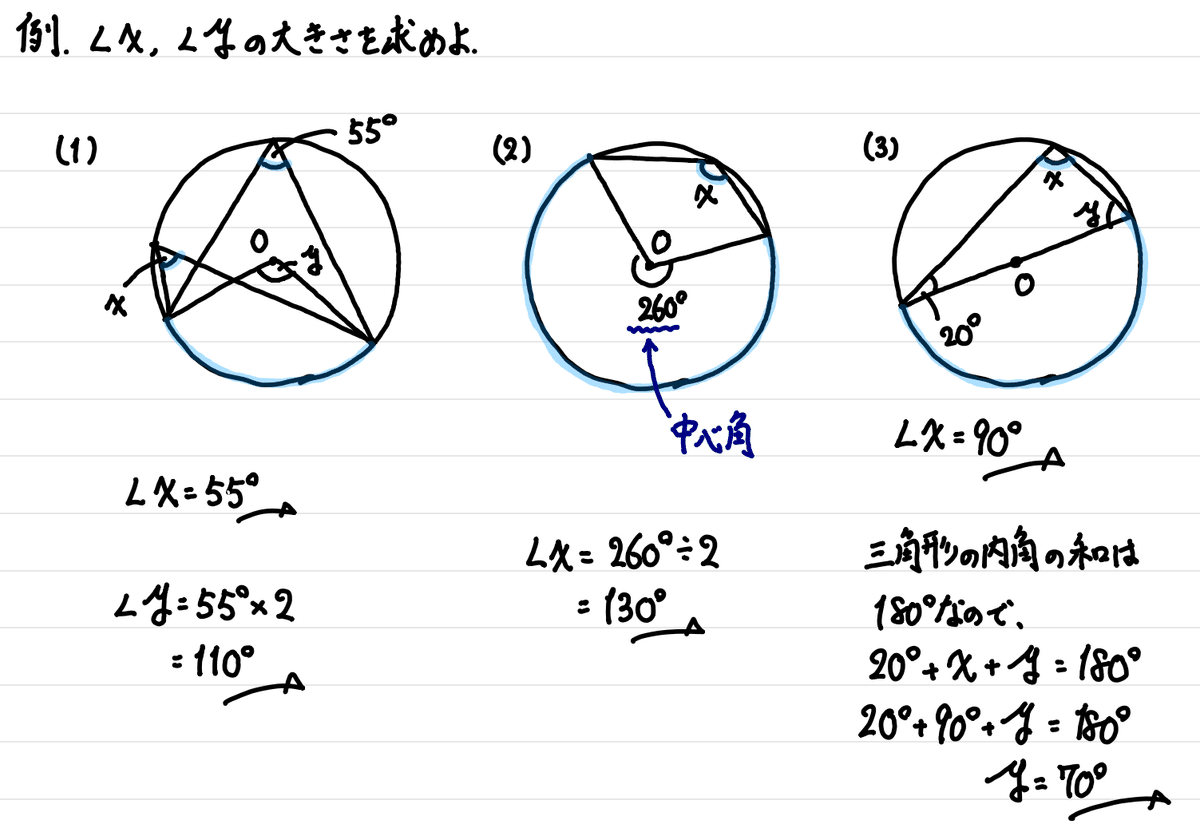
一応問題も用意したので、
参考にしてください。

解説です↓
2.円周角の定理を進化させる
これまで見てきた円周角の定理は、
実は進化します。
まずは結論からどうぞ。

「同じ円の中では、
弧の長さが等しいと円周角も等しい。」
こんな特徴があります。
なんと、
同じ弧の円周角が等しいだけでなく、
違う弧でも長さが等しければ
円周角は等しくなるのです。
これは忘れている高校生も
いるのではないでしょうか?
ちなみに、この話は中心角についても
同じことが言えます。

中心角が等しかったら弧の長さが等しいし、
弧の長さが等しければ中心角が等しい。
こんな特徴もあるんですね。
弧の長さと角度には
強いつながりがある。
この認識をもってください。
後の話で重要になってきます。
参考までに、
弧の長さが等しければ
円周角が等しくなることの
証明を載せておきます。
できなくても良いです。
「へーー」くらいの
気楽な感じでいきましょう。

3.数学Ⅱと関連する重要な話
高校生の皆さんが気になるのは
ここからの話かもしれません。
項目2で紹介した
弧の長さと円周角の関係から
次のようなことが言えます。

要するに、
弧の長さが2倍になれば
円周角も2倍になる。
ということですね。
もちろん、
弧の長さが3倍になると
円周角も3倍になります。
当然、弧の長さが4倍になると
円周角も4倍になります。
こうした関係から、
「円周角は弧の長さに比例する」
と言えそうです。
実はこの関係、
中心角についても
同じことが言えます。
むしろ、中心角の方が
弧の長さと強い関係があるので、
「中心角は弧の長さに比例する」
と言った方が正しいかもしれません。

ここの話は少しややこしいので
図にまとめておきました。

図にも書いたように
中心角と弧の長さの関係が基本です。
中心角が大きくなればなるほど、
弧の長さも長くなります。
その中心角を半分にすると
円周角が求まるので、
結果的に円周角が大きくなると
弧の長さも長くなる…
ように見えているだけです。
さて、
中心角と弧の関係が分かったところで、
高校の数学に関係する話をします。
中心角と弧の長さは1対1に対応します。
例えば、中心角が1°だったら
その角度に対する
弧の長さが1cm…みたいな感じで
対応する長さがたった1つ存在します。
(実際に1cmではありません。)
これは2°でも3°でも同じです。
2°だったら弧の長さが○○
3°だったら△△…と言った感じで、
様々な角度(中心角)に対して
弧の長さが1つずつ決まっています。
これを言い換えると、
「角度は弧の長さを使って
表現することができる」
となります。
例えば、
弧の長さが1cmだったら
角度は1°だなー。
だから、1°を1cmと表現しよう!
2cmだったら2°だなー。
だから2°を2cmと表現しよう!
みたいな感じです。
(実際は1cmや2cmではありません)
つまり、
角度は弧の長さでも表現できる
というわけです。
これが高校でとても重要になります。
根本的な扇形の弧の長さについて
私たちが学習するのは小学校です。
小学校で学習したものが
高校で学習する重要な考え方の
基礎になっている。
算数・数学のつながりを感じます。
「何故わざわざ角度を
長さで表現する必要があるのですか?」
という質問については
「その方が便利だから」
という回答をすることになります。
その便利さは数学Ⅱで
詳しく語ることになるので、
しばらくお待ちください。
今回の話を通して知ってほしいこと。
それは
角度は弧の長さでも表現できる
これです。
参考までに、中心角と弦の間には
比例の関係はありません。
つまり、中心角が2倍になったからと言って
弦の長さが2倍になることはない。
ということです。
弧と弦、違いを明確にしておきましょう。

まとめ
最後に、円周角の定理のまとめです。

このまとめの図とは別に
「中心角が大きくなるほど
扇形の弧の長さも長くなる。」
という関係を使って
「角度を長さで考えることがある」
ということを覚えておきましょう。
それでは、この記事で学んだことを活かして
こちらの記事で正弦定理を学習してみてください↓
本日はここまでとします。
お相手はとまねぎでした。
この記事が気に入ったらサポートをしてみませんか?
