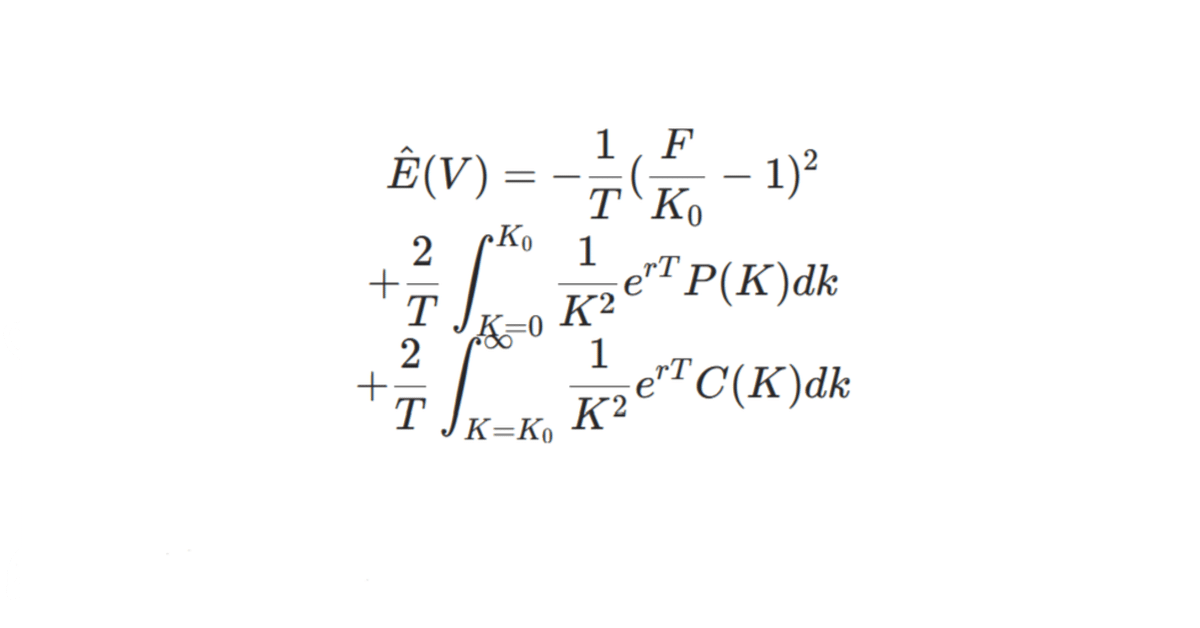
VIXを求める式の導出
VIXというのは、SP500の予想ボラ(Implied volatility)のインデックスです。オプション取引でなくてはならないパラメータですが、実際の計算はかなり複雑なものになっています。
Wikipedia(https://en.wikipedia.org/wiki/VIX)の記述では、過去には、VIXインデックスはいろいろな計算方法がなされていたようです。1993年にCBOE取引所が、市場のボラをRealtimeにリポートする「VIXインデックス」ができたました。当時は、SP500のATM(アットザマネー)オプションのImplied volatilityを計算しただけものだったようです。2003年から、ゴールドマンザックスとCBOEが今の計算方法を共同で確立し、今日にいたっています。
現在の計算方法は、CBOEのサイトに詳しく乗っています(https://cdn.cboe.com/api/global/us_indices/governance/Volatility_Index_Methodology_Cboe_Volatility_Index.pdf)。しかし式はかなり不思議な形になっています。以下の式のルートがVIXになるわと書かれているのです。
$$
\sigma^2 \approx
\frac{2}{T}\Sigma_i\frac{\Delta K_i}{K^2}e^{rT}Q(K_i)-\frac{1}{T}[\frac{F}{K_0}-1]
$$
Kがオプションのストライク価格、Sは株価、Fは同じ満期の先物価格(金利などを考慮した今の価格)、QがOTMコール、またはOTMプットの価格になります。どうしてこのような式になるのでしょう?直感的には、OTMオプションの価格分布はATMがピークでそこから下がる形になっており、予想ボラが大きければ広がり、予想ボラが小さければ狭まるので、その形から計算できるのはわかりますが、果たして本当でしょうか。今日は、この式の導出を試みようと思います。巻末にある文献をむっちゃ参考にしています。
Wiener確率過程モデルで株価のブラウン運動を考えましょう。Sが価格。σが値動きの分散、μはドリフト項です。dWはランダムノイズで、tが時間です。
$$
\frac{dS}{S} = \mu dt + \sigma dW
$$
伊藤公式から
$$
d\log{S} = \frac{1}{S}dS-\frac{1}{2}\frac{1}{S^2}(dS)^2\\
=(\mu dt + \sigma dW) - \frac{1}{2}(\mu dt + \sigma dW)^2\\
= (\mu-\frac{1}{2}\sigma^2)dt + \sigma dW
$$
$$
(dt)^2=0, (dW)^2=dt, dWdt=0 に注意
$$
上の2式を引き算して
$$
\frac{\sigma^2}{2}dt=\frac{dS}{S}-d\log{S}
$$
満期(T)までの積分をします。ここで株価の平均の分散Vを導入します。括弧内で文字の0は今の時間の値、Tは満期での値です。
$$
\frac{1}{2}VT =\int_0^T\frac{dS}{S} - \log{\frac{S(T)}{S(0)}}
$$
ちょっと変形して
$$
V = \frac{2}{T}\int_0^T\frac{dS}{S} - \frac{2}{T}\log\frac{S(T)}{S(0)}
$$
両辺の期待値を求めます。(Eは期待値、Fは現在の先物価格)
$$
\hat{E}(V) = \frac{2}{T}\log\frac{F}{S(0)} - \frac{2}{T}\hat{E}(\log\frac{S(T)}{S(0)})
\qquad (式1)
$$
これが最終的に求めたい、株価Sの分散の期待値、ということになります。
さて、次のような積分を解きます。OTMのプットオプションのみを考え、満期のときの株価格S(T)よりも、ストライク価格Kより大きい時だけK-S(T)を積分する形になります。つまり、K-S(T)は常にプラスになります。At the moneyに近いストライクをK0として考えましょう。
$$
\int_{K=0}^{K_0}\frac{1}{K^2}\max(K-S(T))dK
$$
これは結局以下のように書き換えられます。
$$
\int_{K=0}^{K_0}\frac{1}{K^2}\max(K-S(T))dK
$$
$$
\begin{cases}
=\int_{K=S(T)}^{K_0}\frac{1}{K^2} (K-S(T)) dK\\
\qquad =\int_{K=S(T)}^{K_0}\frac{1}{K}dK-\int_{K=S(T)}^{K_0}\frac{S(T)}{K^2}dK\\
\qquad =\log\frac{K_0}{S(T)}+\frac{S(T)}{K_0}-1
& \text{for} \quad K_0 > S(T) \\
=0 &\text{for} \quad K_0 < S(T)
\end{cases}
$$
同様にコール側も行います。
$$
\int_{K=K_0}^{\infty}\frac{1}{K^2}\max(S(T)-K, 0)dK
$$
$$
\begin{cases}
=\log\frac{K_0}{S(T)}+\frac{S(T)}{K_0}-1
&\text{for} \quad K_0 < S(T) \\
= 0 &\text{for} \quad K_0 > S(T)
\end{cases}
$$
コール側とプット側を足すと全区間のS(T)で次のようにあらわされます。
$$
\int_{K=0}^{K_0}\frac{1}{K^2}\max(K-S(T), 0)dK\\
+\int_{K=K_0}^{\infty}\frac{1}{K^2}\max(S(T)-K, 0)dK\\
=\log\frac{K_0}{S(T)}+\frac{S(T)}{K_0}-1
$$
ちょっとだけ変形します。
$$
\log\frac{S(T)}{K_0}=-\frac{S(T)}{K_0}+1\\
-\int_{K=0}^{K_0}\frac{1}{K^2}\max(K-S(T), 0)dK\\
-\int_{K=K_0}^{\infty}\frac{1}{K^2}\max(S(T)-K, 0)dK
$$
期待値を求めましょう。ここでコール価格C、プット価格Pを導入します。金利による影響も考慮してリスクフリー金利rを使います。
$$
\hat{E}(\log\frac{S(T)}{K_0}) = -\frac{F_0}{K_0}+1\\
-\int_{K=0}^{K_0}\frac{1}{K^2}e^{rT}P(K)dk\\
-\int_{K=K_0}^{\infty}\frac{1}{K^2}e^{rT}C(K)dk
\qquad (式2)
$$
ここで式1に戻るのですが、その前に第1式の第2項は次のようにも書き換えられます。
$$
\hat{E}(\log\frac{S(T)}{S(0)})
=\hat{E}(\log\frac{S(T)}{K_0}
+ \log\frac{K_0}{S(0)})\\
= \log\frac{K_0}{S(0)} +\hat{E}(\log\frac{S(T)}{K_0})
\qquad (式3)
$$
式1、2、3を組み合わせて
$$
\hat{E}(V) = \frac{2}{T}\log\frac{F}{S(0)} - \frac{2}{T}\hat{E}(\log\frac{S(T)}{S(0)}) \\
= \frac{2}{T}\log\frac{F}{S(0)}
- \frac{2}{T}\log\frac{K_0}{S(0)}
-\frac{2}{T}\hat{E}(\log\frac{S(T)}{K_0}) \\
= \frac{2}{T}\log\frac{F}{K_0}
-\frac{2}{T}[\frac{F}{K_0}-1]\\
+\frac{2}{T}\int_{K=0}^{K_0}\frac{1}{K^2}e^{rT}P(K)dk \\
+\frac{2}{T}\int_{K=K_0}^{\infty}\frac{1}{K^2}e^{rT}C(K)dk
$$
ここでFとK0がだいたい同じ程度の値であることを使って
$$
\log(1+x) \approx x-\frac{x^2}{2} \qquad (x << 1)
$$
の近似を使います。
$$
\log\frac{F}{K_0} \approx
(\frac{F}{K_0}-1) -\frac{1}{2}(\frac{F}{K_0}-1)^2
$$
より
$$
\hat{E}(V) =-\frac{1}{T}(\frac{F}{K_0}-1)^2\\
+\frac{2}{T}\int_{K=0}^{K_0}\frac{1}{K^2}e^{rT}P(K)dk \\
+\frac{2}{T}\int_{K=K_0}^{\infty}\frac{1}{K^2}e^{rT}C(K)dk
$$
積分を足し算に置き換えて、
$$
\sigma^2 \approx
\frac{2}{T}\Sigma_i\frac{\Delta K_i}{K^2}e^{rT}Q(K_i)-\frac{1}{T}[\frac{F}{K_0}-1]
$$
ということで、最終的にVIXの式がでてきました。以上です!
参考文献
1.CBOEのサイトには、計算方法が細かく記されています。
2.Wikipediaは鉄板ですね~。
3.こちらの人のノートは大変役に立ちました。
http://www-2.rotman.utoronto.ca/~hull/technicalnotes/TechnicalNote22.pdf
この記事が気に入ったらサポートをしてみませんか?
