
【行間を読む】大野木哲也・田中耕一郎「電磁気学II 物質中の電磁気学」p. 78 (E・Bの全微分形)
キーワード
電磁場の作用積分
ペンローズのグラフ記法
該当箇所
$$
L_3=-\frac{\theta}{8\pi^2}\sqrt\frac{\epsilon}{\mu}\left(\nabla\phi+\frac{∂\bm{A}}{∂t}\right)\cdot(\nabla\times\bm{A})
$$
と書ける。簡単な計算により
$$
L_3=-\frac{\theta}{8\pi^2}\sqrt\frac{\epsilon}{\mu}\left[\nabla\cdot\left(\phi(\nabla\times\bm{A})+\frac{1}{2}\bm{A}\times\frac{∂\bm{A}}{∂t}\right)+\frac{1}{2}\frac{∂}{∂t}(\bm{A}\cdot(\nabla\times\bm{A}))\right]
$$
と全微分で書かれるため(後略)
解説
計算の記法を簡略かつ直観的にするため、ペンローズのグラフ記法を用いる。以下の記事を参考のこと。
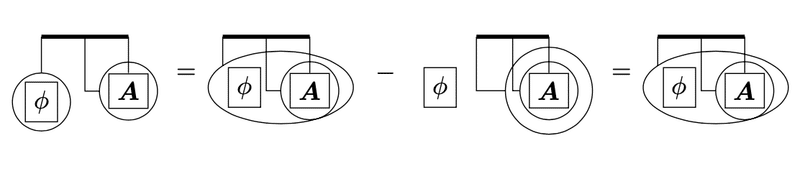
まず$${\nabla\phi\cdot(\nabla\times\bm{A})}$$を計算すると、
$$
\nabla\phi\cdot(\nabla\times\bm{A})=\nabla\cdot(\phi\nabla\times\bm{A})-\phi\nabla\cdot(\nabla\times\bm{A})=\nabla\cdot(\phi\nabla\times\bm{A})
$$
を得る。次いで時間微分を含む項は適宜ライプニッツルールを使うことで
$$
\frac{∂\bm{A}}{∂t}\cdot(\nabla\times\bm{A})=\frac{∂}{∂t}(\bm{A}\cdot(\nabla\times\bm{A}))-\bm{A}\cdot\left(\nabla\times\frac{∂\bm{A}}{∂t}\right)
$$
となる。右辺第二項を全微分形にするために、反交換関係を使ってrotの微分を移動し外積のdivを作る。ただし外積のdivにするためにはライプニッツルールを使わなければならない。すなわち

$$
\bm{A}\cdot(\nabla\times∂_t\bm{A})=-\nabla\cdot(\bm{A}\times∂_t\bm{A})+∂_t\bm{A}\cdot(\nabla\times\bm{A})
$$
の変形を要する。これを念頭に
$$
∂_t\bm{A}\cdot(\nabla\times\bm{A})=∂_t(\bm{A}\cdot(\nabla\times\bm{A}))+\nabla\cdot(\bm{A}\times∂_t\bm{A})-∂_t\bm{A}\cdot(\nabla\times\bm{A})
$$
とすれば、
$$
∂_t\bm{A}\cdot(\nabla\times\bm{A})=\frac{1}{2}\left[∂_t(\bm{A}\cdot(\nabla\times\bm{A}))+\nabla\cdot(\bm{A}\times∂_t\bm{A})\right]
$$
を得る。
この記事が気に入ったらサポートをしてみませんか?
