
【Read between lines】Srednicki "Quantum Field Theory" §18 (Superficial degree of divergence and non-renormalizability)
Key words
Non-renormalizability
Divergence
Loop diagrams
Degree of divergence
Relevant section
$$
D=[g_E]-\sum_{n=3}^\infty V_n[g_n].\qquad(18.6)
$$
This is the formula we need.
From eq. (18.6), it is immediately clear that if any $${[g_n]<0}$$, we expect uncontrollable divergences, since $${D}$$ increases with every added vertex of this type. Therefore, a theory with any $${[g_n]<0}$$ is nonrenormalizable.
Question
Why is it impossible to absorb divergence by added vertices into higher order contributions of a finite number of coefficients?
Solution
Example: φ^5 in 4-dim.
We should look at an example in 4-dim. at first. $${\varphi^5}$$ gives $${[g_5]=-1<0}$$. We introduce no interaction but $${\varphi^5}$$.
We can draw the following ladder diagram:
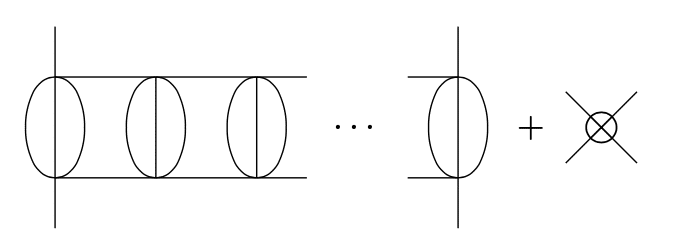
From now on, we set the ladder long enough (i.e. $${V_5\gg1}$$) to satisfy $${D=[g_E]+V_5>0}$$. When $${E=4}$$, its counter term has four legs, so we need $${(Z_4-1)g_4\varphi^4}$$ term in Lagrangian. Cutting a line of a step of the ladder, we get $${E=6}$$ diagram.
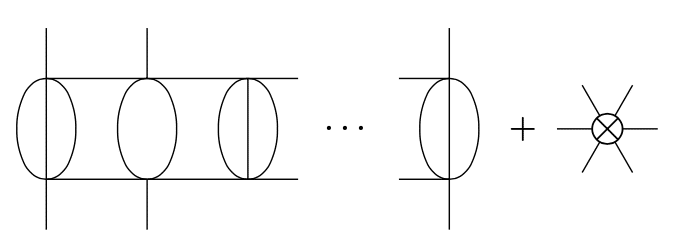
A six-leg counter term $${(Z_6-1)g_6\varphi^6}$$ is necessary. Cutting the another step,

so we have to introduce an eight-leg counter term. Cutting on and on, we get divergent ladder diagram with $${E}$$ legs ($${E}$$ is an arbitrary even number larger than 2). This means $${\varphi^5}$$ theory in 4-dim. space time is unrenormalizable.
Generalization
For any $${[g_n]<0}$$, we can draw a ladder diagram with as many steps as $${D=[g_E]-V_n[g_n]>1}$$ for given $${[g_E]}$$. When renormalizing this diagram we have to manipulate $${Z_E}$$. $${E}$$ is arbitrary, so that it is necessary to adjust infinite number of coefficients, i.e., the theory is unrenormalizable.
この記事が気に入ったらサポートをしてみませんか?
