
BigQuery ML の時系列モデル ARIMA_PLUS が季節成分・トレンド成分分解に利用するアルゴリズムの検証
これは、BigQuery Advent Calendar 2023 の 3 日目の記事です。
※先に公開していた下記の記事(メモ)をまとめ直した完全版となります。
この記事は?
BigQuery ML (以下 BQML) の時系列モデル ARIMA_PLUS が内部で動かしているアルゴリズムのうち、季節成分・トレンド成分分解の詳細を明らかにすべく、R で実装したモデルとの比較実験を行った。
サマリー
公式ドキュメントの記述からは、BQML の ARIMA_PLUS において季節成分・トレンド成分分解は以下の操作を実行しているものと読み取ることができる(下図も参照):
入力時系列データから STL という手法によって季節成分を推定する
「1.」で得られた季節成分を差し引いた残差成分から ARIMA モデルを作成し、その予測値をトレンド成分と見做す

この解釈が合っているかを検証するために R で上記と同様の実装を行い、BQML によるモデリング結果との比較を行った。
その結果、季節成分については BQML ARIMA_PLUS による推定値と R によるモデル推定値が一致し、トレンド成分も一致はしなかったものの大局的には近い変動をもつ推定値が得られた。
したがって、ARIMA_PLUS の内部アルゴリズムのうち季節成分・トレンド成分分解は上記に述べたような処理が行われていることが概ね確認できた。
背景
ARIMA_PLUS とは?
ARIMA_PLUS は BQML が提供する時系列モデリングオプションであり、未来の値の予測のほか、ML.EXPLAIN_FORECAST() 関数を用いることでトレンド成分・季節成分・祝日効果・外れ値(spikes_and_dips)・ステップ状変化点(step_changes)といった成分分解表示も行うことができる。
内部アルゴリズムについて公式ドキュメントの記述からわかること
ARIMA_PLUS はその名前が示すように、古典的な時系列アルゴリズムとして有名な ARIMA モデルをベースにしている。
しかし、その詳細な内部アルゴリズムについて解説した資料は本記事公開の2023年12月時点で存在していない。
唯一、上記公式ドキュメントの "Time series modeling pipeline" という節に図と共に大まかな説明がなされている。
これに基づくと、大まかには以下のような処理の流れを実行していると解釈できる:
0.前処理(重複データの処理、データ間隔の調整、欠損値補完)
↓
1.祝日効果の除去
↓
2.外れ値除去
↓
3.季節成分除去 (STL使用)
↓
4.ステップ状変化点除去
↓
5.トレンド成分の推定 (ARIMA モデル使用)
これらのうち、「1.祝日効果の除去」「2.外れ値除去」「4.ステップ変化除去」については、具体的にどのようなアルゴリズムが利用されているか言及がなく、現状完全にブラックボックスである。
一方、「3.季節成分除去」で使われる STL と「5.トレンド成分の推定」で使われる ARIMA モデルは時系列解析ではよく知られた手法であり、アルゴリズムの検証が可能である。
以降はこの季節成分・トレンド成分の分解に焦点を当てる。
季節成分・トレンド成分の分解方法
3.の季節成分除去で使われている STL という手法は、Seasonal and Trend decomposition using Loess といって、時系列を季節成分+トレンド成分+残差成分に分解する際に一般的に使われる手法であり、 R の 標準パッケージである stats や Python の statsmodels にもそれぞれ実装されている。
ただしドキュメントの図と説明によると、ここで得られた成分のうち実際に推定結果として使われるのは季節成分だけで、残りの入力データから deseasonalized された成分は後段のモデリング処理の入力として回される。
そして、4.の変化点除去を経たのち、ARIMA モデルにて改めてトレンド成分の推定が行われるものと読み取ることができる。
(なぜ STL で得たトレンド成分をそのまま使わないのか?という疑問が当然湧くが、おそらくは予測精度を上げるためであろう。)
ARIMA モデルももちろん、 STL 同様 R (stats) 、Python (statsmodels) 両方で実行が可能である。
背景まとめ
まとめると、ARIMA_PLUS におけるトレンド成分・季節成分の推定は STL と ARIMA モデルを組み合わせたものとして解釈でき、さらにこの部分に限ると R や Python など他の環境であっても BQML による出力結果を再現できると考えられる。
ただし、本当にこの解釈で正しいかについては検証の余地があるため、以降これを確かめるべく実験を行う。
実験内容
目的
ARIMA_PLUS による季節成分・トレンド成分分解が以下のようなアルゴリズムで行われているという仮説を立て、これを検証する。
入力時系列データ から STL によって季節成分を推定する
入力データから「1.」で得られた季節成分を差し引いた残差成分に対して ARIMA モデルを作成し、その予測値をトレンド成分と見做す
実験方法
祝日効果・外れ値・変化点の存在しない時系列データに対して R を用いて上記に相当するモデリングを行い、モデル推定結果が BQML による推定結果と一致するかを調べた。
実験対象データ
以下のような(1,1,2)次の ARIMA 過程により生成された系列データ(トレンド成分に相当)にsin 関数による 7周期成分とランダムノイズを付加した人工データを用いた。
library(ggplot2)
library(gridExtra)
set.seed(13)
tr <- 1.2 * arima.sim(model=list(order=c(1,1,2), ar=c(0.8), ma=c(0.2, -0.8)), n=99)
s <- 10 * sin(seq(0, 99, length.out=100) * 2 * pi / 7)
y <- tr + s + rnorm(100)
time.points <- seq.Date(as.Date("2014-01-01"), by=1, length.out=100)
data <- data.frame(day=time.points, y=y, trend=tr, seasonal=s)
p1 <- ggplot(data=data) +
geom_line(aes(x=day, y=y))+
labs(x="day", y="y")
p2 <- ggplot(data=data) +
geom_line(aes(x=day, y=trend))+
labs(x="day", y="trend")
p3 <- ggplot(data=data) +
geom_line(aes(x=day, y=seasonal))+
labs(x="day", y="seasonal")
grid.arrange(p1, p2, p3)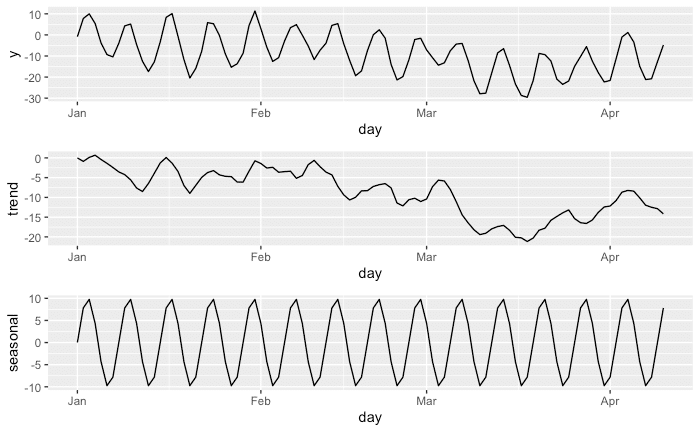
モデル作成
BQML ARIMA_PLUS によるモデル
まずは、上記のデータをもとに BQML の ARIMA_PLUS モデルを作成した。
詳細なクエリ等はこちらのメモを参照のこと。
作成したモデルをもとに ML.EXPLAIN_FORECAST() 関数で成分分解をした結果が以下である(作図は R で行った)。

上から全成分、季節成分、トレンド成分。
なお、このとき周期成分 (seasonal_period_*) は weekly のみ値が入っており、入力データの生成過程の通り7周期として推定できていたことがわかる。
一方、この時の ARIMA 係数を ML.ARIMA_COEFFICIENTS() 関数で確認したところ、トレンド成分は 4 次の MA 過程((0,0,4)次の ARIMA 過程)として推定が行われていた。
その他、祝日効果(holiday_effect)、外れ値(spike_and_dips)、変化点(step_changes) については値が含まれておらず、これらの成分は存在しないとしてモデル推定がなされていた。
したがって、「祝日効果・外れ値・変化点は含まない」とする前提を満たしていることが確認できた。
R によるモデル作成
詳細なモデル作成方法はこちらのメモに譲るが、実験対象データをもとに、STL で季節成分を推定し、さらに残りの成分から ARIMA モデルによりトレンド成分を推定した。
その結果、以下のグラフのようになった。

上から全成分、季節成分、トレンド成分。
なお、トレンド成分を ARIMA モデルで推定する際、次数は BQML による結果に合わせて (0,0,4) に指定した。
BQML の結果と R の結果の比較
以上で BQML と R それぞれのモデリング結果が出揃ったので、比較を行う。例によって比較方法の詳細なコードはこちらのメモに譲る。
季節成分
以下は、季節成分のBQML ARIMA_PLUS による推定値(青)と R の STL による推定値(黒実線)を並べたものである。

ここからわかるように、両モデルの季節成分推定値がほぼ一致した。
一致具合を定量的に評価するために平均絶対誤差を計算したところ、 $${7.295137\times 10^{-15} }$$ と極めて小さかった。
トレンド成分
次に、トレンド成分のBQML ARIMA_PLUS による推定値(青)と R の STL による推定値(黒実線)を並べたものを見てみる。

こちらについては、細かくみると両モデルで推定値が一致しないものの、大局的な変動傾向は真のトレンド(データ生成時に与えたもの、上図点線)に沿っており概ね似ていることが(定性的にではあるが)見てとれる。
考察
以上、BQML の ARIMA_PLUS による季節成分・トレンド成分検出アルゴリズムを特定できないかと R で STL と ARIMA モデルを組み合わせたモデリングを行なってみた。
その結果、季節成分は BQML による結果と一致した。
一方で、トレンド成分は一致こそしなかったものの、大局的な変動傾向は両モデルで近く、共にデータ生成時に用意した真のトレンドに沿った動きをしていた。
したがって当初の推測通り、ARIMA_PLUS の内部アルゴリズムのうち季節成分・トレンド成分の推定には、それぞれ STL で推定した季節成分と deseasonalized された時系列に対する ARIMA モデルを利用しているという理解で概ね正しそうだと確認できた。
なお、トレンド成分が厳密に一致しない原因として考えられる要因としては、ARIMA のパラメータ推定アルゴリズムの差異が考えられる。
ARIMA 過程において、係数パラメータの推定には大抵の場合カルマンフィルタ(AR過程なら最小二乗法)が用いられるため実装による差は小さい。しかし、誤差項分散パラメータの推定には準ニュートン法などの最適化手法を用いるため、用いる手法や初期値の置き方次第では異なる結果が得られても不思議でない。
この記事が気に入ったらサポートをしてみませんか?
