ふりこの動き(5年)を考える！

「ふりこ」の学習の新しい視点を考えた。

理科の見方・考え方の視点で切り取って考えてみると新しい教材の価値に気づく。

条件制御を学ばせるという視点で学習を組み立てることもできるが、今回提案したいのは、条件制御した条件の一つ一つで価値を持った学習ができるという点である。

さらに、学習する順番にも論理がある。

まずは、子供に振り子を提示する。振り子とは何であるかを定義する必要がある。
「上端を固定した糸の先におもりをつけ糸がたゆまないように横に引いて同じ位置までついたら往復をするもの」
ウィキペディアでは、
『振り子（ふりこ、英: pendulum）とは、空間固定点（支点）から吊るされ、重力の作用により、揺れを繰り返す物体である。 支点での摩擦や空気抵抗の無い理想の環境では永久に揺れ続ける。 時計や地震計などに用いられる。』
となる。

また、言葉の定義も大切である。
科学的思考は、指し示す範囲が限定された言葉によってなされる方である。
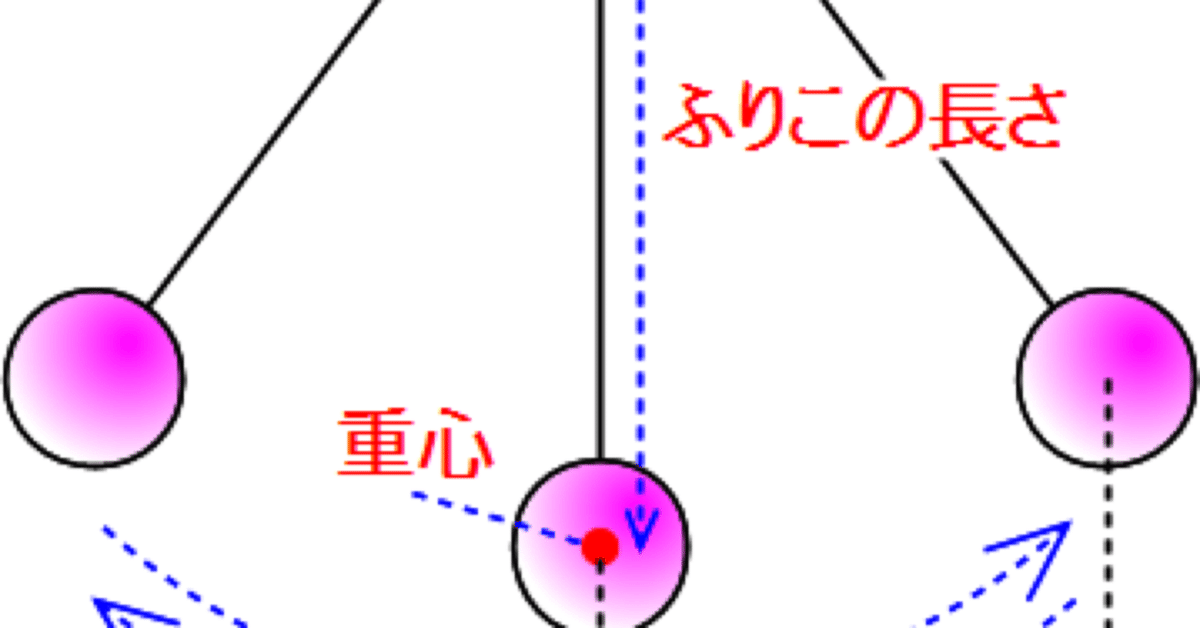
「ふれはば」
「おもり」
「ふりこの長さ」
「一往復」
とは何を指し示すかを定義する。

その上で、自由な試行活動を行い、現象から「問い」を生み出させる。

つぎに、測定の技能を高める。
測定させながら正確に１往復を測ることの難しさを感じさせながら、誤差が出ることに気づかせる。
だから、１０往復する時間を測って、１０で割ることで１往復の時間を求めることを学習する。
しかし、１０往復の最初の１往復の時間と最後の１往復の時間は、ちがっていると考える子供もいる。
だから、条件制御の最初は、「ふれはば」を扱う。
「ふれはば」がちがっても１往復する時間が変わらないことが分かる。だから、１０往復させたうちのどの１往復をとってみても往復する時間は変わらない。つまり、１０往復した時間を測ってそれを１０で割ると１往復の時間を求めることができることの証明になっている。
さらに、「ふれはば」での学びは、それだけではない。ふりこの法則がなりたつのは、限定された範囲だからである。
「ふれはば」が大きすぎると１往復する時間が変わってしまう。
９０度の位置からふりこを振る。すると、反対側の８０度ぐらいの位置までしかふりこが到達しない。位置エネルギーが変わってしまう。同じ場所まで行ってないので、１往復の時間が変わっているのが分かる。次は、８０度・・・と１０度づつ下げて実験を繰り返すと４０度の位置で左右が対象になる。つまり、「ふれはば」が最大４０度以下の範囲で成り立つきまりを探すことが実験によって確かめられる。

ここで押さえるのは、「ふれはば」では、１往復の時間は変わらないことと「ふりこの長さ」５０cm、「おもり１個」のときに１往復する時間が約1.4秒となることを基準とすることである。

さらに、次の条件は、「ふりこの長さ」である。
ここでは、量的・関係的な理科の見方をする。
「ふりこの長さ」が５０cmのときに１往復する時間が約1.4秒になることから予想を立てる。
「ふりこの長さ」１００cmのときは、１往復する時間が何秒になるかを考える。変わらないという意見と２倍にになると意見。２倍まではならないが変わるという意見。基準があるから思考できる。
ここで、ふりこの１往復する時間は、0.1秒の単位での変化が問題になるということに気づく。だから、0.01秒の単位の違いは、誤差と認定できるわけである。
だから、0.01秒の位を四捨五入してデータを記入することができる。

最後の条件が、「おもりの重さ」である。
おもりの重さを変えると1往復の時間が変わると思っている子どもは、多い。
ここでは、学びに向かう人間性のうち「結果を謙虚に受け止める」ということを学ばせるために扱う。ここで大切になるのは、「自らの活動を客観的に振り返り、条件制御等を意識して再検証すること。」である。だから、再検証の時間が必要になる。

これらの一つ一つの学習活動に意味があることとして捉え、授業を展開していくことが必要になる。