書記が数学やるだけ#80 等角写像，1次写像

複素関数のラストとして，等角写像を扱うことにする。

問題

等角写像の中でも代表的な，円円対応についての問題である。

説明

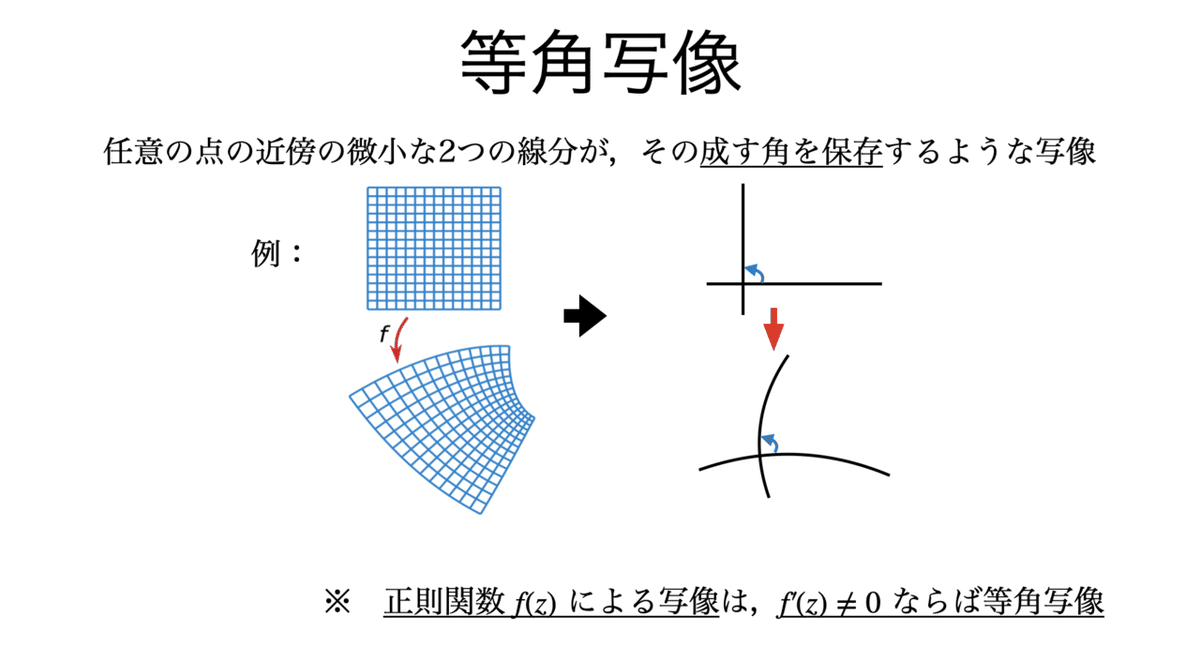
複素関数について，1次写像を分解すると，3つのタイプの合成写像の組み合わせで表現できることがいえる。

ここで，無限遠点を追加することで，複素平面はリーマン球面に拡張される。

最後に，複素関数からいえる重要な定理をいくつか列挙しておく。

ここまできて，なんと複素関数が代数学と結びつく。

解法

まずは題意を読み取る。

あとはひたすら計算するだけである。

これで複素関数の解説を一旦シメとしたい。複素関数に拡張することで，見える世界が広がるほかに，数全体に言える基本原理を見直すことにもつながる。応用上重要なのは留数定理であり，計算練習を重ねておきたい。それだけでなく，代数学の核心に迫るための重要な材料である，ということも頭に入れておきたい。

本記事のもくじはこちら：