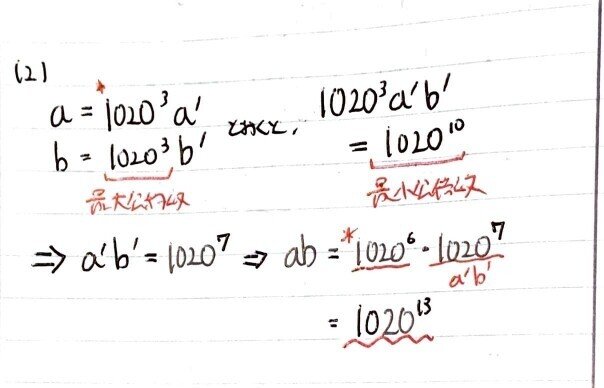書記が数学やるだけ#73 合同式の基本操作,中国剰余定理
休憩(?)として,大学入試からその後まで幅広く用いられる合同式について,いくつか話題を提供する。
今回は基本操作と中国剰余定理について,次回はフェルマーの小定理について扱うことにする。
過去に平方剰余について扱った記事があるのでそちらも参照。
問題
前座として,見るからに合同式を使う問題。
中国剰余定理について,「孫子算経」が元とされている。
説明
整数の割り算について余りを考えるのが合同式の始まり。
重要なのは和と積についての式。
そこから累乗においても合同であることが言える(証明について,2018年京都府大/生命環境にて出題)。これがとても便利なもので,例え何乗して膨大な数になっても余りが簡単にわかるようになる。
中国剰余定理について,「孫子算経」にこのような問題がある。
引用元:
https://ctext.org/sunzi-suan-jing/zh
今有物,不知其數。三、三數之,賸二;五、五數之,賸三;七、七數之,賸二。問物幾何?
答曰:二十三。
術曰:「三、三數之,賸二」,置一百四十;「五、五數之,賸三」,置六十三;「七、七數之,賸二」,置三十。并之,得二百三十三。以二百一十減之,即得。凡三、三數之,賸一,則置七十;五,五數之,賸一,則置二十一;七、七數之,賸一,則置十五。一百六以上,以一百五減之,即得。
この問題は「孫子算経」とともに日本にも伝わり,後に和算の隆盛した江戸時代には「百五減算」として知られた。のちに,ガウスは「整数論」(1801年)で,以下に示す中国剰余定理の証明を行なった。
解法
累乗における合同を利用することで,剰余を絞り込むことができる。
最小公倍数と最大公約数からabの値はわかる。
合同式の基本操作を駆使して,それぞれの剰余を求めていく。
最後にaとbそれぞれの値を出す。和と差の剰余から候補を割り出す。
中国剰余定理の問題。
孫子算経に書かれていた解法はこちらである。
これを,連立合同式を立てて地道に解くとこうなる。
中国剰余定理は,現代では暗号理論において重要な役割を果たしている。
参考:
本記事のもくじはこちら: