【集合】6 同値関係と商集合

こんにちは、これが328本目の記事となったすうじょうです。今日は、大学数学の解説記事です。今回の内容は、集合論より同値関係と商集合を解説します。(演習問題の解答を修正しました)

この記事は、以下の記事の続きです。

ただ、前提知識としては上の記事よりも次の記事の内容の理解が必要です。

同値関係

同値関係の定義

集合$${A}$$上の二項関係$${R}$$が反射律、対称律、推移律を満たすとき、 $${R}$$を同値関係という。

一般に同値関係の話をするとき、$${R}$$の代わりに記号$${\sim}$$を用いることとする。

同値関係の例としては、兄弟姉妹関係がある。ただし、自分自身は自分の兄弟姉妹であるとする。その具体例を以下に示す。

$${A＝}$${大和,凛,悠斗,空,優斗,芽衣,日葵}上の二項関係$${R_S = }$${(大和,大和),(凛,凛),(悠斗,悠斗),(空,空),(優斗,優斗),(芽衣,芽衣),(日葵,日葵),(大和,凛),(大和,優斗),(大和,悠斗),(大和,空),(凛,大和),(凛,悠斗),(凛,空),(悠斗,大和),(悠斗,凛),(悠斗,空),(空,大和),(空,凛),(空,悠斗),(優斗,芽衣),(優斗,日葵),(芽衣,優斗),(芽衣,日葵),(日葵,優斗),(日葵,芽衣)}とする。

$${(x,y)\in R_S}$$のとき、$${x}$$は$${y}$$の兄弟姉妹という二項関係である。

この二項関係$${R_S}$$は同値関係の条件である反射律、対称律、推移律をそれぞれ満たしている。

他の同値関係の例としては、 $${\N}$$上の二項関係(相等関係)$${=}$$がある。以下のようにして、条件を満たしていることを確認できる。
$${x=x}$$は常に成り立つので、反射律を満たす。
$${x=y}$$のとき$${y=x}$$なので、対称律を満たす。
$${x=y}$$かつ$${y=z}$$のとき$${x=z}$$なので、推移律を満たす。

同値関係では、「同じものどうし」が順序対として要素になっている。$${A}$$上の兄弟姉妹関係$${R_S}$$の例では、$${A}$$上で「同じ家族の人どうし」が同値関係となっている。$${\N}$$上の相等関係$${=}$$の例では、「同じ数どうし」が同値関係となっている。

同値類と商集合

$${A}$$上の同値関係$${\sim}$$があるとき、$${A}$$のある要素$${x}$$に対して$${x}$$と同値関係$${\sim}$$にあるすべての要素からなる集合を同値類といい、$${[x]_\sim}$$または$${C(x)}$$と表す。この定義は以下のように書くことができる。

$${[x]_\sim = \{y \in A| x \sim y\}}$$

$${x}$$のことを代表元という。代表元とする要素はその同値類に含まれる要素であればどれでもよい。

同値類は、同値関係にある要素を集めて、もとの集合を分割してできた集合となっている。

$${A}$$上の同値関係$${\sim}$$があるとき、$${A}$$を同値関係$${\sim}$$により分割してできた集合である同値類の集合を商集合という。この定義は以下のように書くことができる。

$${A/\sim \space = \{[x]_\sim| x \in A\}}$$

商集合は、同値関係による集合の分割となっている。

※集合の分割とは
ここまで集合の分割という言葉を使ってきたが、これは厳密に定義できる。
集合$${A}$$の部分集合からなる集合$${\{A_1,A_2,…,A_n\}}$$が次の条件を満たすとき、$${\{A_1,A_2,…,A_n\}}$$を$${A}$$の分割という。
$${\textrm{(i)} A_i \neq \empty \space (i =1,2,…,n)}$$
$${\textrm{(ii)} A=\displaystyle\bigcup_{i=1}^n A_i}$$
$${\textrm{(iii)} S_i \neq S_j \to S_i \cap S_j = \empty}$$
つまり、集合の要素を重複なく分けあった集合の集合のことを集合の分割という。
上で書いた一般に商集合が集合の分割となっていることはこの定義にしたがって証明でき、問題17の後ろの※でその証明をした。

$${A＝}$${大和,凛,悠斗,空,優斗,芽衣,日葵}上の二項関係である兄弟姉妹関係$${R_S}$$について、同値類と商集合を考える。

同値類は以下の2つである。
$${[\text{大和}]_{R_S}=}$${大和,凛,悠斗,空}
$${[\text{優斗}]_{R_S}=}$${優斗,芽衣,日葵}
よって、$${A}$$の$${R_S}$$による商集合は
$${A/R_S=\{[\text{大和}]_{R_S},[\text{優斗}]_{R_S}\}=}$${{大和,凛,悠斗,空},{優斗,芽衣,日葵}}

図13:AのRsによる商集合のイメージ

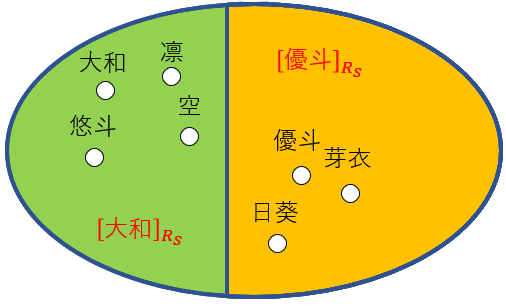
同値類は、「同じものどうし」という関係を表す同値関係で、「同じものどうし」とわかったものをひとまとまりにしたもの(グループ分けしたもの)となっている。$${A}$$上の兄弟姉妹関係$${R_S}$$の例では、$${A}$$上で「同じ家族の人」がそれぞれ同値類となっている。

同値関係の比較

$${A}$$上の2つの同値関係$${\sim,\approx}$$があるとき、それぞれの商集合$${A/\sim,A/\approx}$$がどの程度$${A}$$を分割しているかを比較する用語とその定義を以下に示す。

$${\sim}$$は$${\approx}$$より細かい（$${\approx}$$は$${\sim}$$より粗い）
$${\xLeftrightarrow{def} \forall x, \forall y \in A, x \sim y \to x \approx y}$$

この定義は商集合の要素である同値類を用いて以下のように表現することもできる。
$${\sim}$$は$${\approx}$$より細かい（$${\approx}$$は$${\sim}$$より粗い）
$${\xLeftrightarrow{def} \forall X \in A/\sim, \exists Y \in A/\approx, X \subseteq Y}$$
個人的にはこの定義のほうが言葉の印象と合う気がします。

$${\sim}$$が$${\approx}$$より細かいとき、商集合について以下の関係が成り立つ。ただし、集合$${A}$$の要素数を$${|A|}$$と表すこととする。
$${|A/\sim| \geq |A/\approx|}$$

演習問題6

問題15 $${\Z}$$上の二項関係$${\equiv _n}$$を次のように定義するとき、次の各問に答えよ。
$${a \equiv _n b (nは2以上の整数)\xLeftrightarrow{def} \exists k \in \Z \space s.t. \space a-b=kn}$$
この関係が成り立つとき、$${a}$$と$${b}$$は$${n}$$を法として合同であるという。
(1)二項関係$${\equiv _n}$$が同値関係であることを証明せよ。
(2)$${3}$$を法とする合同関係$${\equiv_3}$$について、商集合$${\Z/\equiv_3}$$を求めよ。
(3)$${6}$$を法とする合同関係$${\equiv_6}$$について、商集合$${\Z/\equiv_6}$$を求めよ。
(4)$${\Z}$$上の同値関係$${\equiv_3}$$と$${\equiv_6}$$について、その細かさを比較せよ。

[方針]
問題の同値関係は合同関係といい、$${a \equiv b (\textrm{mod} \space n)}$$と書くこともある。この意味は、$${a}$$を$${n}$$で割ったときの余りと$${b}$$を$${n}$$で割ったときの余りが等しいというものである。

[証明]
(1)
$${\Z}$$上の二項関係$${\equiv _n}$$が反射律, 対称律, 推移律を満たすことを示せばよい．
$${\forall x \in \Z, x-x=0=0\times n}$$
よって, 反射律を満たす．
$${\forall x, \forall y \in \Z, x \equiv _n y}$$のとき,
$${\exists k \in \Z \space s.t. \space x-y=kn}$$
$${\Rightarrow \exists (-k) \in \Z \space s.t. \space y-x=(-k)n}$$
$${\Rightarrow \exists l \in \Z \space s.t. \space y-x=ln}$$
よって, 対称律を満たす．
$${\forall x, \forall y, \forall z \in \Z, x \equiv_n y \land y \equiv_n z}$$のとき,
$${(\exists k_1 \in \Z \space s.t. \space x-y=k_1n) \land (\exists k_2 \in \Z \space s.t. \space y-z=k_2n)}$$
$${\Rightarrow \exists k_1, \exists k_2 \in \Z \space s.t. \space x-z=(k_1-k_2)n}$$
$${\Rightarrow \exists l \in \Z \space s.t. \space x-z=ln}$$
よって, 推移律を満たす．$${\Box}$$
[解答]
(2)
$${\equiv_3}$$の同値類を考えると,
$${[1]_{\equiv_3}=\{…,-5,-2,1,4,7,…\}=\{3n+1|n \in \Z\}}$$
$${[2]_{\equiv_3}=\{…,-4,-1,2,5,8,…\}=\{3n+2|n \in \Z\}}$$
$${[3]_{\equiv_3}=\{…,-6,-3,0,3,6,9,…\}=\{3n|n \in \Z\}}$$
よって, 商集合は
$${\Z/\equiv_3=\{[1]_{\equiv_3},[2]_{\equiv_3},[3]_{\equiv_3}\}=\{\{3n+1|n \in \Z\},\{3n+2|n \in \Z\},\{3n|n \in \Z\}\}}$$
(3)
$${\equiv_3}$$の同値類を考えると,
$${[1]_{\equiv_6}=\{…,-11,-5,1,7,13,…\}=\{6n+1|n \in \Z\}}$$
$${[2]_{\equiv_6}=\{…,-10,-4,2,8,14,…\}=\{6n+2|n \in \Z\}}$$
$${[3]_{\equiv_6}=\{…,-9,-3,3,9,15,…\}=\{6n+3|n \in \Z\}}$$
$${[4]_{\equiv_6}=\{…,-8,-2,4,10,16,…\}=\{6n+4|n \in \Z\}}$$
$${[5]_{\equiv_6}=\{…,-7,-1,5,11,17,…\}=\{6n+5|n \in \Z\}}$$
$${[6]_{\equiv_6}=\{…,-12,-6,0,6,12,18,…\}=\{6n|n \in \Z\}}$$
よって, 商集合は
$${\Z/\equiv_6=\{[1]_{\equiv_6},[2]_{\equiv_6},[3]_{\equiv_6},[4]_{\equiv_6},[5]_{\equiv_6},[6]_{\equiv_6}\}=\{\{6n+1|n \in \Z\},\{6n+2|n \in \Z\},\{6n+3|n \in \Z\},\{6n+4|n \in \Z\},\{6n+5|n \in \Z\},\{6n|n \in \Z\}\}}$$
(4)
$${\equiv_6}$$は$${\equiv_3}$$より細かい

問題16 $${S=\{1,2,3,4\}}$$とする。$${R}$$を$${S}$$上の同値関係とするとき、 $${S/R}$$は全部で何個あるか。

[方針]
商集合は、集合の分割で、集合の要素を重複なく分けあった集合(同値類)の集合となっている。よって、すべての分け方を列挙すればよい。
同値関係は、同値類のもととなる関係なので、この問題の答えは、$${S}$$上の同値関係が何個あるかという問題と等価である。

[解答]
$${\{\{1\},\{2\},\{3\},\{4\}\}}$$
$${\{\{1,2\},\{3\},\{4\}\}}$$
$${\{\{1,2\},\{3,4\}\}}$$
$${\{\{1,3\},\{2\},\{4\}\}}$$
$${\{\{1,3\},\{2,4\}\}}$$
$${\{\{1,4\},\{2\},\{3\}\}}$$
$${\{\{1,4\},\{2,3\}\}}$$
$${\{\{2,3\},\{1\},\{4\}\}}$$
$${\{\{2,4\},\{1\},\{3\}\}}$$
$${\{\{3,4\},\{1\},\{2\}\}}$$
$${\{\{1,2,3\},\{4\}\}}$$
$${\{\{1,2,4\},\{3\}\}}$$
$${\{\{1,3,4\},\{2\}\}}$$
$${\{\{2,3,4\},\{1\}\}}$$
$${\{\{1,2,3,4\}\}}$$
よって, 15個

問題17 $${R}$$を集合$${X}$$上の同値関係とするとき、次のことが成り立つことを証明せよ。
(1)$${\forall x \in X, x \in [x]_R}$$
(2)$${x R y \Lrarr [x]_R=[y]_R}$$
(3)$${[x]_R \cap [y]_R \neq \empty \Rightarrow [x]_R = [y]_R}$$

[証明]
(1)
$${R}$$は反射律を満たすので, $${x R x}$$
$${[x]_R}$$の定義より, $${x \in [x]_R}$$     $${\Box}$$
(2)
まず, $${x R y \Rightarrow [x]_R=[y]_R}$$について示す．
$${x R y}$$のとき, $${([x]_R \subseteq [y]_R) \land ([y]_R \subseteq [x]_R)}$$を示せばよい．
(1)より, $${\forall z \in X, z \in [x]_R}$$
同値類の定義より, $${x R z-①}$$
前提より, $${x R y}$$
同値関係の対称性より, $${y R x-②}$$
$${①, ②}$$, 同値関係の推移性より, $${y R z}$$
よって, $${z \in [y]_R}$$
部分集合の定義より, $${[x]_R \subseteq [y]_R}$$
同様にして, $${[y]_R \subseteq [x]_R}$$
以上より, $${[x]_R=[y]_R}$$
次に, $${[x]_R=[y]_R \Rightarrow x R y}$$について示す．
(1)より, $${\forall x \in X, x \in [x]_R}$$
ここで, $${[x]_R=[y]_R}$$より, $${x \in [y]_R}$$
同値類の定義より, $${y R x}$$
同値関係の対称性より, $${x R y \qquad \Box}$$
(3)
$${[x]_R \cap [y]_R \neq \empty}$$のとき,
$${\exists a \in [x]_R \cap [y]_R}$$
$${\Rightarrow a \in [x]_R \land a \in [y]_R}$$
$${\Rightarrow x R a \land y R a (\because 同値類の定義)}$$
$${\Rightarrow x R a \land a R y(\because 同値関係の対称性)}$$
$${\Rightarrow x R y(\because 同値関係の推移性)}$$
$${\Rightarrow [x]_R=[y]_R(\because (2))\qquad \qquad \qquad \qquad \Box}$$

※問題17で証明したことを用いると、商集合が集合の分割となっていることを証明できる。ここでは、問題17の命題を前提とした証明を示す。(他の命題を前提とした証明もあり、この証明は一例である)
商集合$${A/\sim}$$が集合$${A=\{a_1,a_2,…,a_n\}}$$の分割であることを示す。
(1)$${\forall a \in A, a \in [a]_\sim}$$より, $${[a_1]_\sim \cup [a_2]_\sim \cup … \cup [a_n]_\sim= \displaystyle\bigcup_{i=1}^n [a_i]_\sim=A}$$
(3)$${[x]_\sim \cap [y]_\sim \neq \empty \Rightarrow [x]_\sim = [y]_\sim}$$の対偶は,
$${[x]_\sim \neq [y]_\sim \Rightarrow [x]_\sim \cap [y]_\sim = \empty}$$
以上より, 商集合$${A/\sim}$$は集合$${A}$$の分割である。

最後に

今回は、大学数学・集合論の解説記事として、同値関係と商集合について解説しました。次回は、写像・関数の解説記事となる予定です。では。

この記事の続きは以下の記事です。