【線型代数】A:n次正方行列　A^2=A の解①

　夏休みの間『線型代数入門』(齋藤正彦著)(以下教科書)と格闘しています。まだ通読していませんが、５章の固有値から急に読む速度が落ちました。

　未習範囲ということも原因の一つだと思いますが、自明とは思えない命題の証明が所々端折られているんですよね・・・。(見落としている？)　あと単純に教科書に載ってある証明を理解するのに時間がかかります。数学書を読むことについては経験値が足りていないので、一つ一つ自分の中で納得して少しずつ読み進めるしかないですね。他にこの教科書を使っている人がいたら、分からないところについて話し合いたいなーとか思っています。

　久しぶりに長い(?)文章を書いているので、グダグダになっていますね。本題に移りましょう。(『線型代数入門』p143~144の内容です。)

　単刀直入に言うと、今回のテーマはタイトルにもあるように

「A:n次正方行列 A=A^2  を満たすAはなんだろう？」

です。線型代数を習いたての時にこの疑問が浮かんできたのですが、その時はまだ解決する道具が自分の中に揃っていませんでした。しかし、固有値周りの内容まで学習を進めて、自分のなかで解ける兆しが見えてきたので、noteにまとめてみようと思います。

※記号のお約束。

示したい命題番号：(1),(2),...

証明に使う定理につける番号：①,②,...

こういうの難しいですね。式番号ぐっちゃぐちゃになったり、勝手に記号を使ったりしてるところも出てくると思います。すみません。

1.射影子は「固有値が0または1のエルミート変換」

(本題は次の章から始まります。)

ユニタリ空間Vに対し、射影子という線型変換 P:V→Vは

と特徴付けられる線型変換です。教科書では別の定義からこれを証明した後、

「さらに、射影子とは、「固有値が全て1または0であるようなエルミート変換」であると言うこともできる。」-(1)

という一言が添えられています。最初にこれを見たときに「？？？」となったので、備忘録という意味も込めて(1)を証明します。

以下、線型変換Pの任意の基底に関する表現行列Aについての話に置き換えます。(ごちゃごちゃしてます。すみません。)　つまり、示したい命題は以下の命題です。

示します。

示すことができました。時間はかかりますが、このように自分で証明を考えるのは楽しいですね。

2.A=A^2　の解は？(本題)

さて、ここからが本題です。(1)'の証明の途中で「A=A^2⇒Aの固有値は0または1」を示すことができました。つまり、「行列の方程式」 A=A^2 の解Aが満たす必要条件を求めたことになります。では A=A^2 の解Aが満たす必要十分条件は何でしょうか？それについて調べたことを以下述べていきます。

まず以下の命題を示します。

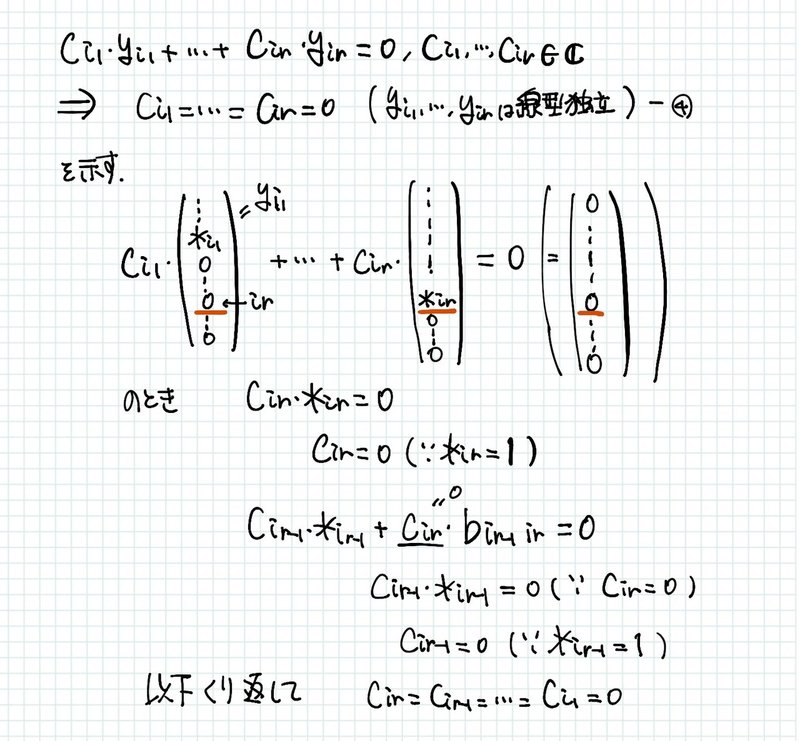
次に本題となる命題を示します。

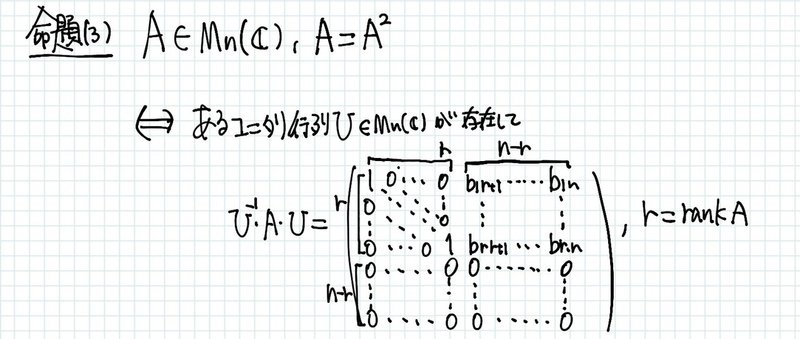
⑦も同様に示します。

これにて、A=A^2 の解Aの必要十分条件を求めることができました！

しかし、(3)⇒中の証明で出てきた

ここの部分が附に落ちてないんですよね。もっともらしく書きましたが、自分の中では証明できていません。

「ユニタリ行列Uをどう構成するか」「Uによって上三角化した後の対角成分がどう並ぶのか」がまだあまり分かっていないので、そこを調べていきたいですね。

3.今後

上で述べたことの繰り返しになりますが、

・ユニタリ行列Uを具体的に構成する。UとU^(-1)AU の対角成分がどのように並ぶのかの関係性を調べる。

を続編にしようかなと思います。

また、そのまたさらに続きとして

・その他の「行列の二次方程式」、「行列の三次方程式、n次方程式」「代数方程式との比較」などを調べる。

ことも考えています。

間違い、追加の考察などあればTwitterなどで言っていただけると嬉しいです。(アカウント：http://twitter.com/321akki_)

画像ばかりの記事になってしまいましたね。先日Latexを導入しましたが、結局Latexを使うより自分で書く方が早いので、全然使う機会がありません。noteでLatexは使えたりするのだろうか？もしそうだったら練習がてら使ってみようかな。

それではまた。