積分はなぜ微分の逆で、面積計算なのか

サムネイラストですが、積分ということで、積分記号 ∫（インテグラル）にちなみ、ヘルシングの主人公、インテグラを描いてみました。

・・・似てますかね。

前置きはこの辺にして、

以前、高校数学の山場である微分について、「何の意味があるのか？」という趣旨の記事を書きました。

今回は、もう一つの山場、微分の対になる事案、積分について書いていきたいと思います。積分といったらとりあえずこの形ですよね。

これ、積分のパートに入ったら、いきなり記号が出てくるんですよね。「積分を表現するときは ∫ という記号を使うんです。」ていうだけなら、まあそういうもんかって、受け入れられるんですが、なんで dx を後ろにつけないといけないのか。そういう説明を学校ではしてくれたでしょうか？

私の学校ではお約束の

そういうもんだから覚えろ )>( ﾟД ﾟ)

の一言で片付けられました。そういうのが嫌だってのに。。学校の数学教育・・・、困ったもんです。地頭で理解する能力が最も問われるのが数学だと思うんですが・・・、考えることを放棄させるような教え方は、数学を学ぶ本来の趣旨という観点からみても問題があると思います。

まあ、それはそれとして、本記事では積分の意味するところを掘り下げていきます。

微分が傾きを求める計算であったのに対し、積分は面積を求める計算であると言われています。一方で、積分の計算は微分の逆、とも言われています。本記事では、どうしてそう言えるのかを検証していきます。

ここでの思考の流れは、「積分計算を詳細に分析すると面積計算になることを示す」のではなく、「面積というもの（←敢えて計算といわない）を詳細に分析すると微分の逆になっている＝その計算が積分の計算である」というストーリーです。

わざわざこう書いたのには理由があって、積分するとなぜ面積の計算になるのか、ということを悩むと思考の袋小路に落ちがちだからです。特に数学が苦手な人はドツボにはまります。積分という行為自体がそもそも面積の計算であるので、そこに悩むのではなく、まずは、その面積が、なぜ微分の逆になるのかに注目してほしいのです。

では、それを示してみることにしましょう。

微分の逆とはどういうことか？

まずはおさらいとして、「微分の逆」とはどういうことか、確認しておきましょう。微分というのは元々こういう定義のもの ↓ でした。

ですが、普段は定義を気にすることはあまりなくて、機械的にこういう計算をするものでしたね。

指数関数の数字が x の係数について、指数の数字は一つ減る。そんな計算です。なので、その逆ということは、

ということですが、係数のない x から始める書き方をするなら、

という計算をする、ということになります。これで微分の逆という計算がどういうものかは、なんとなく分かるかと思います。

微分の逆計算が積分（＝面積）であることを示します

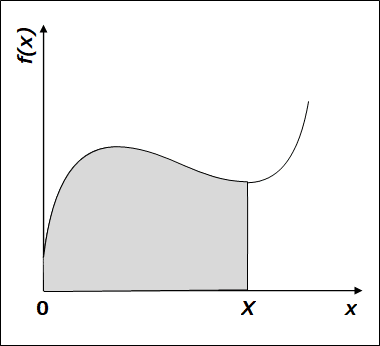
因みに x の関数である f(x) というものが、こんなグラフで書けるとき、

０～X の範囲の定積分は、下の図に示すような面積を指します。

それを表す式はこんな感じに書きます。

この面積は、X の値で変化するものですので、X の関数といえます。という訳で、０～X の間で、図のグレー部分（曲線 f(x) と x 軸が囲む領域の面積）を S(X) と書くことにしましょう。 

この x の範囲が少し広くなって、0～X → 0～X+ΔX に変わる時、面積がどうなるかというと、S(X) → S(X+ΔX) と表現できます。この面積の増分は、図で表すと下の濃いグレーの部分になりますね。

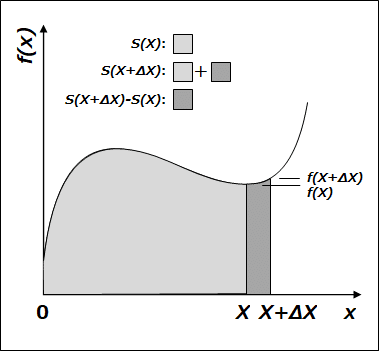
次に濃いグレー部分の面積に近い長方形を、二通りで考えてみます。図のような二つの長方形（破線で図示）です。

この違いは、長方形の縦の長さを、グレー領域の左に合わせるか、右に合わせるか、の違いですが、縦の長さが違うので、面積は別物になります。それぞれ S1，S2 と書くことにしましょう。見た目通り、S1＜S2 です。

この時、両長方形の横幅はいずれも ΔX 、S1 の高さは f(X) 、S2 の高さはf(X+ΔX) です。いずれの長方形も濃いグレーの面積である S(X+ΔX)-S(X) とは異なりますが、その大小関係は見た目から分かります。

長方形の縦横の長さはさっき示した通りなので、S1，S2 を縦×横表記で書くなら、

両辺を ΔX で割ると以下の関係になります。

この差分は ΔX が小さければ小さいほど小さくなり、ΔX→0 の極限でf(X+ΔX)→f(x) 。ということは、その間にある真ん中の式も、

必然的にこうならざるを得ません。数学で「挟みうちの原理」というやつです。これを、極限を表す lim を用いて表すと、以下の書き方になりますね。

お気づきでしょうか。左辺は微分の定義式そのものです。関数 S(X) は、何を表していたかというと、「f(x) と x 軸が囲む領域の面積」と定義していました。で、その面積は、f(x) の積分であるという前提で話をしてきました。

つまり上の結果は、f(x) を積分して求められる S(x) という関数は、微分すると元の f(x) に戻るということを意味しています。

ということは・・・、

積分は微分の逆をする計算である

ということが言えますね。納得いただけたでしょうか？

何か騙されてる気がする人いますか？

ここまでで納得いただけた人はいいんですが、かゆいところに手が届かない感を感じている方もいると思います。多分、その気持ち悪さは、

f(x) の 0～X の範囲の定積分、

が、

上のグラフの「グレーの部分の面積を S(X) と計算できたとして」という前提で話を進めて、結局面積の計算の話には一度も立ち入らないまま、「微分の逆をやれば、積分の計算になって、その計算が面積の計算である。」と示して、話を終わりにしようとしているからだと思います。

だって、面積計算って言ったら縦×横でしょう？そういう議論が一度も出ないで、「はい計算できました！」とか言われても、どことなく騙された感がぬぐえません。一番肝心なところに最後まで触れてない感じです。

というわけで、ここはひとつ、積分と縦×横（＝面積）の関係をはっきりさせておきたいと思います。

面積計算の基本はやっぱり【縦×横】

小学校で習ったように、面積の計算の基本は、やっぱり縦×横です。積分とか小難しい話っぽく感じますが、やっぱり基本的にはどこまでも縦×横を追求する話と思っててください。

しかし、縦×横というのは、正方形や長方形なら簡単に計算できますが、曲線で囲まれた図形の計算は難しくなります。

例えば、こんなの↑の面積を計算するのは難しいですね。

積分の考え方の第一歩は、一緒ではないが大体近い面積を出してみようというところから始まります。上の楕円の場合なら、以下のような計算を試みるのです。

内側に並ぶ長方形の集団は、どれも縦×横で計算できます（ただし、計算できるためには縦と横の寸法は分かってないといけませんが）。
ただ、

は同じものではないので、右側の長方形群の面積を計算しても、楕円の面積を計算したことにはなりません。

でも、

こんな太い長方形で計算する面積よりは、かなりマシなのは分かると思います。つまり、長方形の幅が狭くなればなるほど、楕円の面積に近づくことは間違いないでしょう。積分では、「長方形の幅が無限に狭くなれば、計算結果は楕円の面積に無限に近づく」と考えるのです。長方形の横幅を Δx とするなら、その幅が細かければ細かいほど、楕円との誤差は小さくなります。究極的には、

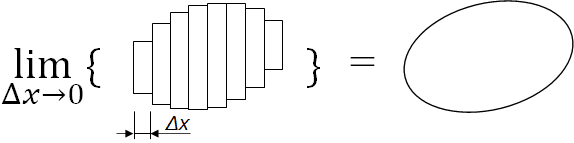
こんなイメージです ↑

この考え方で、先ほどの f(x) が成すエリアの面積を近似的に表すと、こんなイメージになります。

これなら、長方形の幅が小さくなればなるほど、面積の合計は S(X) に近づくイメージが湧きますね。

まあ、イメージがついても計算するには式にしないといけません。

これを数式で表すにはどうしたらよいでしょうか。各長方形の縦と横の寸法が分かれば表現できます。横幅については、0～X の区間を等分するなら、すべて同じ幅にできます。Δx とすることにします。

縦幅はそれぞれの x 座標に対応した f(x) であるはずです。そもそも図の曲線は f(x) を表したものでした。じゃあ、各長方形の右辺の x 座標に名前を付けることにしましょう。こんな感じに↓

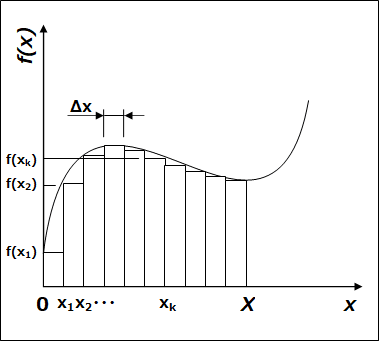
となれば、それぞれの長方形の面積は、左から順に↓ のように書けます。

それぞれ縦×横をやっているだけです。長方形群の総面積は足し算なので、Σ記号を使って書くことができます。0～X 区間を n 分割している場合、長方形の数は n で、

右辺は左辺の近似ですので、「＝」ではなく「≒」で表現しました。これが「＝」で結べるのは、Δx→0 の時です。分割数的には n→∞ です。で、その足し算が面積と等しくなるということですが、その面積は 0～X 区間の f(x) の定積分ということでしたので、

と書けることになります。

ということで、積分計算の中身を具体的に書くとこの ↑ ように書けます。なので、積分においても、基本的にはどこまでも【縦×横】の計算を追求しているだけといえます。

で、∫と dx で挟む理由は？

で、改めて最初に提起した問題に立ち返ってみましょう。

なんで、∫ と dx で挟む書き方をしないといけないんでしょうか？「ルールだから覚えろ」で終わらせることもできなくはないですが、この問題も掘り下げてみましょう。それなりの理由があります。

∫ て、「S（エス）」に似てるなとか、思う方がいたかもしれませんが、実際Sがモチーフです。Sは、sum（合計）の頭文字です。一方、足し算をまとめて表現する Σ（シグマ）という記号ですが、これギリシャ文字ですが、これもアルファベットのSにあたります。

滑らかな曲線で表された曲線 f(x) は、長方形の集合体で近似するとカクカクになります。でも、分割数を増やして、細長い長方形の集合体で表現すれば、形はだんだん曲線に近づきます。

分割数を大きくすると、カクカクの Σ は、滑らかな ∫ に近づくんだと、

という関係なんだと思うと、ちょっと腹落ちした感じしないでしょうか。

一方で、面積計算では

のように、シグマの合算対象（←長方形の縦）に対して、全てに Δx（←長方形の横）をかけていました。この部分も、

という関係があると考えることもできます。Δx は、区間を n 分割した時の幅ですから、n→∞ の時、Δx→0 という関係にあります。つまり、同時に起こります。

ならば、

という関係にある、というふうに捉えることもできないでしょうか。

面積を計算するには、横幅の Δx をかけてやらねばなりません。無限分割の極限においては、それを dx と書くのだと。そう考えると、後ろに dx を付けないといけない気持ちになってくるかと思います。

因みに、f(x) を微分する時、f'(x) と書きますが、正式には、

という表現をします。

「微分とは傾きである」を確認してみた という記事で詳しく書いてますが、

という関係にあることを考えると、さっき示した

という関係は、微分にも同じように言えます。数学的な厳密性はないんですが、理解を深めるための解釈の仕方としては、こういう考え方もありなんじゃないかと思います。

終わりに

改めて「積分」という言葉を見返してみると、「積む」と「分ける」という言葉でできています。長方形の分け方が細かければ細かいほど、オリジナルの図形に近づいていく。その長方形群を積み木のように積み重ねると面積になる。

だから積分というんでしょうかね。