微分とか何の意味あるん？（３）-改稿版

先日、本シリーズの（３）を一応投稿したんですが、何とも分かりやすさに難ありと思えたので、改稿することにしました。

────────────────────────────────────────────────

本記事は、数学の微分シリーズの3回目です。

第1回では、簡単な微分の計算方法を紹介しつつ、なぜこんな意味不明な作業を学校で教わるのか、意味あるの？という問題提起をしました ↓

第2回では、微分でやっていることというのは、傾きの計算なのだ。ということを論じました ↓

書いてみて実感しましたが、分かるように書こうと思っても、微分をわかりやすく説明するのは結構大変です。そこで、これまでの話とこれからの展開を図で示しておくことにします。本シリーズの話の流れはこんな感じです ↓

初回の（１）は、「微分とは何か」のイントロダクション。意味はともかく微分の計算をして見せました。（２）では、微分計算の内容はさておき、「微分の意味は傾きを求めるということなんですよ」という話をしました。

今回は、前半（３）・後半（４）の２回に分け、微分の定義に基づいて、その計算をきちんとやっていきます。結果は（１）と同じになるはずです。

その次の（５）では、

微分の定義＝傾きの計算

となっているのだということを示す回にするつもりです。前置きが長くなりましたが、本題に入りましょう。

微分の定義

改めて、微分とは何か。正式な定義式を見ていきます。こんなです。

(ﾟДﾟ)ﾉﾉ<ｸﾞﾊｧｯ

とかなっている人もいるかもですね。難しそうな数式が出てくるとどうしてもね。lim とか、f(x) とかさ、なんか威嚇されてるような気がしますよね。

ですが気にせず前に進みましょう！

あ、この式を見て全く抵抗感がない方は、もう今回の内容はクリアも同然なので、スルーして（４）に進んでいただければと思います。

こういう難しそうな式にぶつかって心が折れる。数学で挫折する要因て、こういうところにあるかなと思います。そこでちょっと脱線して、折れそうな気持を鼓舞する意味で、数学との付き合う時の精神論の話をすることにします。

精神論1：数学で養える精神

数学と向き合う時に大事なのは、一見難しそうな雰囲気にひるまないことです。（１）で、数学の教え方の悪い例として、「何故と思うな」「心を無にしろ」「やり方を覚えろ」みたいな言葉を皮肉を込めて挙げましたが、「心を無」にするという気構えに関しては、あながち否定すべきではないかもしれません。無意味にひるまないためには重要だったりします。

（もちろん、なぜという疑問を封じ込めるために心を無にするのはダメですよ。）

このひるまない気構えは、数学の問題を解く時に必要という意味もありますが、それ以上に人生を生き抜く力として重要ではないかと思います。私は、数学を学ぶ意義は図太い精神を養うことにあるといっても過言ではない、とさえ思ってます。

手順を踏み、一つ一つ切り崩せば、どんなものでも解ける。それが数学であり、数学以外の世界でも通用する、生きる力の一つです。

精神論２：「分からないこと」との向き合い方

数学で「分からないこと」とぶつかるのは日常茶飯事です。学校（ここでは高校のイメージ）の教科には、分かる分からないの土俵に上がらなくても解ける教科と、分からなければ解けない教科があります。

前者は、現国、古典、英語、地理、歴史（日本史、世界史）、生物
後者は、数学、物理、化学

という感じでしょうか（※賛否あると思います。ざっくりのイメージです）。文系科目のほとんどは、覚えれば良し、読めれば良しなところがあり（本質的には違うと思ってますが）、理屈を理解して解くタイプではありません。これに対し、（覚える系の生物を除く）理系の科目は、理屈が分かっていないと全く問題が解けません。

理屈とか、原理とかというものは、理解しないと使えない。その最たるものが数学と言えましょうか。数学と向き合う労力のほとんどは「分からないことに向き合う訓練」ともいえます。

「分からないこと」「できないこと」を乗り越える時に必要なのは、言語化です。漠然と「分からない」と訴えるのではなく、どの部分が分からないかを言葉にすることが重要です。これは生きる力に通ずる能力で、学生時代に限らず、社会に出てからも生涯必要になります。

例えば、営業の仕事をしている人がいるとします。受注を取れず営業成績が上がらない。誰かにアドバイスをもらおうという時に、「どうやったら営業成績が挙げられますか？」という聞き方しかできない人は、多分アドバイスをもらっても自分の力にできません。

その人は、できないことを言語化できていないので、仮にアドバイスで一歩前に進んでも、次の問題にぶつかればまた対処方法が分からないからです。

一方、受注が取れない原因を考え、例えば、「自社製品の強みが生きる業界をどうやったら絞り込めるのか」とか、「競合との値下げ競争になって負けることが多いが、値段以外の方法で戦うやり方は何かあるか」など、自分の問題を言語化できる人には、もらったアドバイスをもとに成長が見込めると思います。

数学はその生きる力を鍛えてくれるといえます。

例えば、微分の定義式を見てやべぇと思ったとき、そのヤバい内容を言語化できるれば、そのハードルを越えるのは、大して難しくありません。例えば、こんな感じでしょうか。

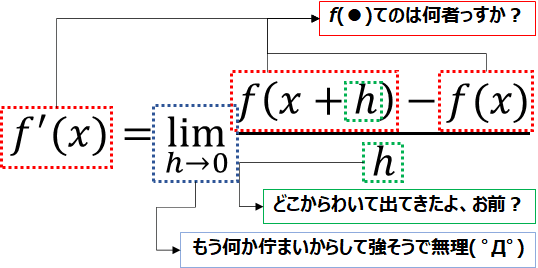
この例では、「無理 ( ﾟДﾟ)」とか言って、思考停止してるところもあり、決して高度な言語化ではないですが・・・、少なくとも式のどの部分が分からないのか、３つの問題に分解していることは重要です。

漠然とわからないといっているだけでは、アクションにつながりませんが、３つの問題に分解していれば、１つずつ対処していけばよい、と先の見通しが立ちますね。

ここで挙げた3つ問題点のうち、lim については、（２）ですでに登場済みです。恐れることはありません。「lim の後ろの式の h の値を0にした時の計算だよ」と思っとけばOKです。

で、h ですが、この由来は後々のこともあるので、（５）で説明したいと思います。

という訳で、今回の残りの記事では、f(x) とは何を意味するかというところだけ、説明しておくことにします。

f(x)というのは何者？

あまり深く考える必要はありません。今まで y=ax2+bx+c とか書いていた式の、y を f(x) と書きかえただけです。書きかえただけですが、書き方に2点の変更点があることには、少し注目しておきましょう。

１．y → f に変更
２．後ろに (x) というのが付いた

1点目は、単に名前の話なので f を使わないといけない理由はありません。ただ、関数（function）という概念を明確に示したい意味で、f という表記に変えるのです。functionの頭文字の f を使用したというだけですね。

関数という用語が登場しましたが、これはある変数を用いた計算式のことを言います。「変数の値が決まれば関数の値も決まる」ということを念頭に入れておけば、充分な理解と思います。

次に2点目の (x) について。これは、「関数 f の変数は x ですよ」という意味です。関数は必ず変数を抱えていますが、その変数が何なのかを明確にすることができます。

加えて、x に値を代入した時、f の計算を分かりやすくする便利機能もあります。例えばこんな感じに使います。

という式に、 x=0 を代入してf(x) を計算するとき、

こういう書き方ができます。（）の中の値が、x に代入された値です。こういう書き方にすれば、いちいち「x＝0 の時」とか、断り書きをしなくても分かるので、便利ですよね。

まとめ

今回は、微分の定義に基づいて、微分計算をする回の前半でした。定義を示し、式の少しわかりにくい（かもしれない）部分を解説しました。

次回は、実際に定義に基づいて微分の計算を行い、（１）で公式を使ってとりあえず計算した結果と一致することを確認します ↓

この記事の上位テーマは ↓ です。よかったらアクセスしてみてください。

削除してもいいんですが、折角なんで残しておきます。旧（３）の記事 ↓