【MCMC法シリーズその1】MCMC法の概要とメトロポリス法

こんにちは。スキルアップAI編集部です。

今回はマルコフ連鎖モンテカルロ (Markov Chain Monte Carlo: MCMC) 法について触れていきたいと思います。機械学習の重要性が日に日に増しているため、この手法の名前を一度は聞いたことがある方も多いのではないでしょうか。MCMC法は乱数を用いて、確率分布を近似的に計算する手法であり、多くの場面で利用されています。

本記事ではMCMC法の基礎的な内容についてまとめた後、MCMC法の手法の1つであるメトロポリス法について、直感的に理解できるように説明をしていきたいと思います。

1.MCMC法の概要

統計分析では、パラメータの事後分布を推定する際に、MCMC法がよく用いられます。事後分布は以下のようなベイズの公式で表される確率分布です。

ただし、 θ はパラメータで、 D はデータを表しています。この計算では、右辺の分母のようにパラメータの積分計算が必要となりますが、しばしばこの積分計算自体が困難な場合があります。そのため、この計算を行う際に、MCMC法はとても有効な手法となります。

MCMC法は「マルコフ連鎖」と「モンテカルロ法」の2つの概念の組み合わせた単語です。したがって、「マルコフ連鎖」と「モンテカルロ法」を切り分けて説明していきたいと思います。

2.モンテカルロ法とは

モンテカルロ法は、「乱数を用いて近似計算を行う手法」のことです。有名な例として、モンテカルロ法を用いて円周率を近似計算する方法が挙げられます。この方法を説明します。

まずは図1のように、辺の長さが2である正方形の中に半径が1の円を考え、この正方形の中でランダムに点を打っていきます。

図1:正方形内に点をランダムに打ち、
モンテカルロ法を用いて円周率を求める。

基本的な考え方は、円の領域に入った点の個数は、領域の面積に比例するというものです。すなわち、

と考えます。ただし、 X は円内の点の個数で、 N は打った点の総数です。また、 右辺は面積比です。もう少し確率的な観点で説明すると、1点が円内に入る確率は、(円の面積)／(正方形の面積)で考えられます。この確率は

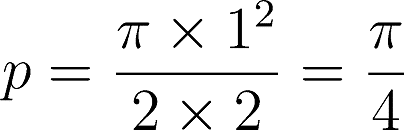
となります。そして「大数の法則」により、円内に入った割合 X／N が、点数が増えるに連れて、 π／4 へ収束していくと考えることができます。

図2では、N（打った点の総数）を増やした結果を表しており、点の個数が増えるほど3.14…に近づいていることがわかります。

図2:モンテカルロ法でランダムに点を打った結果と円周率の結果

点数 N が多いほど3.14…に近づいている結果が得られます。 ただし、赤線は半径1の円、緑はランダムに打った点を表します。

3.マルコフ連鎖とは

マルコフ連鎖は、「未来の状態は、現在の状態だけで決まり、過去の情報は影響しないという考え方」を意味します。
マルコフ連鎖を数式で表現すると以下のようになります。

この式の意味を簡単に述べると、ある時刻 t+1 の状態 Xt+1 は、その直前の時刻の状態 Xt だけによって決まり、 Xt より前の状態は影響しないということです。例えば、天気の統計モデルを考える際、ある日の天気を決めるのはその前日の天気だけと割り切り、2日前以前の天気の影響は無視します。

この仮定を導入することで考慮すべき変数が減り、モデルを組み立てやすくできるというメリットがあります。また、この式のことを「遷移確率」と呼ぶこともあります。

4.MCMC法の一例 : メトロポリス法

これまで説明してきた「モンテカルロ法」と「マルコフ連鎖」を組み合わせたのが「マルコフ連鎖モンテカルロ (MCMC) 法」です。すなわち「直前の状態だけを考慮しながら、乱数を用いて近似計算を行う」という方法として理解できます。

このMCMC法の具体的なアルゴリズム例として、「メトロポリス法」を紹介します。この手法はMCMC法の中でも、最も基本的な方法です。ある確率密度関数 f(x) に対して、以下の流れで f(x) の点列を算出します。

1. 初期値 θ(t=0) を決めます。
2. 次の地点の候補点 θ(a) をランダムサンプリングします。
3. f(θ(t)) ＜ f(θ(a)) の場合はパラメータを更新 (θ(t+1) ＝ θ(a)) します。
   対して、 f(θ(t)) ＞ f(θ(a)) の場合は以下のルール a. で決めます。

この方法は「山登り」に例えることができます。山を確率密度関数 f(x) とした場合、山頂に向かってひたすら登り、山頂付近ではなるべく留まろうとする登山者の動きとしてイメージできます。

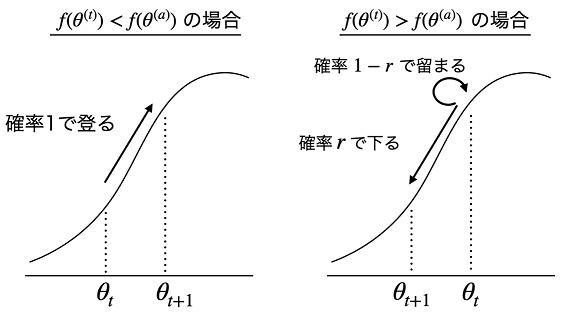
図3:メトロポリス法のサンプリングのイメージ図

確率密度関数の高い位置になるべく長くいることで、確率が高い部分を重点的にサンプリングすることに繋がります。

5.まとめ

本記事ではMCMC法の基礎的な概念についてまとめ、基本的な手法の1つであるメトロポリス法について紹介しました。MCMC法の大まかな計算の流れは以下の通りです。

MCMC法の手順の大まかな流れ

1. パラメータを θとし、その初期値 θ(t=0) を定めます。
2. ある規則に従って、パラメータの候補値 θ(a) を得ます。
3. 現在のパラメータを更新するか (θ(t+1) ＝ θ(a)) 、もしくは更新しないか (θ(t+1) ＝ θ(t)) を確率的に決定します。
4. 2 と 3 の操作を一定回数繰り返します。

この 2 と 3 の部分の違いによって、様々な手法が提案されています。
今回はメトロポリス法だけ紹介しましたが、次回の記事ではハミルトニアンモンテカルロ (Hamiltonian Monte Carlo：HMC) 法という、より高度な手法について紹介します。

6.参考文献

[1] 学びTimes : 高校数学の美しい物語 モンテカルロ法と円周率の近似計算、(2021年)
[2] 豊田秀樹 : 基礎からのベイズ統計学 ハミルトニアンモンテカルロ法による実践的入門、朝倉書店 (2015年)
[3] 涌井良幸、涌井貞美 : 身につくベイズ統計学、技術評論社 (2016年)

☆☆☆
スキルアップAIのメールマガジンでは会社のお知らせや講座に関するお得な情報を配信しています。
配信を希望される方はこちら

また、SNSでも様々なコンテンツをお届けしています。興味を持った方は是非チェックしてください♪
Twitterはこちら
Facebookはこちら
LinkedInはこちら
スキルアップAI公式YouTube AIビジネスチャンネルはこちら