
Sports Biomechanics Geek #11 〜多関節運動の代表値 多体系における瞬間回転軸の意味〜
剛体運動とは並進と回転の合成のことである.また並進と回転は,座標系の取り方によって変化する.このことが,剛体の運動をわかりにくくする理由の一つである.この問題を解決する方法の一つとして,特別な座標系から記述する,瞬間回転軸や力の作用線による表現がある.瞬間回転軸は剛体の運動を一つの回転軸で記述し,力の作用線は一つの回転の力(力のモーメント)で剛体の力学を記述する.このときの回転の軸や作用線の位置が,剛体の運動と力学を象徴し,剛体の運動の変化を敏感に示し,運動の意味をわかりやすくする効果がある.瞬間回転軸と力作用線についてはすでに述べたが,ここでは,特に瞬間回転軸が多体系の力学でそれらがどのような意味を持つのかをもう少し詳しく述べていく.
はじめに
バイオメカニクスの分析といえば,物理量として速度,加速度,角速度,関節に作用するトルクなどで分析することが多いだろう.これらは身体各部位の特徴を表す基本的な物理量だが,身体運動の本質的な物理的意味を見いだしにくい.時系列グララフを見て,どのような事が起きているか直感的に理解することは難しいだろう.
バイオメカニクスではあまり馴染みないが,これまで述べてきた曲率中心,瞬間回転軸などのを用いることで,運動の本質的な意味は見いだしやすくなることをこれまでの記事で述べた.特に3次元空間に可視化した際にも直感的に理解しやすい点もあるが,運動の違いがそれらの特徴量の変化として顕著に現れる.
剛体の瞬間回転中心や力の作用線は,対象となる剛体の運動だけに関係するという印象を与えるが,それが身体のような多体系でどのような意味を持つか考えていきたい.
ここでは,ゴルフとバットのスイング運動の解析例に加えて,スポーツではないが瞬間回転軸等を全身運動の解析に応用した研究も紹介する.ただし,この研究はドライバーの全身の運動解析を行ったものだが,スポーツのような運動の解析でも,同じような分析を行うことは面白いだろう.
瞬間回転軸
軸の位置(ゴルフスイングの例)
瞬間回転軸(ISA, instantaneous screw axis)は,「軸」なので,3次元空間において,その軸が通る位置と,軸の方向で構成される.軸の方向は剛体の角速度ベクトルで定まるので,ISAを用いて解析する意味は軸が通る位置を示すことである.軸の方向を知りたいだけなら,剛体の角速度ベクトルを計算するだけでよいのだから.
なお,剛体の瞬間回転軸が,その剛体から離れるほど,回転の中心が遠くになることを示している.たとえば

では,ゴルフクラブの瞬間回転軸の変化の様子を示した(図1).ただし,この角速度はクラブのシャフト軸まわりの回転を無視している角速度で,図のクラブに示した線だけの角速度という言い方ができる.クラブの先端の接線速度だけで定めた角速度である(補足1).
これを
$$
\bm{\omega}_{xy}
$$
と記述する.補足1に示したが,クラブに固定した座標系で,シャフト軸方向を$${z}$$方向として,それに直交する方向が$${x,y}$$方向という意味である.
このスイングにおける,ゴルフスイングのダウンスイング開始からスイングの前半(黄色い線まで)は,左右の肩の中心付近にあり,次第にインパクトに近づくにつれて,手首の近くに移動していることがわかる.
このことはダウンスイング最初は,腕とクラブは比較的一体化されており,腕の運動を中心に回転させて,後半は腕の運動が弱まり,クラブの遠心力によって自然と回転していることを示している.
角速度ベクトル(軸)の合成
繰り返しになるが,瞬間回転軸は3次元空間において,その軸が通る位置と,軸の方向で構成されることになるが,回転軸は角速度ベクトルそのものである.
すると軸は角速度ベクトルなので,その角速度ベクトルを分解することもできる.
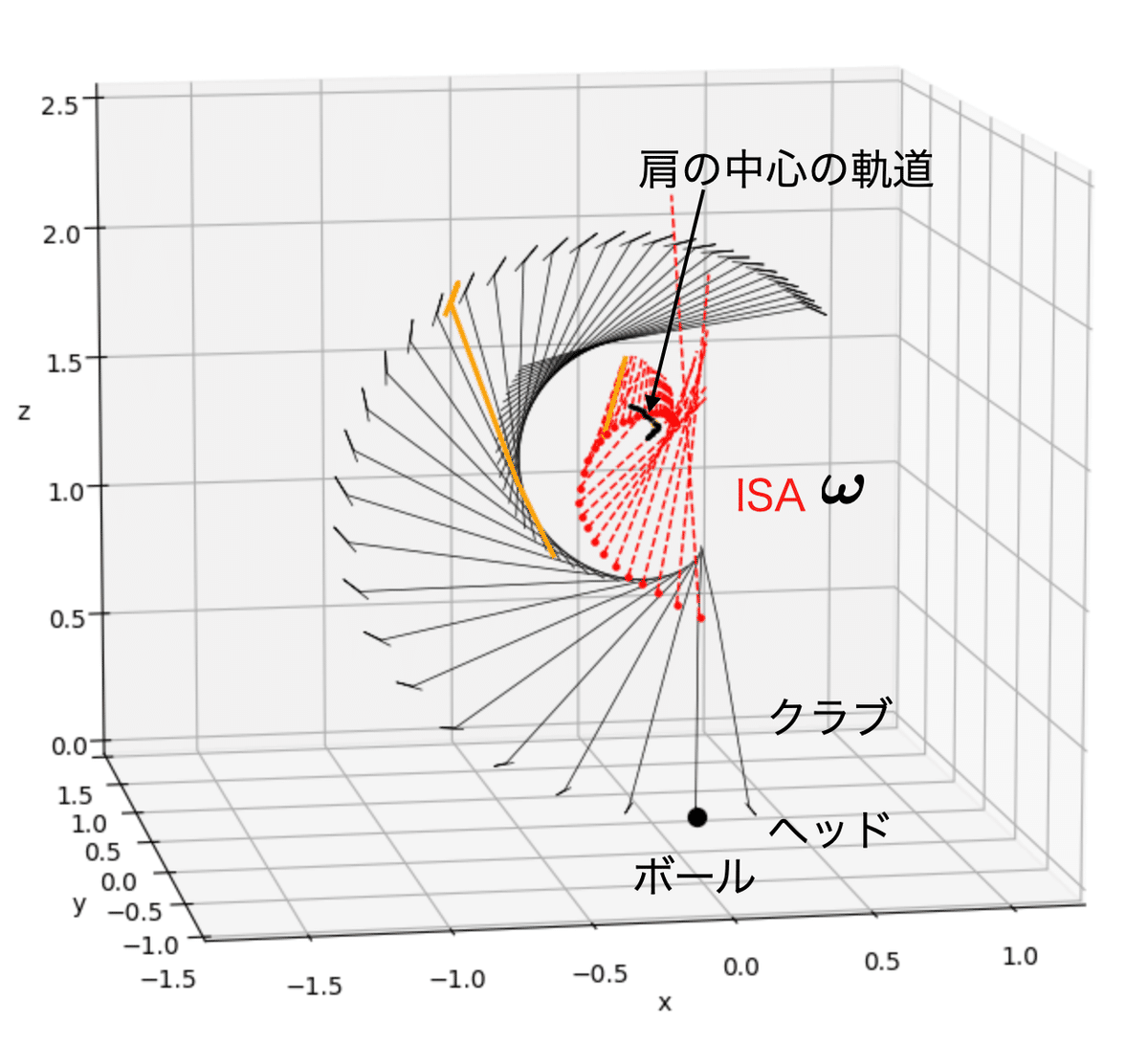
図2は図1の角速度にさらに,シャフト軸まわりの回転を加えた角速度ベクトルを描いている.これは通常の剛体の角速度ベクトルである.クラブのスティックピクチャにもヘッドの向きを書き加え,シャフト軸回転の様子をわかるようにした.
このクラブの角速度ベクトルはシャフト軸まわりの回転を含んでおり,
$$
\bm{\omega}
$$
と記述する.

すると,先ほども述べたように,角速度ベクトルは合成できるので
$$
\bm{\omega} = \bm{\omega}_{xy} + \bm{\omega}_z
$$
のように,クラブの角速度ベクトル$${\bm{\omega}}$$(赤)は,シャフト軸まわりの回転を除いた角速度ベクトル$${\bm{\omega}_{xy}}$$(緑)+シャフト軸まわりの角速度ベクトル$${\bm{\omega}_z}$$(青)で記述することができる.
これを拡大して示したのが,図3である.
図1も図2も特徴が異なるので,解析の内容によって使い分けるとよいだろう.図1ではゴルフスイング中,シャフト軸回転を除けば,ほぼ同じ軸方向を向いていることから,連続したクラブの線で構成される,「スイングプレーン」がほぼ平面に近いことを示している.ゴルフ用語で「オンプレーン」の状態にあることを示している.
図3の$${\bm{\omega}_z}$$(青)は,インパクト前に急速なシャフト軸回転が起こっていることを示している.フェースの向きは,徐々にではなく,図2のフェースの面を観察してもわかるが,かなり直前に調整されていることを示している.なお,図3の青線はわかりにくいが,プレーンに沿った,すなわち緑の線に直交する方向のベクトルであることに注意をされたい(そのようには見えないが,3Dの視点によってわかりにくくなる).
さて,このような情報はスティックピクチャを見ても,グラフを見てもわかりにくいだろう.運動を直感的に理解するうえで,瞬間回転軸は大きな効果があることがわかるだろう.
なお,図1の「軸の通る位置」は,シャフト軸まわりの回転を無視した角速度ベクトル$${\bm{\omega}_{xy}}$$で定めた軸の位置で描いており,図3はシャフト軸まわりの回転を含めた角速度ベクトル$${\bm{\omega}}$$で定めた軸の位置を描いているので注意をされたい(補足1参照).
ゴルフスイングの場合,クラブの瞬間回転軸の方向,すなわち角速度ベクトルは図3左のように,シャフト軸まわりの角速度を除けば,ほぼ同じ方向を向く.ただし,ここで,軸方向の運動は考慮していない.

つまり,仮に,軸方向がスイング中完全に同一方向を向いていたしても,軸方向に速度を持つ場合がある(図4).その場合,シャフトが構成する平面は完全な平面になるとはかぎらない.
実際,スイングプレーンは下方に移動しながらダウンスイングするケースが多い.
なお,図1〜4の軸の始点(軸の一番下側の点)は,グリップ部から最も近い位置にISAの点を定めている.
バッティングの場合

ゴルフスイングの場合,クラブの瞬間回転軸の方向,すなわち角速度ベクトルは図3左のように,シャフト軸まわりの角速度を除けばほぼ同じ方向を向いているが,野球のバッティングではやや事情が異なる.
図5は,ゴルフ同様にバットスイング時のバットのスティックピクチャと瞬間回転軸(ISA)$${\bm{\omega}_{xy}}$$を描いたものである.軸の角度や軸を通る位置は,選手によってかなり異なる.図5の例は比較的一定の軸方向を示しているが,前半は少し傾き(水平に近い方向),後半は鉛直方向に近づいている.また,選手によってこの軸の通る位置も様々で,選手の特徴をISAはかなり反映する.
なお,スイングを加速させようと考えると,ダウンスイングの前半はバットにエネルギーを注入させたいので,地面と蹴り合いを考えると力が作用する方向は上下方向となるため,グリップ位置を比較的上にした状態から下向きにスイングする傾向にある.このときISAの軸方向は傾き水平方向をに近づく.また,ゴルフスイングと異なり,身体全体の並進運動を含み,剛体の並進運動は半径を大きくするので,軸の位置は身体からかなり遠い位置から移動することもある.
しかし,スイングの後半は,筋力でバットを加速させることは困難な状況にあり,自然にバットが加速する状態であり,ボールに当てることが重要となるので,ISAの軸は上下方向に近づく傾向にある.
ただし,プロ野球選手では,プロのゴルフスイングよりはかなりバリエーションがあり,上記のような傾向に当てはまらないスイングを行う選手も多いことには注意されたい.
しかし,バリエーションは多いが,この軸方向が一定であることが良い傾向であるとされているようだ(オンプレーンの効率).最近の報道でも注目されており,物理的にも合理的な考え方であると筆者も考えている.
おそらくオンプレーンとはバットの軌道から算出し,瞬間回転軸はその速度から計算するもので,それら対となる考え方であるが,細部において異なるので,詳しい定義は
を参照されたい.
多体系における瞬間回転軸の意味
ここでは,クラブやバットのように末端の剛体の運動の瞬間回転軸を観察しているが,異なる運動で,末端の隣の部位(剛体)の」瞬間回転軸を観察した研究例(文献1)を取り上げよう.

図1,2の軸はダウンスイングの前半,首のあたり(左右の肩の中心に相当)にあり,腕とクラブが一体化し,左右の腕を回すことで,クラブを回していることを示していた(図6).

これに対して文献1では,運転中のドライバーの胸郭(体幹上部)の瞬間回転軸が,身体のどの部位を貫いているかを調べている.運転中,胸郭の瞬間回転軸は頭部の重心近くを通っている.このことは,運転中,ドライバーは頭部を動かさないように制御していることを示している.
おわりに
ここでは,剛体の瞬間回転軸が多体系の力学でどのような意味を持つのかについて述べた.
瞬間回転軸は運動の特徴をよく反映し,3次元空間で可視化することで,その意味を捉えやすくし,個性をよく反映する.
また,その軸の方向もさることながら,軸が通る位置を知ることで,どのような制御を行っているかも知ることができる場合がある.ゴルフでもバッティングでも,スイングの前半では,クラブやバットの瞬間回転軸は体幹近くに位置し,次第に手首に近づいていることは,それらの制御が体幹側から次第に手首側に移動していることを示していた.
ドライバーの運転では,頭部を動かさないように制御していることが,隣の胸郭の瞬間回転軸を解析することでわかった.
このように,剛体の瞬間回転軸はその剛体自身の制御だけでなく,多体系の運動でどのような制御を行っているかを示すことができる.
参考文献
1)羽田ら,瞬間回転軸と作用線を用いたドライバ人体挙動の可視化,自動車技術会論文集,Vol.46, No.1, pp 161-166, 2015.
補足
補足1:線の角速度ベクトル

本来,剛体の角速度ベクトルは3次元の情報を持つ(図8左).しかし,バットやゴルフクラブを,グリップエンドとバットやクラブの先端の二点を結ぶ線として記述する場合は,バットやクラブの長軸まわりの回転を記述できない(図8右).モーションキャプチャなどで計測する際に,何らかの事情でその二点しか得られないこともあるだろう.
そのような線の三次元運動の角速度ベクトルを算出することを考える.
角速度ベクトル$${\bm{\omega}}$$は
$$
\bm{\omega} = \bm{\omega}_{xy} + \bm{\omega}_z
$$
のように,長軸まわりの角速度ベクトル$${\bm{\omega}_z}$$と,それに垂直な平面($${x,y}$$で張られる平面)内にある角速度ベクトル$${\bm{\omega}_{xy}}$$との和で記述できるが,図8の右の場合は,角速度ベクトル$${\bm{\omega}_z}$$が不明であるが,長軸まわりに回転していないと便宜的に仮定すれば,バットの角速度ベクトルとして,$${\bm{\omega}_{xy}}$$で算出することも可能だ.
そこで,ここでは長軸まわりの回転を無視した角速度ベクトル$${\bm{\omega}_{xy}}$$を算出する方法を考える.

ここでは,三次元空間内の角速度ベクトルとして$${\bm{\omega}_{xy}}$$を計算する方法を示す.ここでバットの先端の位置ベクトルを$${\bm{x}_h}$$,グリップエンドの位置ベクトルを$${\bm{x}_g}$$とすると,並進運動を除いたバットの「回転だけによる」バットの速度ベクトルを$${\bm{v}_b}$$とすると
$$
\begin{aligned}
\bm{l} &= \bm{x}_h - \bm{x}_g\\
\bm{v}_b &= \dot{\bm{l}}\\
\end{aligned}
$$
から得られる.
しかし,角速度ベクトル$${\bm{\omega}_{xy}}$$は,$${\bm{l}}$$と$${\bm{v}_b}$$にも直交する.また,
$$
\begin{aligned}
\bm{v}_b &= \bm{\omega}_{xy} \times \bm{l}
\end{aligned}
$$
の関係も満たす.そこで,$${\bm{\omega}_{xy}}$$の向きは,$${\bm{l}}$$と$${\bm{v}_b}$$に直交する方向なので,$${\bm{\omega}_{xy}}$$の軸方向の単位ベクトルは
$$
\begin{aligned}
\bm{e}_{xy} = \frac{\bm{v}_b \times \bm{l}} {{|\bm{v}_b \times \bm{l}|}}
\end{aligned}
$$
によって算出される.また,その大きさは
$$
\begin{aligned}
\bar{\omega}_{xy} = |\bm{\omega}_{xy}| = |\bm{v}_b|/|\bm{l}|
\end{aligned}
$$
で記述される.以上から,長軸まわりの角速度を除いた,線の運動の角速度ベクトル
$$
\begin{aligned}
\bm{\omega}_{xy} = \bar{\omega}_{xy} \bm{e}_{xy} = |\bm{\omega}_{xy}| \bm{e}_{xy}
\end{aligned}
$$
を計算できる.
なお,もし,反対にIMUのジャイロセンサで三次元でフルに角速度ベクトルを計測できる場合は,長軸方向の角速度成分を0とすればよい.



【著作権・転載・免責について】
権利の帰属
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
【データの計測について】
スポーツセンシング社のスタジオで,フォースプレートやモーションキャプチャを利用した計測も行えます.出力されるデータと,ここで示したプログラム(入力データの取り込み関数を少々改変する必要があるが)で,同様な解析を行えますので,まずはお気軽にお問い合わせください.
