モーションにおける３次元回転 #11　〜加速度・角速度信号の座標変換〜

モーションセンサ（IMU，慣性センサ）で計測する加速度や角速度はセンサに固定されたローカル座標系の信号として計測され，モーションキャプチャは絶対座標系の位置情報を与える．また，身体運動の解析，特に力学計算では最終的には座標系を統一されて計算されるが，その計算過程ではそれらが混在するので，ローカル座標系と絶対座標系間の変換が必要となる．

これまで，回転行列をその名の通りベクトルを回転させる行列としてその意味を述べてきた．そこでは有向線分としての幾何ベクトルを中心とした議論であった．この場合，座標系や成分を意識することなく，有向線分のように矢印としてのベクトル，すなわち3次元空間の中で方向と大きさだけを考えればよく記号でも

$$
\bm{a}
$$

のように成分の表れない記号で考えればよいだけである．数学的な議論を行うときには，わざわざ成分を持ち出す必要はない．そのほうが座標系や回転角度パラメータの不連続など，多くの面倒な問題から開放される．

しかし，いざ計測という段階になると，回転に関する計測データは嫌でも成分として与えられ，それは座標系と紐付いたデータとして出力される．

そこで，ここでは有向線分としての幾何ベクトルではなく，ベクトルの成分まで考え，その成分を異なる座標系で表す際に必要となる「座標変換としての回転行列」について考える．

回転行列と座標変換行列

ここでは，ローカル座標系で観測された信号を絶対座標系の信号に変換する時のように，信号であるベクトル自体は回転させず，座標系を回転させて信号を観察することを考える．

このような座標系の回転によって，ベクトルを見る視点を回転させることを座標変換と呼ぶ．以下に回転行列と座標変換の関係をまとめる．

図１：（a）ベクトルの回転と（b）座標変換

まず，ベクトルの回転と座標変換の関係を１自由度の回転で考える（図１）．(a)ではベクトル$${\bm{a}=[a_x~a_y]^T}$$を$${-\theta}$$だけ回転させて，$${\bm{a}'}$$に移動してするベクトルの回転を示している．一方(b)では，座標系$${\Sigma_x}$$を$${\theta}$$だけ回転させて，新しい座標系$${\Sigma_{x'}}$$から同じベクトル$${\bm{a}}$$を観察する．ただし，このとき，(a)と(b)の回転量は同じ$${\theta}$$だが向きが反対となる逆回転であることに注意されたい．

(b)の新しい座標系$${\Sigma_{x'}}$$のもとでのベクトル$${\bm{a}}$$の成分を$${\bm{a}' = [a'_x~a'_y]^T}$$とすると，実は(a)の回転後のベクトル$${\bm{a}'}$$の成分と，(b)の座標変換後の新しいベクトル$${\bm{a}'}$$の成分は一致することが図からも読み取れる．つまり，回転行列が直交行列であるため座標変換行列はベクトルを回転させる回転行列の逆関数，すなわち転置行列

$$
\bm{R}^{-1}(\theta)=\bm{R}^T(\theta)=\bm{R}(-\theta)
$$

となっている．これらの関係は１自由度の回転で成り立ったが，一つの回転軸と回転角度で記述できるというオイラーの定理からも，３次元回転でも同様の関係

$$
\bm{R}^{-1}(\bm{n}, \psi)=\bm{R}^T(\bm{n}, \psi)=\bm{R}(\bm{n}, -\psi)=\bm{R}(-\bm{n}, \psi)
$$

が成り立つ．ここで，$${\bm{n}}$$はロドリゲスの式の回転軸，$${\psi}$$は回転角度である．なお3次元で姿勢を回転行列で表す場合，行列は姿勢と1対1に対応し不連続も発生しないが，それをロドリゲスの式で表す場合，回転軸$${\bm{n}}$$か$${\psi}$$のどちらかを反転することで，逆回転を表すことができる．つまり1対1ではなく，二通りの解があることに注意されたい．

このように回転行列と座標変換行列の間の関係は，表裏一体で，それらは転置行列で行き来できる．

絶対座標系への変換

図２：加速度信号（重力加速度）のセンサ座標系への分配

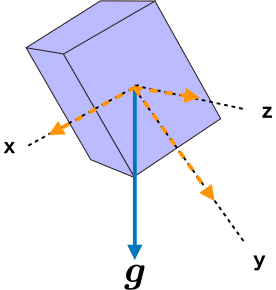
ここでは，モーションセンサをその場でゆっくり回す作業を考える．ゆっくり回す理由はモーションセンサの加速度信号として，並進加速度や向心加速度などの他の加速度をできるだけ観測させずに，重力加速度だけを検出させるためである．

ここで，モーションセンサを有限回転させるなら，センサは絶対座標系で観察した重力加速度ベクトル$${\bm{g}_g=[0~0~-g]^T}$$を「センサに固定された座標系に座標変換」した信号$${\bm{g}_s}$$として出力することと等価になる．つまりこの実験の場合，重力加速度ベクトル自体は常に下向きで固定されており，回転しているのは観測するセンサの座標系で，前述の結果からセンサは$${\bm{R}^T \bm{g}_g}$$の計算を通して「センサ座標系」に変換された重力加速度$${\bm{g}_s}$$を出力し，図２のように重力加速度1Gを$${xyz}$$の各成分に分配して出力していることになる．

そこで，次にセンサ座標系$${\bm{a}_s}$$で計測された加速度をもとの絶対座標系の加速度$${\bm{a}_g}$$に戻すにはセンサ出力の加速度$${\bm{a}_s=[a_{sx}~a_{sy}~a_{sz}]^T}$$に対して，$${\bm{R}^T}$$の逆回転である$${\bm{R}}$$をかければよいので ，モーションセンサの出力である単位クォータニオン$${\bm{q}}$$から計算した回転行列$${\bm{R}(\bm{q})}$$（７章