【素数筆算】素数を重ねて素数を作ろう(たしざん編)

今回は、素数を2つ使って新しい素数を作ろうというコーナーです。

といっても、難しい手続きが必要なものだと面倒です。そこで思いついたのが、筆算。

そろばんをやっている方は筆算をしないと思いますが、学校では以下のような筆算を学びますよね。

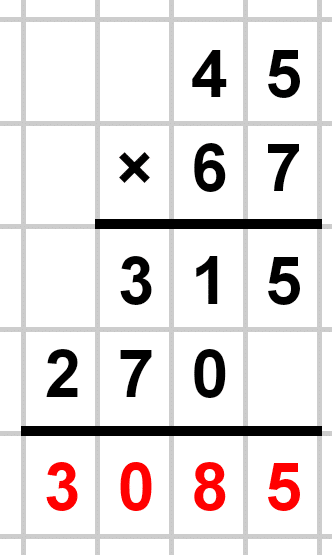
そこで、素数を使ってこの形と同じように筆算をしていこうと思います。

ただ、作るには条件が必要です。素数は無限に存在するので、ある程度制約を設けて作った方がいいかなと…。

そこで考えたのは、

①連続する素数同士で筆算をします。

さらに、

②2つの素数の差が6の倍数のものを使います。

②を作った理由は必然。差が6の倍数でないと、筆算したときに3の倍数になってしまうからです。

例えば、双子素数の(11, 13)は差が2です。これらで筆算をすると、

141=3×47

となるので、3の倍数になってしまうのです。

詳しい説明はここでは省きますが、

2つの素数p, qの差が2や4の場合、2つの素数p, qを3で割った余りは1と2になります。1と2を足すと3になってしまうので、筆算で足し合わせると3の倍数になるんですね。

わからない方は、色々な数についても試してみて、理解を深めてみてください。

さあ、

①連続する素数同士で筆算

②素数の差が6の倍数のものを使う

この①②を満たす素数たちで筆算したらどういう結果になるのか見ていきます。

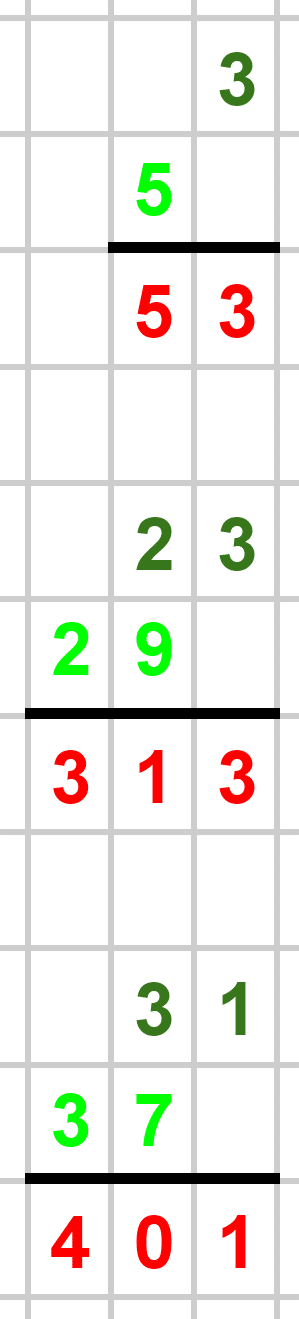
赤い数字で計算結果を示しましたが、なんと素数ばかり…！すごいですね笑。

SOSU !

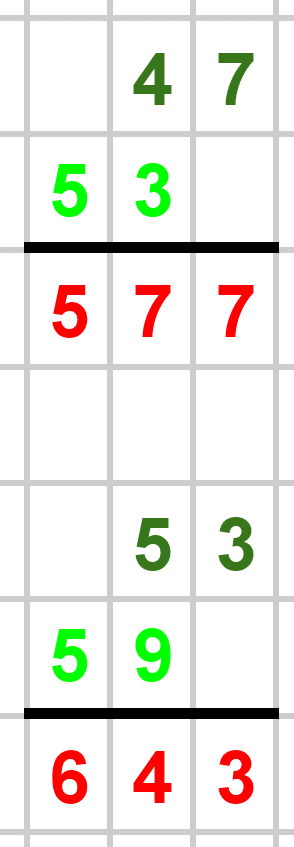
これがずっと続くと思いきや…

素数でないケースも当然ありました。世の中、そんなに甘くないですね笑。

実際は、もっと大きい数で試すと素数でないケースがたくさんありました。興味のある方はページ下の「★付録★」をご覧ください。

今回は、初めてこのような素数による筆算を試してみました。

意外と素数が作れる一方、一見素数に見えるけど素数でない数もたくさん発見しました。今回のような試行錯誤は今後も続けていこうと思います。

素数はいつも、あなたのそばに。
Let's enjoy SOSU !

最後まで読んでいただき、ありがとうございました。

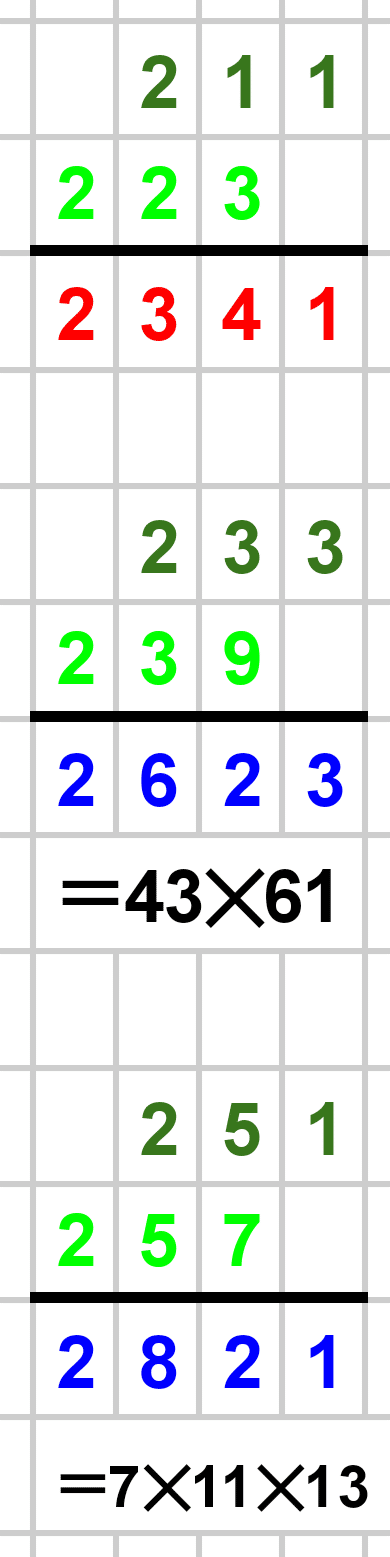
★付録★

1000以下の素数たちによる筆算結果を以下に載せておきます。赤が素数、青が素数でない数です。素数でない場合は素因数分解も書きました。暇な方はじっくりとご覧ください！

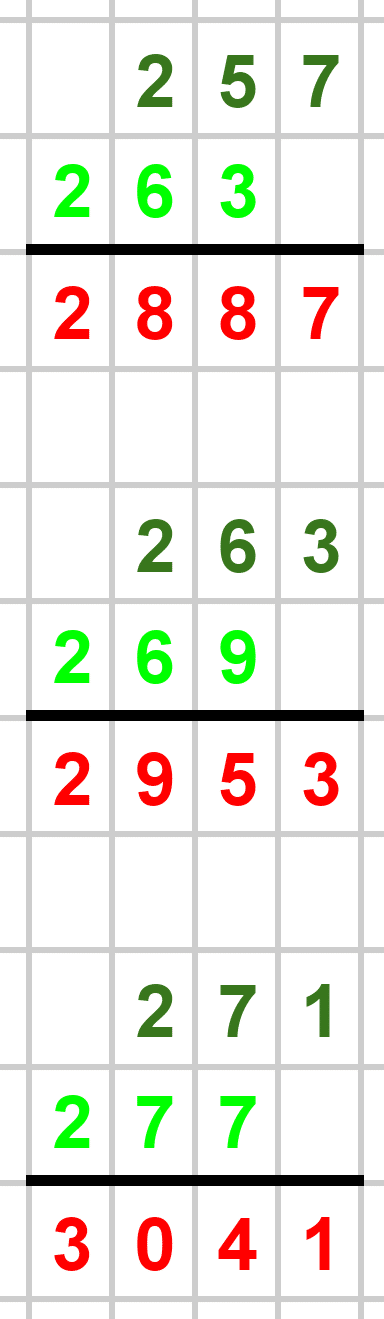
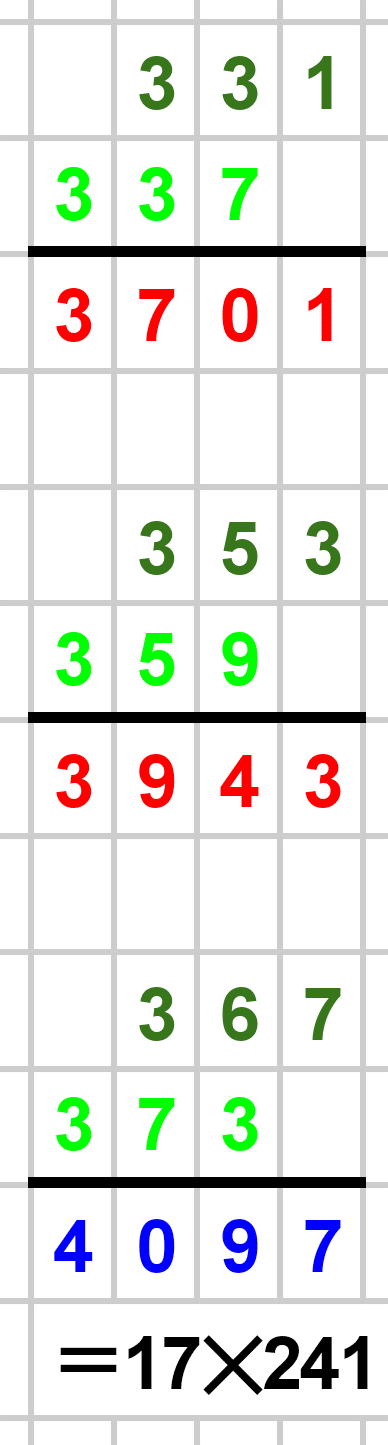
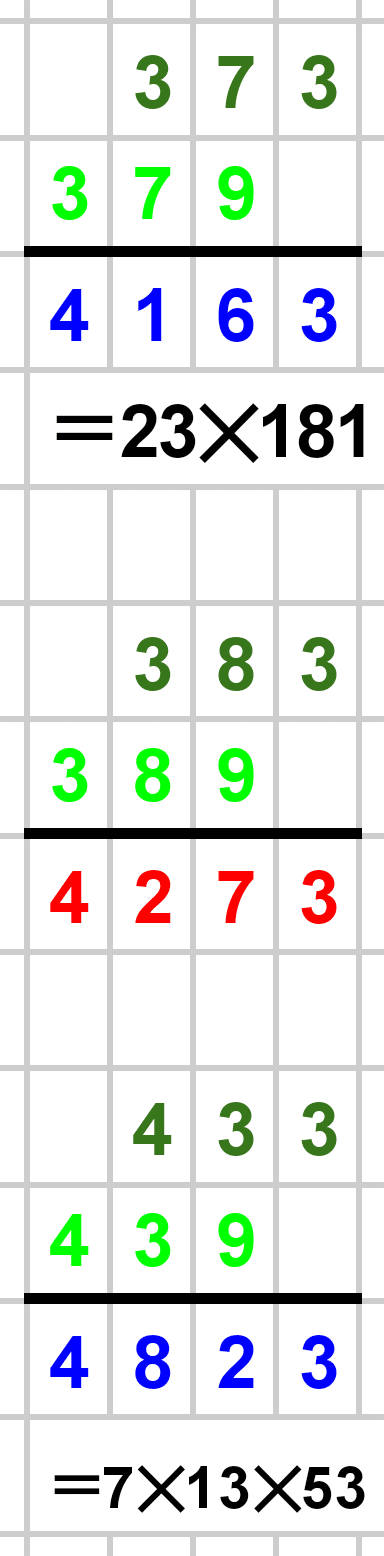
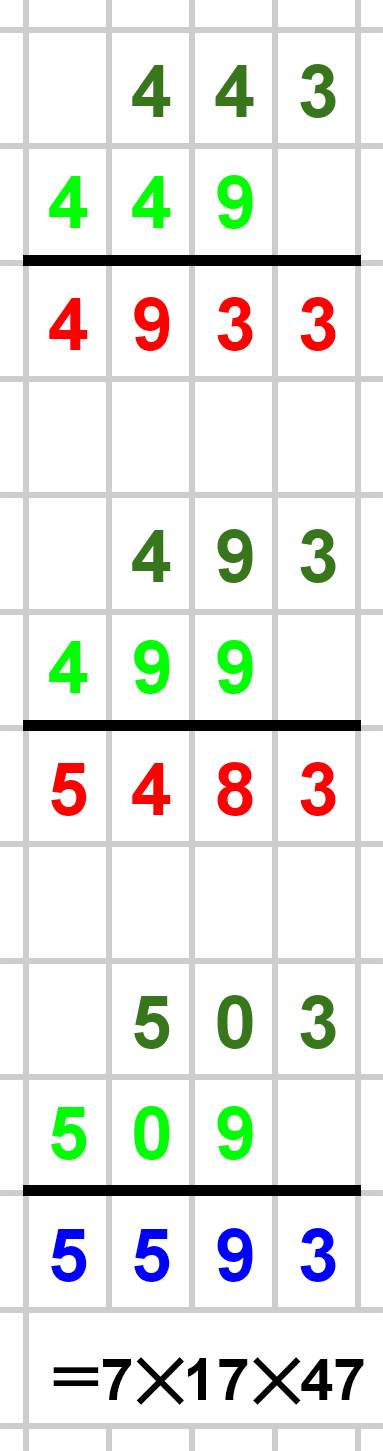
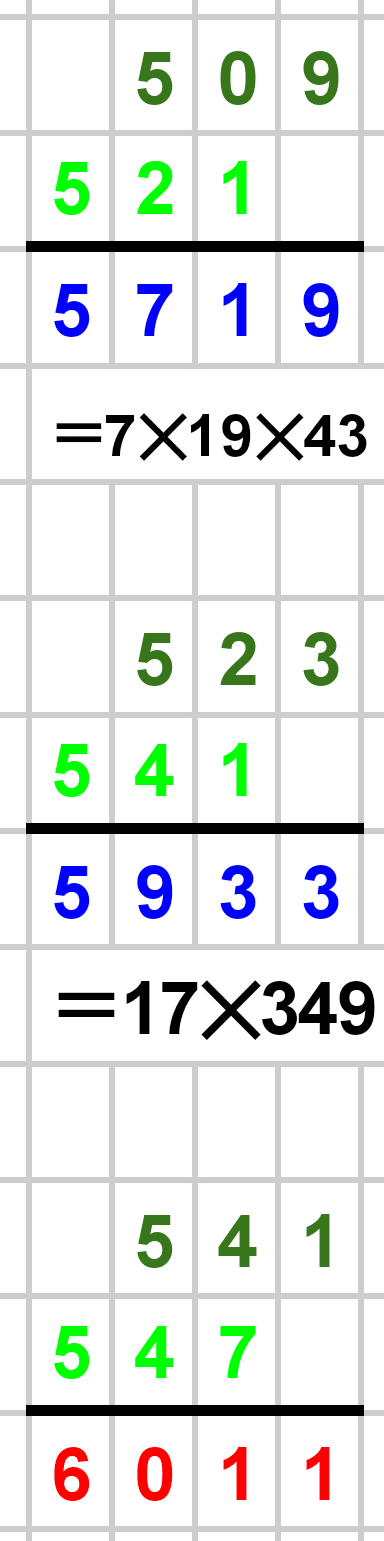
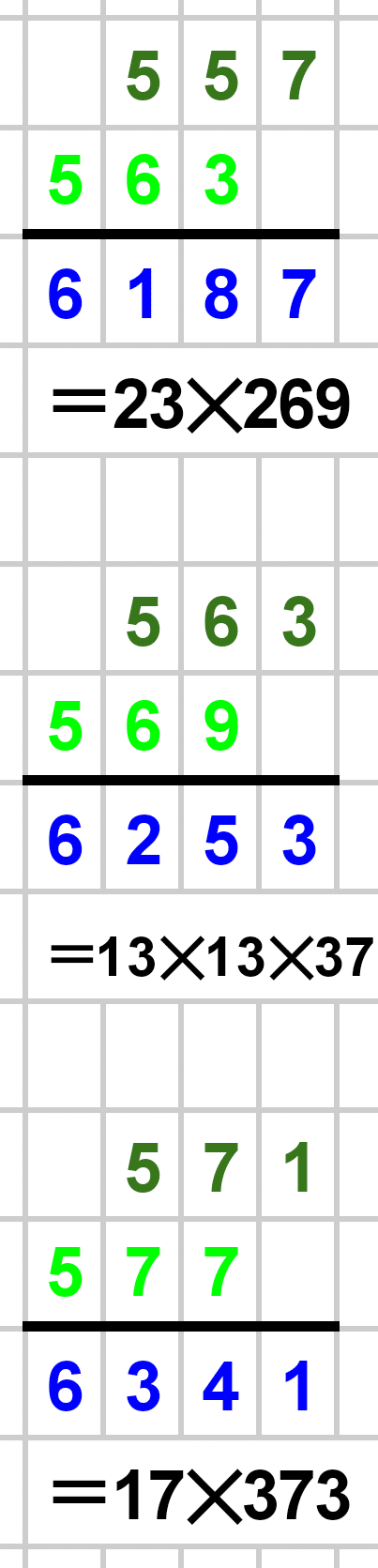
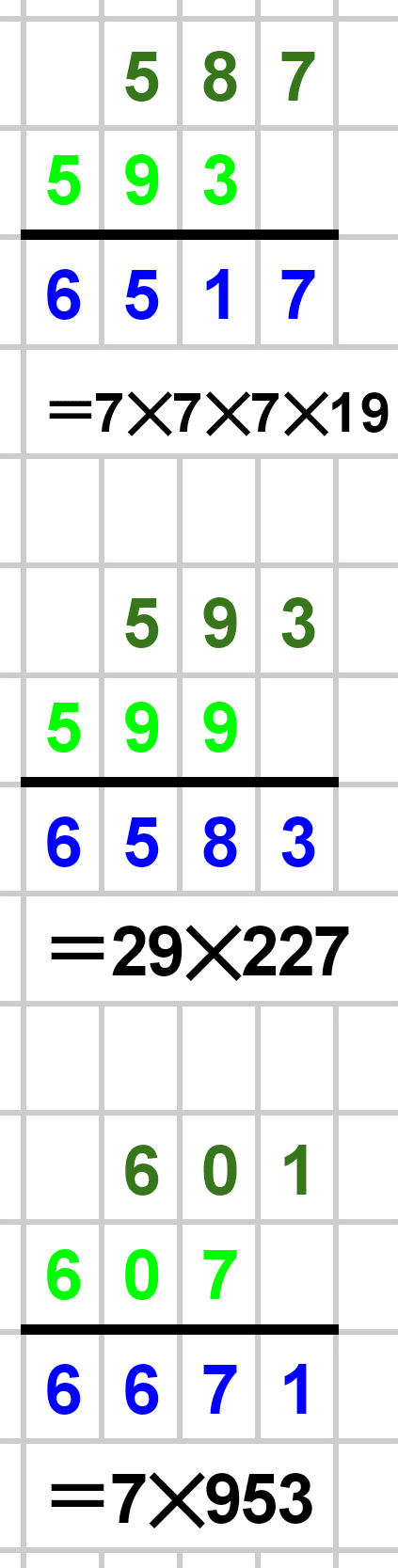
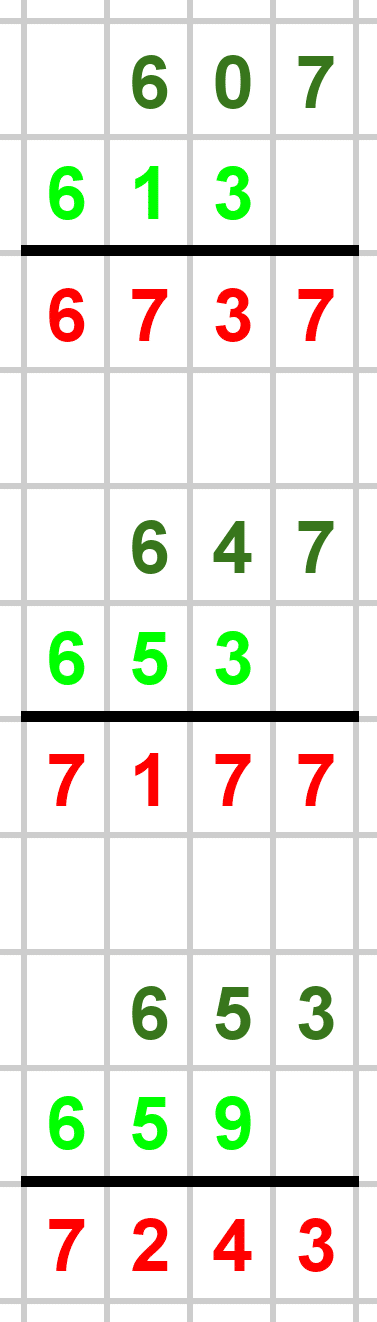
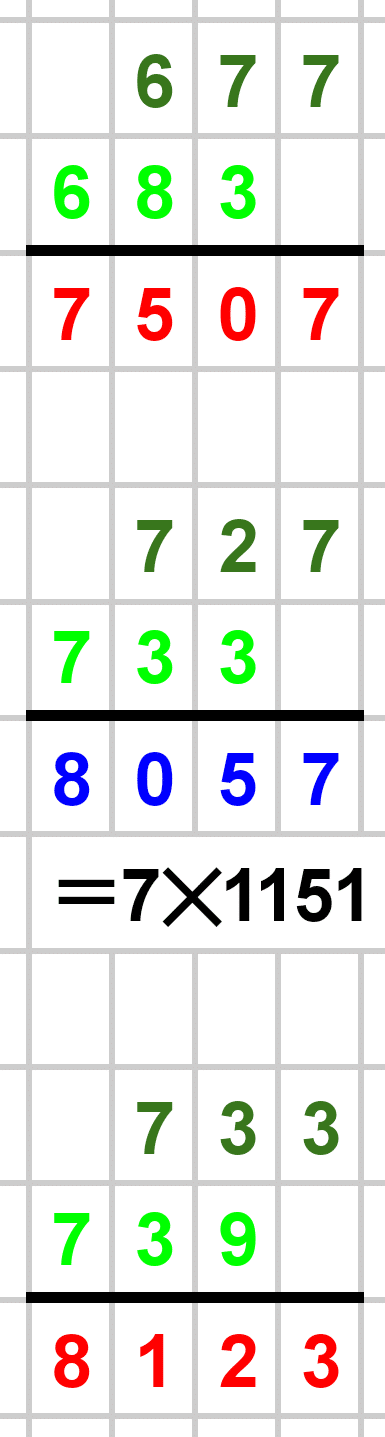
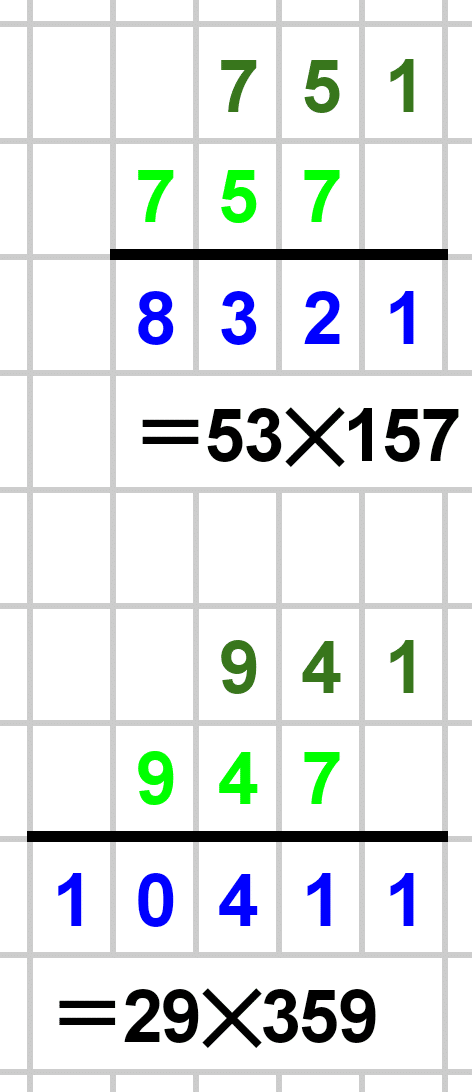
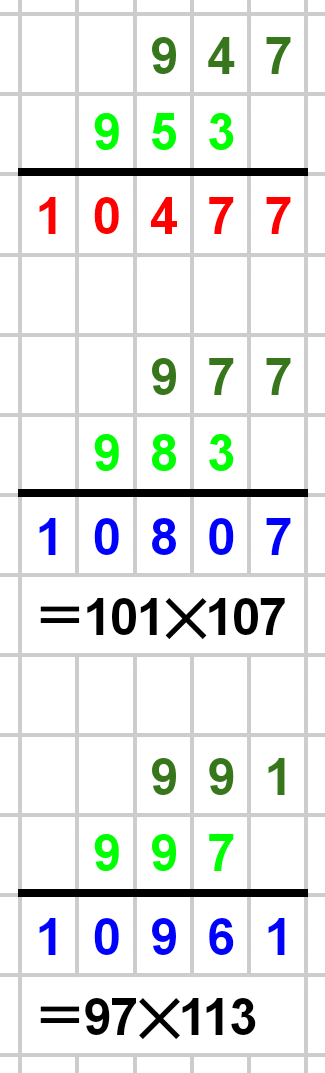
最後まで見ていただき、本当にありがとうございました！